- 2021-06-16 发布 |
- 37.5 KB |
- 4页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019届二轮复习几何变换法学案(全国通用)
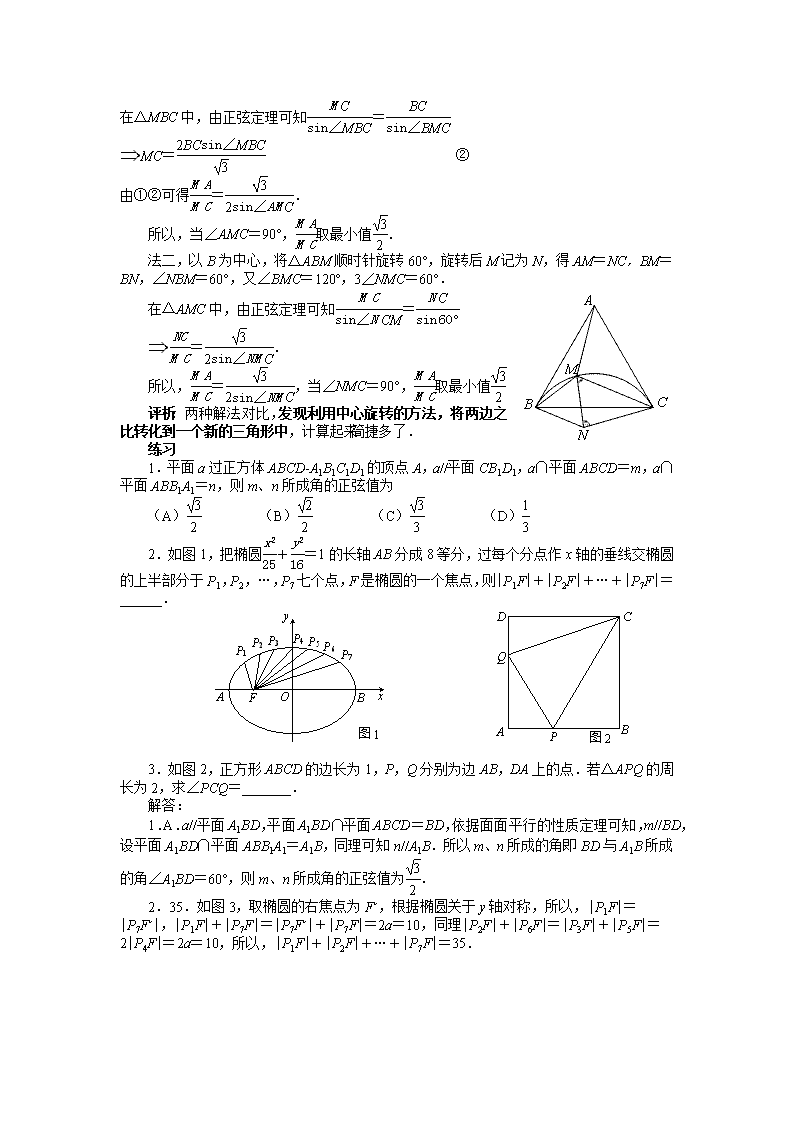
几何变换法在高中数学中的应用 高中数学中几何变换是全等变换,包括平移,轴对称,中心旋转,它们只改变图形的位置,不改变图形的形状与大小.几何变换法就是将图形的部分或全部变换到一个新的位置, 构成一个新的关系,有利于找出图形之间的关系,从而使解题更为简捷. 几何变换法常见于立体几何,解析几何,解三角形等问题中,几何变换法在这些知识的运用,对学生直观想象,数据处理能力提出较高的要求. 一. 平移变换(平行)在立体几何中的应用 例1.如图1,在棱长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在线段D1E上,点P到直线CC1的距离的最小值为________. C A D B1 A1 D1 B C1 P E C A D B1 A1 D1 B C1 P E P′ Q 图1 图2 分析:本题考察空间的距离问题,解决思路一,利用空间向量解决,建立空间直角坐标系,设出P点的坐标,求出P到直线CC1的距离,最后转化为函数求最小值.思路二,利用传统立体几何解题思路,把空间问题平面化.本题抓住过点P垂直直线CC1的直线与底面ABCD平行,在图2中,设点P在底面ABCD的射影P′,P′C即为点P到直线CC1的距离,从而把空间的距离转为平面ABCD内C到DE的距离. 解: 法一,以DA,DC,DD所在直线分别为x轴,y轴,z轴建立空间直角坐标系,设P的横坐标为x,则P的坐标(x,2x,2-2x),=(x,2x-2,2-2x),的同向向量m=(0,0,1). 设点P到直线CC1的距离为d, d2=||2sin2á,mñ=||2(1-cos2á,mñ)=||2-(•m)2 =x2+(2x-2)2+(2-2x)2-(2-2x)2 =5(x-)2+≥ 所以,点P到直线CC1的距离的最小值为. 法二,设点P在底面ABCD的射影P′,点P在直线CC1的射影为Q,连接P′C.由PQ∥平面ABCD,得PQ∥P′C,又PP′∥QC,所以四边形PP′CQ是平行四边形.P′C即为P到直线CC1的距离.因为在平面内直线外一点与直线上动点的连线中,垂线段最短,所以P′C⊥DE时,P′C==为最小值. 评析:两种解法,把空间问题平面化的解法不是空间向量法可代替的.线面平行与面面平行的性质定理,借助“确定平面”就是把空间的问题转化为平面问题的重要条件.而这种转化有事空间图形中解决部分问题的重要思想方法.这种转化最基本的依据就是四个公理.具体来讲,点P在线段D1E(不包括点E)上,PQ是变化的,不变的是PQ∥平面ABCD,过相交直线PQ,QC有唯一确定平面且与平面ABCD交于P′C,PQP′C,利用平移(平行)把空间问题转为平面问题. 二.轴对称在解析几何中的应用 例2.F是双曲线C:-=1(a>0,b>0)的右焦点,过点F向C的一条渐近线引 垂线,垂足为A,交另一条渐近线于点B.若2=,则C的离心率是______. 分析:本题考察双曲线的性质问题,思路一,把交点转化为方程组的解,把向量关系坐标化,最后联立方程组得到a,b的关系,进而求出离心率;思路二,利用双曲线的渐近线关于x轴对称,转化为平面几何问题. 解: 法一,不妨设直线AB的方程为y=-(x-c)与b2x2-a2y2=0联立得, (b4-a4)y2-2ab3cy+a2b2c2=0. y1+y2=, ① y1y2=, ② 2y1=-y2, ③ ①②③联立解得a2=3b2,所以e=. 法二,易知|FA|=b,|AB|=3b,设渐进线与x轴正半轴的夹角为α,则tanα=,tan2α=,于是=,整理得a2=3b2,所以e=. 法三,如右图,根据双曲线的对称性,过点F向C的另一条渐近线引垂线,垂足为C. 易知|FC|=b,|FB|=2b,在Rt△BFC中,得∠FBC=30°,所以∠AOB=60°,在Rt△AOF中,得∠AOF=30°, 所以e==. 评析:法一是几何问题直接代数化,求直线的交点,然后联立方程组得到a,b的关系,求离心率,此解法对数据处理能力,图形直观想象等思维能力体现层次较低;解法二着眼于对图形是双曲线的渐近线关于x轴对称的分析,抓住对称,还有|FA|=b,在直角三角形中结合二倍角公式得到a,b的关系,体现了学习与考试是一个厚积薄发的过程,此解法思维能力体现层次较好;解法三对解法二的改进,做出垂线段FC,利用双曲线的渐近线关于x轴对称,把条件转化到一个直角三角形中的解法让我们眼前一亮,此解法思维能力体现层次较高.圆锥曲线都是轴对称图形,有些问题抓住了对称,常觉意料之外,却在情理之中. 三.中心旋转在解三角形中的运用 例3.在等边△ABC中,M为△ABC内一动点,∠BMC=120º,则的最小值是_________. 分析:本题是在三角形中,求有关长度的最值问题,明确变量,利用正弦定理在相关的三角形表示出对应的边,然后建立比值的函数关系,求最值. 解: 法一由题意可知,∠MBC=∠ACM,在△AMC中,由正弦定理可知=ÞMA= ① 在△MBC中,由正弦定理可知= ÞMC= ② 由①②可得=. 所以,当∠AMC=90°,取最小值. 法二,以B为中心,将△ABM顺时针旋转60°,旋转后M记为N,得AM=NC,BM=BN,∠NBM=60°,又∠BMC=120º,3∠NMC=60°. 在△AMC中,由正弦定理可知= Þ=. 所以,=,当∠NMC=90°,取最小值 评析:两种解法对比,发现利用中心旋转的方法,将两边之比转化到一个新的三角形中,计算起来简捷多了. 练习 1.平面a过正方体ABCD-A1B1C1D1的顶点A,a//平面CB1D1,a∩平面ABCD=m,a∩平面ABB1A1=n,则m、n所成角的正弦值为 (A) (B) (C) (D) 2.如图1,把椭圆+=1的长轴AB分成8等分,过每个分点作x轴的垂线交椭圆的上半部分于P1,P2,…,P7七个点,F是椭圆的一个焦点,则|P1F|+|P2F|+…+|P7F|=______. A C B D Q P 图2 P1 P2 P3 P5 P4 P6 P7 A F B O x y 图1 3.如图2,正方形ABCD的边长为1,P,Q分别为边AB,DA上的点.若△APQ的周长为2,求∠PCQ=_______. 解答: 1.A.a//平面A1BD,平面A1BD∩平面ABCD=BD,依据面面平行的性质定理可知,m//BD,设平面A1BD∩平面ABB1A1=A1B,同理可知n//A1B.所以m、n所成的角即BD与A1B所成的角∠A1BD=60°,则m、n所成角的正弦值为. 2.35.如图3,取椭圆的右焦点为Fˊ,根据椭圆关于y轴对称,所以,|P1F|=|P7Fˊ|,|P1F|+|P7F|=|P7Fˊ|+|P7F|=2a=10,同理|P2F|+|P6F|=|P3F|+|P5F|=2|P4F|=2a=10,所以,|P1F|+|P2F|+…+|P7F|=35. P1 P2 P3 P5 P4 P6 P7 A F B O x y 图3 Fˊ A C B D Q P 图4 M 3.45°.以C为中心将△CDQ逆时针旋转90°,设旋转后的Q为M,∠PCM=90°.因为正方形ABCD的边长为1,△APQ的周长为2,所以QP=DQ+PB=BM+PB=PM,由QC=CM,则△CQP≌△CMP,故∠PCQ=∠PCQ=45°.查看更多