2017-2018学年广西宾阳县宾阳中学高二下学期3月月考数学（文）试题 Word版

2017-2018学年广西宾阳县宾阳中学高二下学期3月月考数学（文）试题 Word版

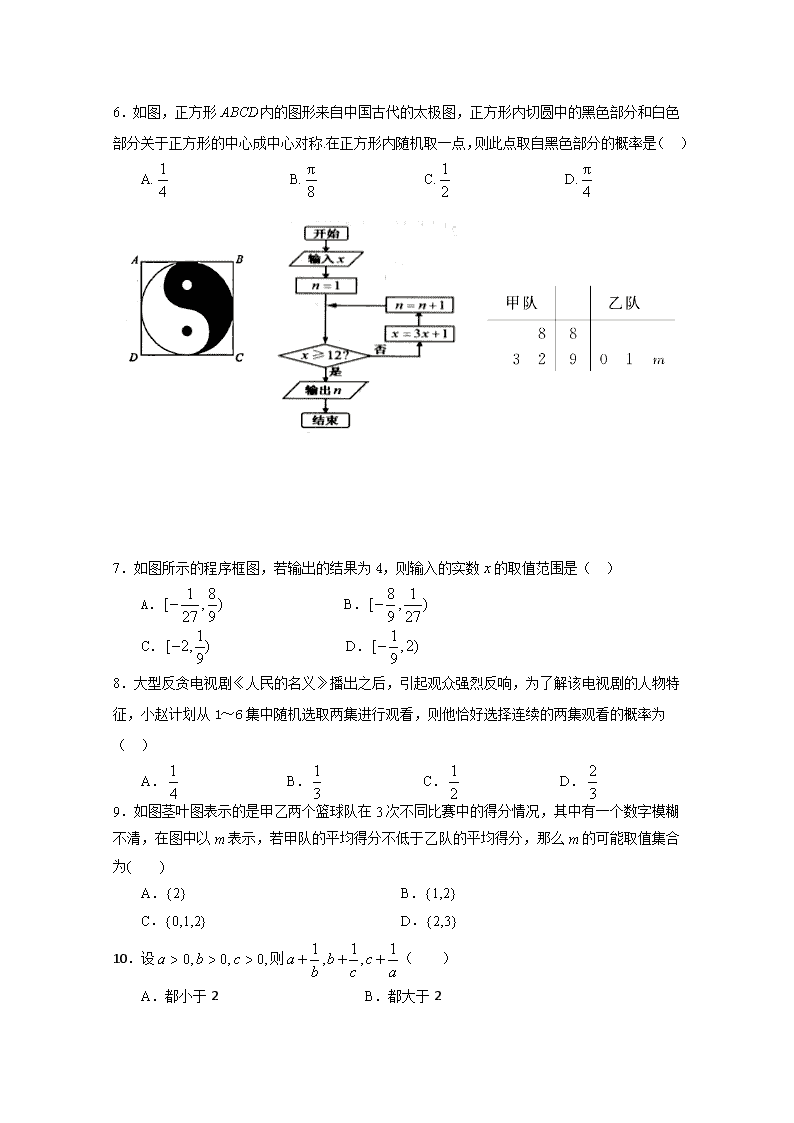
‎2017-2018学年广西宾阳县宾阳中学高二下学期3月月考数学（文） ‎ 出题人：赖盛芳 审题人：颜锡健 第Ⅰ卷（选择题 共60分）‎ 一、选择题：（本大题共12小题，每小题5分，共60分. 每小题四个选项中有且只有一个正确.）‎ ‎1．已知复数满足（为虚数单位），则等于（ ）‎ A． B． C． D．‎ ‎2．已知a＋b>0，b<0，那么a，b，－a，－b的大小关系是(　　)‎ A．a>－b>b>－a　　 B．a>－b>－a>b ‎ C．a>b>－b>－a D．a>b>－a>－b ‎3．函数f (x)在x = x0处导数存在，若p：f ′(x0) = 0：q：x = x0是f (x)的极值点，则（　　）‎ ‎ A． p是q的充分必要条件 ‎　 B． p是q的充分条件，但不是q的必要条件 ‎　 C． p是q的必要条件，但不是q的充分条件 D． p既不是q的充分条件，也不是q的必要条件 ‎4．采用系统抽样方法从960人中抽取32人做问卷调查，为此将他们随机编号为1,2，…，960，分组后在第一组采用简单随机抽样的方法抽到的号码为9.抽到的32人中，编号落入区间[1,450]的人做问卷A，编号落入区间[451,750]的人做问卷B，其余的人做问卷C，则抽到的人中，做问卷B的人数为(　　)‎ A．7　 B．9　 C．10　 D．15‎ ‎5．下列命题中：‎ ‎①线性回归方程必过点；‎ ‎②在回归方程中，当变量增加一个单位时，平均增加5个单位；‎ ‎③在回归分析中，相关指数为0.80的模型比相关指数为0.98的模型拟合的效果要好；‎ ‎④在回归直线中，变量时，变量的值一定是．‎ 其中假命题的个数是（ ）‎ A．1 B．2 C．3 D．4‎ ‎6．如图，正方形ABCD内的图形来自中国古代的太极图，正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点，则此点取自黑色部分的概率是（ ）‎ A. B. C. D.‎ ‎7．如图所示的程序框图，若输出的结果为4，则输入的实数的取值范围是（ ）‎ A． ‎ B． ‎ C. D．‎ ‎8．大型反贪电视剧《人民的名义》播出之后，引起观众强烈反响，为了解该电视剧的人物特征，小赵计划从1～6集中随机选取两集进行观看，则他恰好选择连续的两集观看的概率为（ ）‎ A． B． C． D．‎ ‎9．如图茎叶图表示的是甲乙两个篮球队在3次不同比赛中的得分情况，其中有一个数字模糊不清，在图中以m表示，若甲队的平均得分不低于乙队的平均得分，那么m的可能取值集合为(　　)‎ A．{2} B．{1,2}‎ C．{0,1,2} D．{2,3}‎ ‎10．设则（ ）‎ A．都小于2 B．都大于2‎ C. 至少有一个不大于2 D．至少有一个不小于2‎ ‎11．等轴双曲线C的中心在原点，焦点在x轴上，C与抛物线y2=16x的准线交于A，B两点，，则C的实轴长为（ ）‎ A．2 B． C．4 D．8‎ ‎12．若函数在上单调递增，则的取值范围是（ ）‎ A． B． C． D．‎ 第Ⅱ卷（非选择题 共90分）‎ 二、填空题：（本大题共4小题，每小题5分，共20分，把答案填在题中横线上）‎ ‎13．设命题：，，则为 .‎ ‎14．过抛物线的焦点作直线交抛物线于A，B两点，若线段AB的中点的横坐标为4，‎ 则等于 .‎ ‎15．从分别写有1，2，3，4，5的5张卡片中随机抽取1张，放回后再随机抽取1张，则抽得的第一张卡片上的数大于第二张卡片上的数的概率为 .‎ ‎16．不等式的解集为,则实数的取值范围是 .‎ 三、解答题：（本大题共6小题，共70分．解答应写文字说明，证明过程或演算步骤．）‎ ‎17．（本小题满分12分）‎ 在△ABC中，内角A，B，C的对边分别为a，b，c，且a2＝b2＋c2＋bc.‎ ‎(1)求A；‎ ‎(2)设a＝，S为△ABC的面积，求S＋3cos Bcos C的最大值，并求出此时B的值．‎ ‎18．（本小题满分12分）‎ 国家实施二孩放开政策后，为了了解人们对此政策持支持态度是否与年龄有关，计生部门将已婚且育有一孩的居民分成中老年组（45岁以上，含45岁）和中青年组（45岁以下，不含45岁）两个组别，每组各随机调查了50人，对各组中持支持态度和不支持态度的人所占的频率绘制成等高条形图，如图所示：‎ ‎（1）根据以上信息完成2×2列联表；‎ 支持 不支持 合计 中老年组 ‎50‎ 中青年组 ‎50‎ 合 计 ‎100‎ ‎（2）是否有99%以上的把握认为人们对此政策持支持态度与年龄有关？‎ P（K2≥k0）‎ ‎0.050‎ ‎0.010‎ ‎0.001‎ ‎ k0‎ ‎3.841‎ ‎6.635‎ ‎10.828‎ 附：．‎ ‎19．（本小题满分12分）‎ 已知函数f(x)＝ex(ax＋b)－x2－4x，曲线y＝f(x)在点(0，f(0))处的切线方程为y＝4x＋4．‎ ‎（1）求a，b的值；‎ ‎（2）讨论f(x)的单调性．‎ ‎20．（本小题满分12分）‎ 设F1 ，F2分别是椭圆C：（a>b>0）的左、右焦点，M是C上一点且MF2与x轴垂直，直线MF1与C的另一个交点为N.‎ ‎（1）若直线MN的斜率为，求C的离心率；‎ ‎（2）若直线MN在y轴上的截距为2且|MN|=5|F1N|，求a，b.‎ ‎21．（本小题满分12分）‎ 设a为实数，函数f(x)＝ex－2x＋2a，x∈R.‎ ‎(1)求f(x)的单调区间及极值；‎ ‎(2)求证：当a＞ln2－1且x＞0时，ex＞x2－2ax＋1.‎ 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.‎ ‎22．【选修4-5：坐标系与参数方程】（本小题满分10分）‎ 已知曲线的参数方程为(为参数),曲线的参数方程为(为参数)，‎ 且曲线与相交于两点.‎ ‎(1) 求曲线，的普通方程；‎ ‎(2) 若点，求的周长.‎ ‎23．【选修4-5：不等式选讲】（本小题满分10分）‎ 已知：是正实数，且.‎ ‎（1）求的最小值；‎ ‎（2）求证：.‎ 宾阳中学2018年春学期3月月考答案 ‎ 高二数学（文） ‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ B A C D C B A B C D C A 13. ‎， 14． 12 ‎ ‎15． 16．（-∞，-﹚‎ ‎17.解：(1)由余弦定理，得cos A＝＝＝－. -------------------2分 又∵0

查看更多