- 2021-06-15 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2013届高考数学一轮复习 三角函数的图象和性质
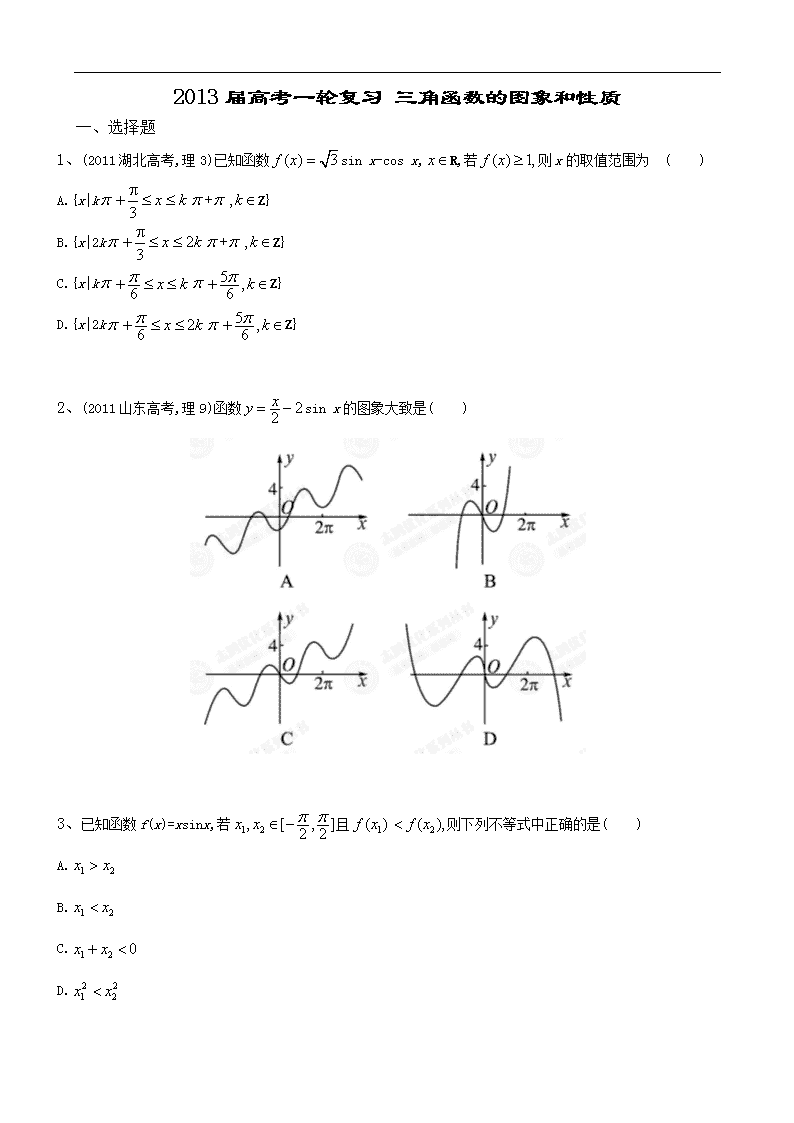
2013届高考一轮复习 三角函数的图象和性质 一、选择题 1、(2011湖北高考,理3)已知函数sin x-cos x,R,若则x的取值范围为 ( ) A.{x|k+Z} B.{x|2k+Z} C.{x|kZ} D.{x|2kZ} 2、(2011山东高考,理9)函数sin x的图象大致是( ) 3、已知函数f(x)=xsinx,若且则下列不等式中正确的是( ) A. B. C. D. 4、y=sinx-|sinx|的值域是( ) A.[-1,0] B.[0,1] C.[-1,1] D.[-2,0] 5、已知a是实数,则函数f(x)=1+asinax的图象不可能是( ) 6、已知函数f(x)=sinxcoscosxsin其中R,0<). (1)求函数f(x)的最小正周期; (2)若点在函数的图象上,求的值. 7、y=(sinx+cos是( ) A.最小正周期为2的偶函数 B.最小正周期为2的奇函数 C.最小正周期为的偶函数 D.最小正周期为的奇函数 8、函数y=sin)是R上的偶函数,则的值是( ) A.0 B. C. D. 9、已知函数f(x)=sin的图象关于直线对称,则可能是( ) A. B. C. D. 二、填空题 10、关于x的函数f(x)=cos有以下命题: ①对任意都是非奇非偶函数;②不存在使f(x)既是奇函数,又是偶函数;③存在使f(x)是偶函数;④对任意都不是奇函数. 其中一个假命题的序号是 ,因为当 时,该命题的结论不成立. 11、已知函数cosx,对于上的任意有如下条件: ①;②;③||. 其中能使恒成立的条件序号是 . 12、已知函数f(x)=ax+bsinx+1且f(5)=7,则f(-5)= . 13、若函数f(x)=2tan的最小正周期T满足1查看更多