空间几何体的结构特征(3课时)

空间几何体的结构特征(3课时)

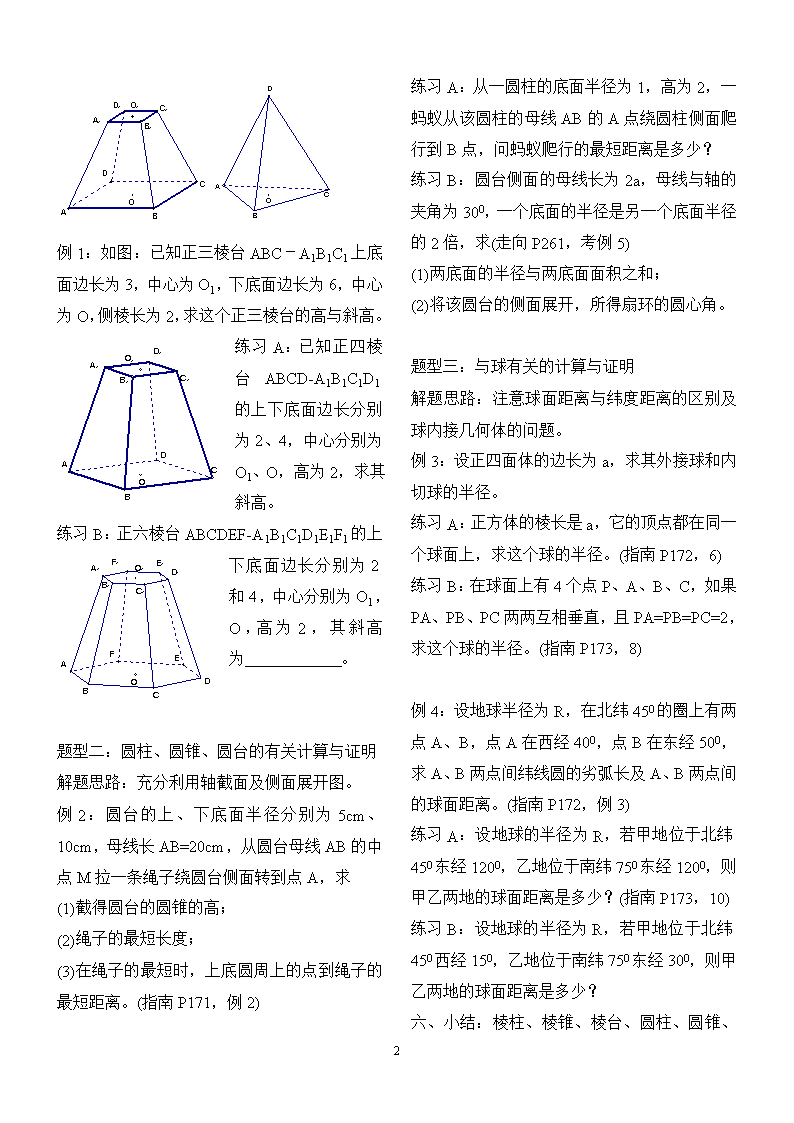
课题：空间几何体的结构特征(3课时)‎ 主备:邓立宏 审稿:张飞鹏 一、教学目的：‎ 认识柱、锥、台、球及其简单组合体的结构特征，并能运用这些特征描述现实生活中简单物体的结构。‎ 二、教学重点： 柱、锥、台、球的性质 三、教学难点：柱、锥、台、球性质应用 四、知识点归纳 ‎1、棱柱 ‎①定义：有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的几何体。 ‎ ‎②分类：按底面边数可分为：三棱柱、四棱柱等；按侧棱与底面是否垂直可分为：斜棱柱、直棱柱。‎ ‎③性质：侧棱都相等，侧面是平行四边形；两个底面与平行于底面的截面是全等的多边形；过不相邻的两条侧棱的截面是平行四边形。‎ ‎2、棱锥 ‎①定义：有一个面是多边形，其余各面都是有一个公共顶点的三角形，由这些面所围成的几何体。‎ ‎②正棱锥的定义：底面是正多边形，且各侧面全等的棱锥叫做正棱锥。性质：各侧棱相等，各侧面是全等的等腰三角形；棱锥的高、斜高和斜高在底面的射影组成一个直角三角形，棱锥的高、侧棱和侧棱在底面的射影组成一个直角三角形。‎ ‎3、棱台 ‎①定义：用一个平行于底面的平面去截棱锥，底面与截面之间的部分。‎ ‎②正棱台的定义：由正棱锥截得的棱台叫做正棱台。性质：各侧棱相等，各侧面是全等的等腰梯形；正棱台的两底面与平行于底面的截面是相似的正多边形；正棱台的两底面中心连线、相应的边心距和斜高组成一个直角梯形，两底面中心连线、侧棱和两底面相应半径也组成一个直角梯形。‎ ‎4、圆柱、圆锥、圆台 ‎①定义：分别以矩形的一边、直角三角形一直角边、直角梯形垂直于底边的腰所在的直线为旋转轴，其余各边旋转而形成的曲面所围成的几何体分别叫圆柱、圆锥、圆台。‎ ‎②性质：平行与底面的截面都是圆；轴截面分别是全等的矩形、等腰三角形、等腰梯形；侧面展开图分别是长方形、扇形、扇环。‎ ‎5、球 ‎①定义：以半圆的直径所在的直线为旋转轴，旋转所成的曲面。‎ ‎②球的截面性质：球心和截面圆心的连线垂直于截面；球心到截面的距离d与球的半径R及截面的半径r有下面关系：‎ ‎③球面距离的定义：在球面上，两点之间的最短距离，就是经过这两点的大圆在这两点间的一段劣弧的长度。‎ 三、典型题型及分层练习 题型一：正棱锥(台)中的有关计算与证明 解题思路：在解决有关正棱锥(台)中的有关计算与证明中，应作出与高、斜高、侧棱有关的直角三角形或直角梯形。‎ 3‎ 例1：如图：已知正三棱台ABC－A1B1C1上底面边长为3，中心为O1，下底面边长为6，中心为O，侧棱长为2，求这个正三棱台的高与斜高。‎ 练习A：已知正四棱台ABCD-A1B1C1D1的上下底面边长分别为2、4，中心分别为O1、O，高为2，求其斜高。‎ 练习B：正六棱台ABCDEF-A1B1C1D1E1F1的上下底面边长分别为2和4，中心分别为O1，O，高为2，其斜高为 。‎ 题型二：圆柱、圆锥、圆台的有关计算与证明 解题思路：充分利用轴截面及侧面展开图。‎ 例2：圆台的上、下底面半径分别为5cm、10cm，母线长AB=20cm，从圆台母线AB的中点M拉一条绳子绕圆台侧面转到点A，求 ‎(1)截得圆台的圆锥的高；‎ ‎(2)绳子的最短长度；‎ ‎(3)在绳子的最短时，上底圆周上的点到绳子的最短距离。(指南P171，例2)‎ 练习A：从一圆柱的底面半径为1，高为2，一蚂蚁从该圆柱的母线AB的A点绕圆柱侧面爬行到B点，问蚂蚁爬行的最短距离是多少？‎ 练习B：圆台侧面的母线长为2a，母线与轴的夹角为300，一个底面的半径是另一个底面半径的2倍，求(走向P261，考例5)‎ ‎(1)两底面的半径与两底面面积之和；‎ ‎(2)将该圆台的侧面展开，所得扇环的圆心角。‎ 题型三：与球有关的计算与证明 解题思路：注意球面距离与纬度距离的区别及球内接几何体的问题。‎ 例3：设正四面体的边长为a，求其外接球和内切球的半径。‎ 练习A：正方体的棱长是a，它的顶点都在同一个球面上，求这个球的半径。(指南P172，6)‎ 练习B：在球面上有4个点P、A、B、C，如果PA、PB、PC两两互相垂直，且PA=PB=PC=2，求这个球的半径。(指南P173，8)‎ 例4：设地球半径为R，在北纬450的圈上有两点A、B，点A在西经400，点B在东经500，求A、B两点间纬线圆的劣弧长及A、B两点间的球面距离。(指南P172，例3)‎ 练习A：设地球的半径为R，若甲地位于北纬450东经1200，乙地位于南纬750东经1200，则甲乙两地的球面距离是多少？(指南P173，10)‎ 练习B：设地球的半径为R，若甲地位于北纬450西经150，乙地位于南纬750东经300，则甲乙两地的球面距离是多少？‎ 3‎ 六、小结：棱柱、棱锥、棱台、圆柱、圆锥、圆台、球的性质 七、作业：《备考指南》P172 1---7题、9—10题 3‎