2018-2019学年黑龙江省鹤岗市第一中学高一下学期期末数学理科试题

2018-2019学年黑龙江省鹤岗市第一中学高一下学期期末数学理科试题

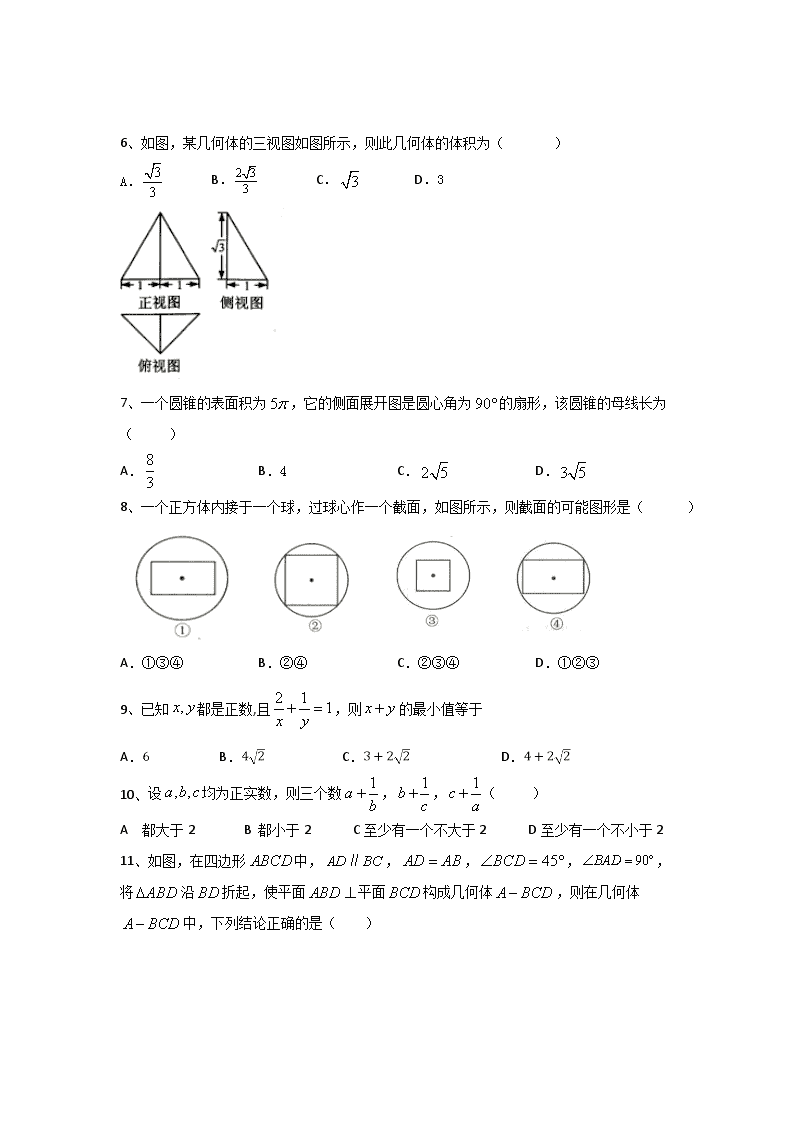
‎2018-2019学年黑龙江省鹤岗市第一中学高一下学期期末数学理科试题 一、选择题（本题共12题，每道题5分，共60分；每道小题只有一个符合题目要求）‎ ‎1、下列命题正确的是（ ）‎ A.有两个面平行，其余各面都是四边形的几何体叫棱柱。‎ B.有两个面平行，其余各面都是四边形，且每相邻两个四边形的公共边都互相平行的几何体叫棱柱。‎ C.绕直角三角形的一边旋转所形成的几何体叫圆锥。‎ D.用一个面去截棱锥，底面与截面之间的部分组成的几何体叫棱台。‎ ‎2、的斜二侧直观图如图所示，则的面积为（ ）‎ A． B．1 C． D．2 ‎ ‎3、如图，在直三棱柱中，,则异面直线与所成角的余弦值是（ ）‎ A. ‎ B. C. D. ‎ ‎ ‎ ‎4、已知，则的最小值是 （ ）‎ A．2 B．6 C．2 D．2‎ ‎5、若是不同的直线，是不同的平面，则下列命题中正确的是（ ）‎ A． 若，则 B．若，则 ‎.若则 D．若则 ‎6、如图，某几何体的三视图如图所示，则此几何体的体积为（ ）‎ A． ‎ B． C． D．3‎ ‎7、一个圆锥的表面积为，它的侧面展开图是圆心角为的扇形，该圆锥的母线长为（ ）‎ A． B．4 C． D．‎ ‎8、一个正方体内接于一个球，过球心作一个截面，如图所示，则截面的可能图形是（ ）‎ ‎ ‎ A．①③④ B．②④ C．②③④ D．①②③‎ ‎9、已知都是正数,且，则的最小值等于 A． B． C． D．‎ 10、 设均为正实数，则三个数，，（ ）‎ A 都大于2 B 都小于2 C至少有一个不大于2 D至少有一个不小于2 ‎ ‎11、如图，在四边形中，，，，，将沿折起，使平面平面构成几何体，则在几何体中，下列结论正确的是（ ）‎ A．平面平面 B．平面平面 C．平面平面 D．平面平面 ‎12、如图，已知四面体为正四面体，分别是中点.若用一个与直线垂直，且与四面体的每一个面都相交的平面去截该四面体，由此得到一个多边形截面，则该多边形截面面积最大值为（ ）.‎ A． B． C． D．‎ 二、填空题（本题共4个小题，每个小题5分，共20分）‎ ‎13、不等式的解集为_________________； ‎ ‎14、已知，且，则的最小值是 ．‎ ‎15、如图，二面角等于，、是棱上两点，、分别在半平面、内，，，且，则的长等于______．‎ 16、 已知三棱锥P－ABC，PA⊥平面ABC，AC⊥BC，PA＝2，AC＝BC＝1，‎ 则三棱锥P－ABC外接球的体积为 .‎ 三、 解答题（解答题应写出相应的文字说明，证明过程或验算步骤）‎ 17、 ‎（本题10分）‎ 的三个内角对应的三条边长分别，且满足．‎ ‎（Ⅰ）求角的大小；‎ ‎（Ⅱ）若，求．‎ 18、 ‎（本题12分）‎ 如图在四棱锥中，底面是矩形，点、分别是棱和的中点.‎ ‎（Ⅰ）求证：平面；‎ ‎（Ⅱ）若，且平面平面，证明平面.‎ 19、 ‎（本题12分）‎ 设数列的前项和为,已知 ‎（Ⅰ）求, 并求数列的通项公式；‎ ‎（Ⅱ）求数列的前项和．‎ 18、 ‎（本题12分）‎ 如图，四棱锥中，平面，底面是平行四边形，若，.‎ ‎（Ⅰ）求证：平面平面；‎ ‎（Ⅱ）求棱与平面所成角的正弦值.‎ 19、 ‎（本题12分）‎ 已知.‎ ‎（Ⅰ）求不等式的解集；‎ ‎（Ⅱ）若关于的不等式能成立，求实数的取值范围．‎ 20、 ‎（本题12分）‎ 如图，在四棱锥中，底面是直角梯形，侧棱底面，垂直于和，为棱上的点，，.‎ ‎（I）若为棱的中点，求证：//平；‎ ‎（II）当时，求平面与平面所成的锐二面角的余弦值；‎ ‎（III）在第（II）问条件下，设点是线段上的动点，与平面所成的角为，求当取最大值时点的位置.‎ 高一数学理科答案 一、选择题 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ B D D B C A B A C D A A 二、填空题 ‎13 14 ‎ ‎15 2 16 ‎ 三、 解答题 ‎17、解：⑴由正弦定理 得，--------------------------------------------------------------------------1分 ‎ 由已知得，，----------------------------------------------3‎ 因为，所以--------------------------------------------------------------5‎ ‎⑵由余弦定理，‎ 得 即，解得或，负值舍去，------------------------------9‎ 所以-----------------------------------------------------------------------------------------10‎ ‎18、‎ ‎（1）证明：因为点、分别是棱和的中点，所以，---------------------1‎ 又在矩形中，，所以，------------------------------------------2‎ 又面，------------------------------------------------------------------------------------3‎ 面，------------------------------------------------------------------------------------4‎ 所以平面------------------------------------------------------------------------------------5‎ （2） 证明：在矩形中，，又平面平面，‎ 平面平面，面，------------------------------------------7‎ 所以平面，---------------------------------------------------------------8‎ 又面，所以①---------------------------------------------------------------9‎ 因为且是的中点，所以，②------------------------------------------10‎ 由①②及面，面，，------------------------------------------11‎ 所以平面 .------------------------------------------------------------------------------------12‎ ‎19、解：（Ⅰ） 时 --------------------1‎ 所以时，------------3‎ 是首项为、公比为的等比数列，，．--------------------5‎ ‎（Ⅱ） ‎ ‎ ----------------------------------------8‎ 错位相减得: ‎ ‎ --------------------10‎ ‎．------------------------------------------------------------12‎ ‎20、解：‎ 解（Ⅰ）∵平面，平面∴，---------------------1‎ ‎∵，，，∴，∴，‎ ‎---------------------2‎ ‎∴平面，---------------------------------------------------------------3‎ 又∵平面，∴平面平面.---------------------------------------------------------------4‎ ‎（Ⅱ）以为原点，所在直线为轴，所在直线为轴，所在直线为轴，建立如图空间直角坐标系，则，，，，-----------------------------------------------6‎ 于是，，，-------------------------------------------7‎ 设平面的一个法向量为，则，解得，------------------9‎ ‎∴，--------------------------------------------------------11‎ 设与平面所成角为，则.----------------------------12‎ ‎21、解：（1）由题意可得|x﹣1|+|2x+3|＞4，‎ 当x≥1时，x﹣1+2x+3＞4，解得x≥1；------------------------------------------------------------1‎ 当时，1﹣x+2x+3＞4，解得0＜x＜1；----------------------------------------2‎ 当时，1﹣x﹣2x﹣3＞4，解得x＜﹣2．----------------------------------------3‎ 可得原不等式的解集为（﹣∞，﹣2）∪（0，+∞）；----------------------------------------4‎ ‎（2）由（1）可得，---------------------------------------------6‎ 可得时，|t﹣1|+|2t+3|取得最小值，----------------------------------------8‎ 关于x的不等式|x+l|﹣|x﹣m|≥|t﹣1|+|2t+3|（t∈R）能成立，‎ 等价为|x+l|﹣|x﹣m|的最大值，----------------------------------------9‎ 由|x+l|﹣|x﹣m|≤|m+1|，可得，----------------------------------------11‎ 解得或------------------------------------------------------------12‎ ‎22、解：（1）证明：取线段SC的中点E，连接ME，ED．‎ 在中，ME为中位线，∴， --------------------------------------------------------1‎ ‎∵，∴，∴四边形AMED为平行四边形．‎ ‎∴．------------------------------------------------------------------------------------2‎ ‎∵平面SCD，平面SCD，‎ ‎∴平面SCD．------------------------------------------------------------------------------------3‎ ‎（2）解：如图所示以点A为坐标原点，建立分别以AD、AB、AS所在的直线为x轴、y轴、z轴建立空间直角坐标系，则，，，，，----------------------------4‎ 由条件得M为线段SB近B点的三等分点．‎ 于是，即--------------------------------------------------------5‎ 设平面AMC的一个法向量为，则，‎ 将坐标代入得，--------------------------------------------------------7‎ 另外易知平面SAB的一个法向量为，‎ 所以平面AMC与平面SAB所成的锐二面角的余弦为．----------------------------8‎ ‎（3）设，其中．‎ 由于，所以．--------------------------------------------------------9‎ 所以，--------------------------------------------------------10‎ 可知当，即时分母有最小值，此时有最大值，----------------------------11‎ 此时，，即点N在线段CD上且．----------------------------12‎