- 2021-06-15 发布 |
- 37.5 KB |
- 44页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020_2021学年新教材高中数学第五章三角函数5
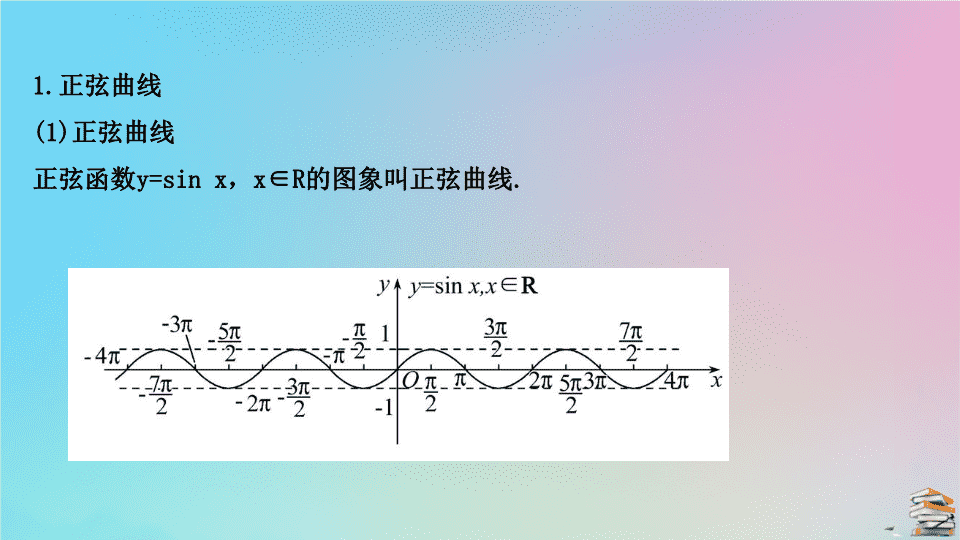
5.4.1 正弦函数、余弦函数的图象 必备知识 · 自主学习 1. 正弦曲线 (1) 正弦曲线 正弦函数 y=sin x , x∈R 的图象叫正弦曲线 . (2) 正弦函数图象的画法 ①几何法: (ⅰ) 利用正弦线画出 y=sin x , x∈[0 , 2π] 的图象; (ⅱ) 将图象向左、向右平行移动 ( 每次 2π 个单位长度 ). ②“ 五点法”: (ⅰ) 画出正弦曲线在 [0 , 2π] 上的图象的五个关键点 (0 , 0) , ______ , (π , 0) , _______ , (2π , 0) ,用光滑的曲线连接; (ⅱ) 将所得图象向左、向右平行移动 ( 每次 2π 个单位长度 ). (3) 本质:正弦曲线是正弦函数的图形表示,是正弦函数的一种直观表示 . (4) 应用:根据正弦曲线,能帮助学生更直观地认识正弦函数,进而根据正弦 曲线,推导正弦函数的一些常用性质 . 【 思考 】 在作 y=2+sin x 的图象时,应抓住哪些关键点? 提示: 作正弦函数 y=2+sin x , x∈[0 , 2π] 的图象时,起关键作用的点有以 下五个: (0 , 2) , , (π , 2) , , (2π , 2). 2. 余弦曲线 (1) 余弦曲线 余弦函数 y=cos x , x∈R 的图象叫余弦曲线 . (2) 余弦函数图象的画法 ①要得到 y=cos x 的图象,只需把 y=sin x 的图象向 ___ 平移 个单位长度即 可 . ② 用“五点法”画余弦曲线 y=cos x 在 [0 , 2π] 上的图象时,所取的五个关键 点分别为 (0 , 1) , , _________ , , _________ ,再用光滑的曲线 连接 . 左 (π , -1) (2π , 1) 【 思考 】 y=cos x(x∈R) 的图象可由 y=sin x(x∈R) 的图象平移得到的原因是什么? 提示: 因为 cos x=sin ,所以 y=sin x(x∈R) 的图象向左平移 个单位 长度可得 y=cos x(x∈R) 的图象 . 【 基础小测 】 1. 辨析记忆 ( 对的打“√”,错的打“ ×”) (1)“ 五点法”作正、余弦函数的图象时的“五点”是指图象上的任意五 点 .( ) (2) 余弦函数 y=cos x 的图象与 y=sin x 的图象形状和位置都不一样 .( ) (3) 函数 y=sin x 与 y=sin(-x) 的图象完全相同 . ( ) 提示: (1)×. 取的五个点的横坐标分别为 0 , , π , π , 2π. (2)×. 函数 y=cos x 的图象与 y=sin x 的图象形状一样,只是位置不同 . (3)×. 二者图象不同,关于 x 轴对称 . 2. 以下对正弦函数 y=sin x 的图象描述不正确的是 ( ) A. 在 x∈[2kπ , 2(k+1)π](k∈Z) 上的图象形状相同,只是位置不同 B. 介于直线 y=1 与直线 y=-1 之间 C. 关于 x 轴对称 D. 与 y 轴仅有一个交点 【 解析 】 选 C. 画出 y=sin x 的图象 ( 图略 ) ,根据图象可知 A , B , D 三项都正确 . 3.( 教材二次开发:例题改编 ) 函数 y=-xcos x 的部分图象是 ( ) 【 解析 】 选 D. 因为 y=-xcos x 是奇函数,它的图象关于原点对称,所以排除 A , C 项;当 x∈ 时, y=-xcos x<0 ,所以排除 B 项 . 关键能力 · 合作学习 类型一 正弦函数、余弦函数图象的初步认识 ( 数学抽象 ) 【 题组训练 】 1. 用“五点法”作 y=sin 2x 的图象时,首先描出的五个点的横坐标是 ( ) A.0 , , π , , 2π B.0 , , , , π C.0 , π , 2π , 3π , 4π D.0 , , , , 2. 下列图象中,是 y=-sin x 在 [0 , 2π] 上的图象的是 ( ) 3. 下列函数图象相同的是 ( ) A.f(x)=sin x 与 g(x)=sin(π+x) B.f(x)=sin 与 g(x)=sin C.f(x)=sin x 与 g(x)=sin(-x) D.f(x)=sin(2π+x) 与 g(x)=sin x 【 解析 】 1. 选 B. 分别令 2x=0 , , π , , 2π ,可 x=0 , , , , π. 2. 选 D. 函数 y=-sin x 的图象与函数 y=sin x 的图象关于 x 轴对称 . 3. 选 D.A 中 g(x)=-sin x ; B 中 f(x)=-cos x , g(x)=cos x ; C 中 g(x)=-sin x ; D 中 f(x)=sin x. 【 解题策略 】 利用正弦、余弦函数图象解题 (1) 熟练掌握正余弦函数的图象,必要时用“五点法”作出图象观察 . (2) 熟练应用诱导公式变形,通过函数解析式的关系确定图象关系 . (3) 掌握常见的图象变换,如 -f(x) , f(-x) , f(|x|) 等 . 【 补偿训练 】 函数 y=sin |x| 的图象是 ( ) 【 解析 】 选 B.y=sin |x|= 故选 B. 类型二 用“五点法”作三角函数的图象 ( 直观想象 ) 【 典例 】 用“五点法”作出下列函数的简图 . (1)y=1-sin x(0≤x≤2 π ) ; (2)y=2+cos x , x∈[0 , 2 π ]. 【 思路导引 】 求作三角函数的图象,需要先列表,再描点,最后用平滑曲线连线 . 【 解析 】 (1)① 列表: ② 描点连线,如图所示 . (2)① 列表: ② 描点连线,如图所示 . 【 解题策略 】 “ 五点法”画函数 y=Asin x+b(A≠0) 在 [0 , 2π] 上的简图的步骤 (1) 列表 (2) 描点:在平面直角坐标系中描出下列五个点: (0 , y 1 ) , , (π , y 3 ) , , (2π , y 5 ). (3) 连线:用光滑的曲线将描出的五个点连接起来 . 【 跟踪训练 】 请补充完整下面用“五点法”作出 y=-sin x(0≤x≤2π) 图象的列表 . ①_______ ;② _______ ;③ _______. 【 解析 】 用 “ 五点法 ” 作 y=-sin x(0≤x≤2π) 的图象的五个关键点为 (0 , 0) , , (π , 0) , , (2π , 0) ,故①为 π ,②为 0 ,③为 1. 答案: ① π ② 0 ③ 1 类型三 正弦、余弦函数图象的应用 ( 逻辑推理 ) 角度 1 零点个数问题 【 典例 】 在同一坐标系中,作函数 y=sin x 和 y=lg x 的图象,根据图象判断出方程 sin x=lg x 的解的个数 . 【 解析 】 建立平面直角坐标系 xOy ,先用五点法画出函数 y=sin x , x∈R 的图 象 . 描出点 (1 , 0) , (10 , 1) ,并用光滑曲线连接得到 y=lg x 的图象,如图所示 . 由图象可知方程 sin x=lg x 的解有 3 个 . 【 变式探究 】 根据函数图象求方程根的个数问题,是常见的考查模式;将典例中问题改 为:方程 sin x= 的根的个数是 ( ) A.7 B.8 C.9 D.10 【 解析 】 选 A. 在同一坐标系内画出 y= 和 y=sin x 的图象如图所示 . 根据图象可知方程有 7 个根 . 角度 2 利用正、余弦函数的图象解不等式 【 典例 】 在 [0 , 2π] 内,不等式 2sin x-1≥0 的解集为 ( ) A. B. C. D. 【 思路导引 】 在 [0 , 2π] 上,作出 y=sin x 的图象,再在这个平面直角坐标系 中作出直线 y= ,观察图象,找到满足 sin x≥ 的 x 的取值范围 . 【 解析 】 选 D. 因为 2sin x-1≥0 ,所以 sin x≥ . 在同一坐标系下,作函数 y=sin x , x∈[0 , 2π] 的图象以及直线 y= . 由函数的图象知, sin =sin π= . 所以根据图象可知, sin x≥ 的解集为 【 解题策略 】 用三角函数图象解三角不等式的步骤 (1) 作出正弦函数在 [0 , 2π] 或 的图象,余弦函数在 [0 , 2π] 或 [-π , π] 上的图象 . (2) 写出适合不等式在给定区间上的解集 . 【 题组训练 】 1. 方程 x 2 -cos x=0 的实数解的个数为 ( ) A.1 B.2 C.3 D.4 2. 使不等式 -2sin x≥0 在 [-π , π] 上成立的 x 的取值范围是 ( ) A. B. C. ∪ D. 3. 在 (0 , 2π) 内,使 sin x>cos x 成立的 x 的取值范围是 _______. 【 解析 】 1. 选 B. 作函数 y=cos x 与 y=x 2 的图象,如图所示, 由图象可知,原方程有两个实数解 . 2. 选 C. 不等式可化为 sin x≤ . 作图,正弦曲线及直线 y= 如图所示 . 又 x∈[-π , π] ,结合图象可知 x 的解集为 3. 在同一坐标系中画出 y=sin x , x∈(0 , 2π) 与 y=cos x , x∈(0 , 2π) 的图 象如图所示, 由图象可观察出当 x∈ 时, sin x>cos x. 答案: 【 补偿训练 】 y=1+sin x , x∈[0 , 2π] 的图象与直线 y= 交点的个数是 ( ) A.0 B.1 C.2 D.3 【 解析 】 选 C. 用 “ 五点法 ” 作出函数 y=1+sin x , x∈[0 , 2π] 的图象,作出 直线 y= 的图象如图所示, 由图可知,这两个函数的图象有 2 个交点 . 1. 用“五点法”画函数 y=2-3sin x 的图象时,首先应描出五点的横坐标是 ( ) A.0 , , , , π B.0 , , π , , 2π C.0 , π , 2π , 3π , 4π D.0 , , , , 【 解析 】 选 B. 所描出的五点的横坐标与函数 y=sin x 的五点的横坐标相同,即 0 , , π , , 2π ,故选 B. 课堂检测 · 素养达标 2. 函数 y=cos x 与函数 y=-cos x 的图象 ( ) A. 关于直线 x=1 对称 B. 关于原点对称 C. 关于 x 轴对称 D. 关于 y 轴对称 【 解析 】 选 C. 由解析式可知 y=cos x 的图象过点 (a , b) ,则 y=-cos x 的图象必过点 (a , -b) ,由此推断两个函数的图象关于 x 轴对称 . 3.( 教材二次开发:练习改编 ) 在同一平面直角坐标系内,函数 y=sin x , x∈[0 , 2π] 与 y=sin x , x∈[2π , 4π] 的图象 ( ) A. 重合 B. 形状相同,位置不同 C. 关于 y 轴对称 D. 形状不同,位置不同 【 解析 】 选 B. 根据正弦曲线的作法可知函数 y=sin x , x∈[0 , 2π] 与 y= sin x , x∈[2π , 4π] 的图象只是位置不同,形状相同 . 4. 如图是下列哪个函数的图象 ( ) A.y=1+sin x , x∈[0 , 2π] B.y=1+2sin x , x∈[0 , 2π] C.y=1-sin x , x∈[0 , 2π] D.y=1-2sin x , x∈[0 , 2π] 【 解析 】 选 C. 把 这一点代入选项检验,即可排除 A 、 B 、 D. 5. 在 [0 , 2π] 内,不等式 sin x<- 的解集是 ( ) A.(0 , π) B. C. D. 【 解析 】 选 C. 画出 y=sin x , x∈[0 , 2π] 的图象如图: 因为 sin = ,所以 sin =- , sin =- . 即在 [0 , 2π] 内,满足 sin x=- 的是 x= 或 x= . 可知不等式 sin x<- 的解集是 . 核心知识 方法总结 易错提醒 核心素养 正弦函数的图象 几何法 五点法 余弦函数的图象 平移法 五点法 利用五点法作图:( 1 )列表;( 2 )描点;( 3 )画图 正、余弦曲线形状相同,位置不同 直观想象:通过正、余弦函数图象的运用,培养直观想象的核心素养 正弦函数、余 弦函数的图象查看更多