2017-2018学年四川省广安市高二上学期第三次月考数学理试题 无答案（Word版）

2017-2018学年四川省广安市高二上学期第三次月考数学理试题 无答案（Word版）

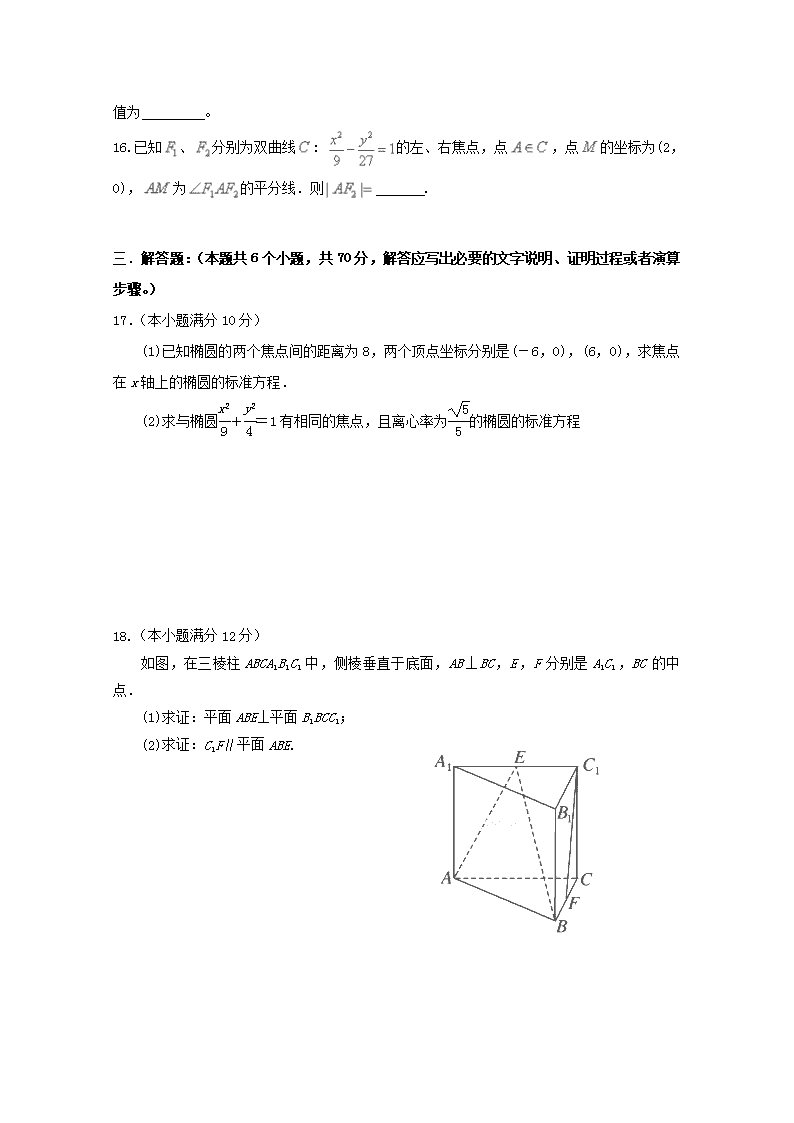
四川省广安市2017-2018学年高二数学上学期第三次月考试题 理（无答案）‎ 注意事项：‎ ‎1．本试卷满分为150分，考试时间为120分钟。‎ ‎2.答题前，考生先将自己的姓名、准考证号码填写清楚；‎ ‎3.选择题必须使用2B铅笔填涂, 非选择题必须使用0.5毫米黑色的签字笔书写, 字迹清楚；‎ ‎4.请在各题目的答题区域内作答，超出答题区域书写的答案无效，在草稿纸上答题无效；‎ ‎5.保持卡面清洁，不得折叠、不要弄破、弄皱，不准使用涂改液、刮纸刀 一、选择题（本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.）‎ ‎1．在直角坐标系中，直线的倾斜角是（　　）‎ A． B． C． D．不存在 ‎2．直线3x+y+1=0和直线6x+2y+1=0的位置关系是（   ） ‎ A．重合 B．垂直 C．平行 D．相交但不垂直 ‎3、若椭圆＋＝1上一点P到焦点F1的距离为6，则点P到另一焦点F2的距离是(　　)‎ A．2　　　　 B．4 C．6 D．8‎ ‎4.已知双曲线：的离心率，且其右焦点，则双曲线的方程为（ ）‎ A. B. C． D. ‎ ‎5．在等比数列中，，则数列的前项的和 ‎（ ）‎ A.255 B.256 C.511 D.512‎ ‎6．直线被圆所截得的弦长为（ ）‎ A． B． C． D．‎ ‎7．椭圆的短轴的一个顶点与两焦点组成等边三角形，则它的离心率为(　 　)‎ A. B. C. D. ‎8.“”是“”的（ ）‎ A.充要条件 B.必要不充分条件 C.充分不必要条件 D.既不充分也不必要条件 ‎9.已知两个不同的平面、和两个不重合的直线、，有下列四个命题：‎ ‎①若，，则； ②若，则；‎ ‎③若，，则；④若，则，‎ 其中真命题的个数是（ ）‎ A. B. C. D. ‎ ‎10.如图，在直三棱柱ABC－A1B1C1中，∠ABC＝，D是棱AC的中点，且AB＝BC＝BB1＝2.求异面直线AB1与BC1所成的角( )‎ A. B. C. D. ‎11．下列命题中是假命题的是(　　)‎ A．∃m∈R，使是幂函数，且在(0，＋∞)上单调递减 B．∀a>0，函数f(x)＝ln2x＋lnx－a有零点 C．∃α，β∈R，使cos(α＋β)＝cosα＋sinβ D．∀φ∈R，函数f(x)＝sin(2x＋φ)都不是偶函数 ‎12．已知动直线恒过点P（1，m），且Q（4，0）到动直线的最大距离为3，则的最小值为（　　）‎ A．1 B． C． D．9‎ 二、 填空题：本大题共4小题，每小题5分，共20分。把答案填在答题卡相应位置。‎ ‎13．空间直角坐标系中，点A（﹣3，4，0）与点B（x，﹣1，6）的距离为，则等于 ______．‎ ‎14．设点P是双曲线－＝1上任意一点，F1，F2分别是其左、右焦点，若|PF1|＝10，则|PF2|＝________．‎ ‎15．已知点P是椭圆上任一点，则点P到直线：的距离的最小值为 。‎ ‎16.已知、分别为双曲线: 的左、右焦点，点，点的坐标为(2，0)，为的平分线．则 .‎ 三．解答题：（本题共6个小题，共70分，解答应写出必要的文字说明、证明过程或者演算步骤。）‎ ‎17．（本小题满分10分）‎ ‎(1)已知椭圆的两个焦点间的距离为8，两个顶点坐标分别是(－6，0)，(6，0)，求焦点在x轴上的椭圆的标准方程．‎ ‎(2)求与椭圆＋＝1有相同的焦点，且离心率为的椭圆的标准方程 ‎18.（本小题满分12分）‎ 如图，在三棱柱ABCA1B1C1中，侧棱垂直于底面，AB⊥BC，E，F分别是A1C1，BC的中点．‎ ‎(1)求证：平面ABE⊥平面B1BCC1；‎ ‎(2)求证：C1F∥平面ABE.‎ ‎19．（本小题满分12分）‎ 已知命题：方程所表示的曲线为焦点在y轴上的椭圆；命题：实数满足不等式. ‎ ‎（1）若命题为真，求实数的取值范围；‎ ‎（2）若命题是命题的充分不必要条件，求实数的取值范围．‎ ‎20．（本小题满分12分）‎ 已知以点P为圆心的圆经过点A(－1,0)和B(3,4)，线段AB的垂直平分线交圆P于点C和D，且|CD|＝4.‎ ‎(1)求直线CD的方程；‎ ‎(2)求圆P的方程．‎ ‎21. （本小题满分12分）‎ 已知数列 的前n项和Sn=3n2+8n，是等差数列，且 ‎ ‎（1）求数列的通项公式；‎ ‎（2）令 求数列的前n项和Tn.‎ ‎22.（本小题满分12分）‎ 已知动点到直线的距离是它到点的距离的倍.‎ ‎（1）求动点的轨迹的方程；‎ ‎（2）过点的直线与轨迹交于两点，若是的中点，求直线的率.‎