【数学】2018届一轮复习人教A版第4章第1节平面向量的概念及线性运算学案

【数学】2018届一轮复习人教A版第4章第1节平面向量的概念及线性运算学案

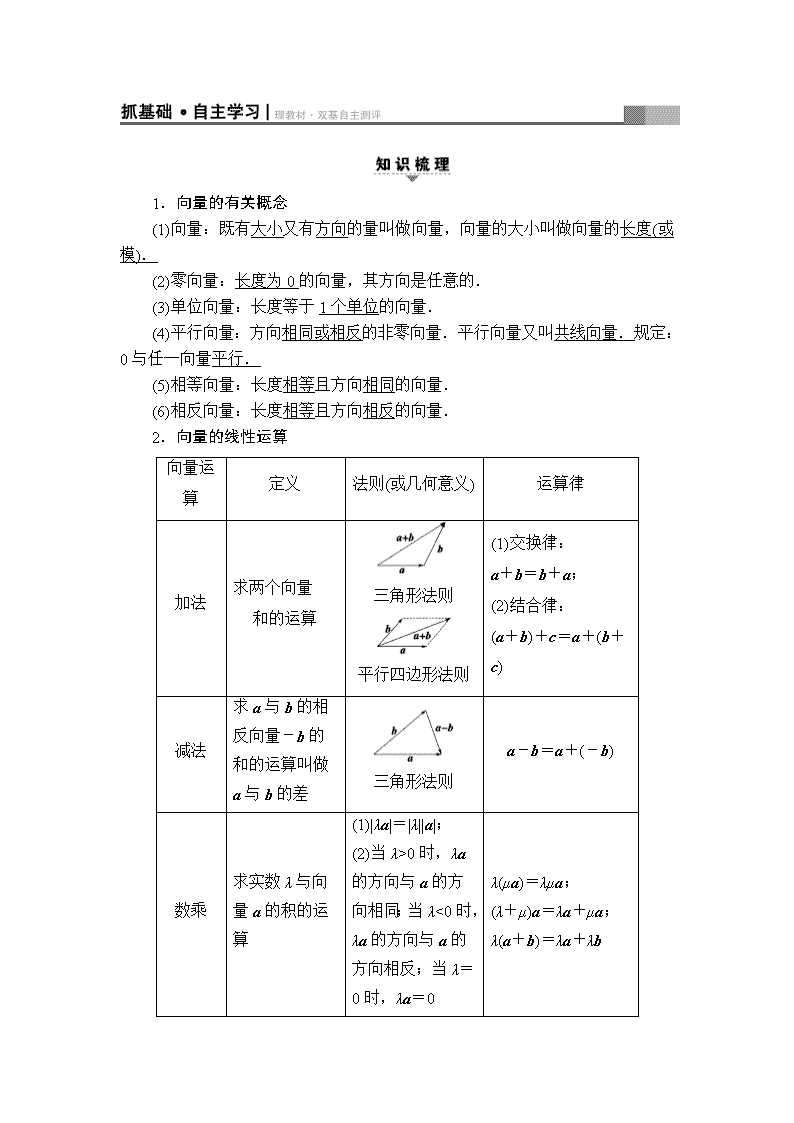
第四章 平面向量、数系的扩充与复数的 引入 [深研高考·备考导航] 为教师备课、授课提供丰富教学资源 [五年考情] 考点 2016 年 2015 年 2014 年 2013 年 2012 年 平面向量的 线性运算 8,5 分(理) 17,4 分(理) 5,5 分(理) 15,4 分(理) 平面向量的 基本定理及 坐标表示 13,4 分 (文) 7,5 分(理) 平面向量的 数量积 15,4 分(理) 15,4 分(文) 13,4 分 (文) 8,5 分(理) 9,5 分(文) 17,4 分(理) 5,5 分(理) 15,4 分(理) 向量的综合 应用 15,4 分(文) 15,4 分(理) 7,5 分(理) 7,5 分(文) 复数的概念 及运算 2,5 分(理) 11,4 分 (文) 1,5 分(理) 2,5 分(文) 2,5 分(理) 2,5 分(文) [重点关注] 从近五年浙江高考试题来看，平面向量与复数是每年的必考内容．主要考查 平面向量的线性运算，平面向量共线与垂直的充要条件，平面向量的数量积及其 应用复数的有关概念及复数代数形式的四则运算，多以客观题的形式出现，难度 以容易题为主． 第一节 平面向量的概念及线性运算 1．向量的有关概念 (1)向量：既有大小又有方向的量叫做向量，向量的大小叫做向量的长度(或 模)． (2)零向量：长度为 0 的向量，其方向是任意的． (3)单位向量：长度等于 1 个单位的向量． (4)平行向量：方向相同或相反的非零向量．平行向量又叫共线向量．规定： 0 与任一向量平行． (5)相等向量：长度相等且方向相同的向量． (6)相反向量：长度相等且方向相反的向量． 2．向量的线性运算 向量运 算 定义 法则(或几何意义) 运算律 加法 求两个向量 和的运算 三角形法则 平行四边形法则 (1)交换律： a＋b＝b＋a； (2)结合律： (a＋b)＋c＝a＋(b＋ c) 减法 求a与b的相反 向量－b 的和 的运算叫做 a 与 b 的差 三角形法则 a－b＝a＋(－b) 数乘 求实数λ与向量 a 的积的运算 (1)|λa|＝|λ||a|； (2)当λ>0 时，λa 的 方向与a的方向相 同；当λ<0 时，λa λ(μa)＝λμa； (λ＋μ)a＝λa＋μa； λ(a＋b)＝λa＋λb 的方向与a的方向 相反；当λ＝0 时， λa＝0 3.共线向量定理 向量 a(a≠0)与 b 共线的充要条件是存在唯一一个实数λ，使得 b＝λa. 1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”) (1)向量与有向线段是一样的，因此可以用有向线段来表示向量．( ) (2)若 a∥b，b∥c，则 a∥c.( ) (3)a∥b 是 a＝λb(λ∈R)的充要条件．( ) (4)△ABC 中，D 是 BC 的中点，则AD → ＝1 2(AC →＋AB → )．( ) [答案] (1)× (2)× (3)× (4)√ 2．设 D 为△ABC 所在平面内一点，BC →＝3CD → ，则( ) A.AD → ＝－1 3AB →＋4 3AC → B.AD → ＝1 3AB →－4 3AC → C.AD → ＝4 3AB →＋1 3AC → D.AD → ＝4 3AB →－1 3AC → A [AD → ＝AC → ＋CD → ＝AC → ＋1 3BC → ＝AC → ＋1 3(AC → －AB → )＝4 3AC → －1 3AB → ＝－1 3AB → ＋ 4 3AC → .故选 A.] 3．(2017·绍兴质检)设点 P 是△ABC 所在平面内一点，且BC →＋BA →＝2BP →，则 PC →＋PA →＝________. 0 [因为BC →＋BA →＝2BP →，由平行四边形法则知，点 P 为 AC 的中点，故PC →＋ PA →＝0.] 4．(教材改编)已知▱ABCD 的对角线 AC 和 BD 相交于点 O，且OA → ＝a，OB → ＝ b，则DC → ＝________，BC →＝________(用 a，b 表示)． b－a －a－b [如图，DC → ＝AB →＝OB → －OA → ＝b－a， BC →＝OC → －OB → ＝－OA → －OB → ＝－a－b.] 5．已知 a 与 b 是两个不共线向量，且向量 a＋λb 与－(b－3a)共线，则λ＝ ________. 【导学号：51062134】 －1 3 [由已知得 a＋λb＝－k(b－3a)， ∴ λ＝－k， 3k＝1， 得 λ＝－1 3 ， k＝1 3. ] 平面向量的有关概念 给出下列六个命题： ①若|a|＝|b|，则 a＝b 或 a＝－b； ②若AB →＝DC → ，则 ABCD 为平行四边形； ③若 a 与 b 同向，且|a|>|b|，则 a>b； ④λ，μ为实数，若λa＝μb，则 a 与 b 共线； ⑤λa＝0(λ为实数)，则λ必为零； ⑥a，b 为非零向量，a＝b 的充要条件是|a|＝|b|且 a∥b. 其中假命题的序号为________． ①②③④⑤⑥ [①不正确．|a|＝|b|.但 a，b 的方向不确定，故 a，b 不一定 是相等或相反向量； ②不正确．因为AB →＝DC → ，A，B，C，D 可能在同一直线上，所以 ABCD 不 一定是平行四边形． ③不正确．两向量不能比较大小． ④不正确．当λ＝μ＝0 时，a 与 b 可以为任意向量，满足λa＝μb，但 a 与 b 不一定共线． ⑤不正确．当λ＝1，a＝0 时，λa＝0. ⑥不正确．对于非零向量 a，b，a＝b 的充要条件是|a|＝|b|且 a，b 同向．] [规律方法] 1.(1)易忽视零向量这一特殊向量，误认为④是正确的；(2)充分 利用反例进行否定是对向量的有关概念题进行判定的行之有效的方法. 2．(1)相等向量具有传递性，非零向量平行也具有传递性．(2)共线向量(平 行向量)和相等向量均与向量的起点无关． 3．若 a 为非零向量，则 a |a| 是与 a 同向的单位向量，－ a |a| 是与 a 反向的单位 向量． [变式训练 1] 设 a0 为单位向量，①若 a 为平面内的某个向量，则 a＝|a|a0； ②若 a 与 a0 平行，则 a＝|a|a0；③若 a 与 a0 平行且|a|＝1，则 a＝a0.上述命题中， 假命题的个数是 ( ) A．0 B．1 C．2 D．3 D [向量是既有大小又有方向的量，a 与|a|a0 的模相同，但方向不一定相同， 故①是假命题；若 a 与 a0 平行，则 a 与 a0 的方向有两种情况：一是同向，二是 反向，反向时 a＝－|a|a0，故②③也是假命题．综上所述，假命题的个数是 3.] 平面向量的线性运算 (1)设 D，E，F 分别为△ABC 的三边 BC，CA，AB 的中点，则EB →＋FC → ＝( ) A.BC → B.1 2AD → C.AD → D.1 2BC → (2)(2017·杭州二中模拟)在梯形 ABCD 中，AD∥BC，已知 AD＝4，BC＝6， 若CD → ＝mBA →＋nBC → (m，n∈R)，则m n ＝( ) A．－3 B．－1 3 C.1 3 D．3 (1)C (2)A [(1)如图，EB →＋FC →＝EC →＋CB →＋FB →＋BC → ＝EC →＋FB →＝1 2(AC →＋AB → ) ＝1 2·2AD → ＝AD → . (2)如图，过 D 作 DE∥AB，CD → ＝mBA →＋nBC →＝CE →＋ED → ＝－1 3BC →＋BA →， 所以 n＝－1 3 ，m＝1，所以m n ＝－3.故选 A.] [规律方法] 向量的线性运算的求解方法 (1)进行向量运算时，要尽可能转化到平行四边形或三角形中，选用从同一 顶点出发的基本向量或首尾相接的向量，运用向量加、减法运算及数乘运算来求 解． (2)除了充分利用相等向量、相反向量和线段的比例关系外，有时还需要利 用三角形中位线、相似三角形对应边成比例等平面几何的性质，把未知向量转化 为与已知向量有直接关系的向量来求解． [变式训练 2] (1)设 M 为平行四边形 ABCD 对角线的交点，O 为平行四边 形 ABCD 所在平面内任意一点，则OA → ＋OB → ＋OC → ＋OD → 等于( ) A.OM → B．2OM → C．3OM → D．4OM → (2)已知 D 为三角形 ABC 边 BC 的中点，点 P 满足PA →＋BP →＋CP →＝0，AP →＝λPD → ， 则实数λ的值为________． (1)D (2)－2 [(1)因为 M 是 AC 和 BD 的中点，由平行四边形法则，得OA → ＋ OC → ＝2OM → ，OB → ＋OD → ＝2OM → ，所以OA → ＋OB → ＋OC → ＋OD → ＝4OM → .故选 D. (2)因为 D 是 BC 的中点，则AB →＋AC →＝2AD → . 由PA →＋BP →＋CP →＝0，得BA →＝PC → . 又AP →＝λPD → ， 所以点 P 是以 AB，AC 为邻边的平行四边形的第四个顶点，因此AP →＝AB →＋AC → ＝2AD → ＝－2PD → ，所以λ＝－2.] 共线向量定理的应用 设两个非零向量 a 与 b 不共线， (1)若AB →＝a＋b，BC →＝2a＋8b，CD → ＝3(a－b)，求证：A，B，D 三点共线； (2)试确定实数 k，使 ka＋b 和 a＋kb 共线. 【导学号：51062135】 [解] (1)证明：∵AB →＝a＋b，BC →＝2a＋8b，CD → ＝3(a－b)，2 分 ∴BD → ＝BC →＋CD → ＝2a＋8b＋3(a－b) ＝2a＋8b＋3a－3b＝5(a＋b)＝5AB → . ∴AB →，BD → 共线，又∵它们有公共点 B， ∴A，B，D 三点共线.6 分 (2)∵ka＋b 和 a＋kb 共线， ∴存在实数λ，使 ka＋b＝λ(a＋kb)， 即 ka＋b＝λa＋λkb，∴(k－λ)a＝(λk－1)b.10 分 ∵a，b 是两个不共线的非零向量， ∴k－λ＝λk－1＝0，∴k2－1＝0，∴k＝±1.14 分 [规律方法] 共线向量定理的应用 (1)证明向量共线：对于向量 a，b，若存在实数λ，使 a＝λb，则 a 与 b 共线． (2)证明三点共线：若存在实数λ，使AB →＝λAC →，则 A，B，C 三点共线． (3)求参数的值：利用共线向量定理及向量相等的条件列方程(组)求参数的 值． 易错警示：证明三点共线时，需说明共线的两向量有公共点． [变式训练 3] (1)已知向量AB →＝a＋3b，BC →＝5a＋3b，CD → ＝－3a＋3b，则 ( ) A．A，B，C 三点共线 B．A，B，D 三点共线 C．A，C，D 三点共线 D．B，C，D 三点共线 (2)设向量 a，b 不平行，向量λa＋b 与 a＋2b 平行，则实数λ＝________. (1)B (2)1 2 [(1)∵BD → ＝BC →＋CD → ＝2a＋6b＝2(a＋3b)＝2AB →， ∴BD → ，AB →共线，又有公共点 B， ∴A，B，D 三点共线．故选 B. (2)∵λa＋b 与 a＋2b 平行，∴λa＋b＝t(a＋2b)， 即λa＋b＝ta＋2tb，∴ λ＝t， 1＝2t， 解得 λ＝1 2 ， t＝1 2. ] [思想与方法] 1．向量加法的三角形法则应注意“首尾相接，指向终点”；向量减法的三 角形法则应注意“起点重合，指向被减向量”；平行四边形法则应注意“起点重 合”． 2．证明三点共线问题，可用向量共线来解决，但应注意向量共线与三点共 线的区别与联系，当两向量共线且有公共点时，才能得出三点共线． 3．对于三点共线有以下结论：对于平面上的任一点 O，OA → ，OB → 不共线，满 足OP → ＝xOA → ＋yOB → (x，y∈R)，则 P，A，B 共线⇔x＋y＝1. [易错与防范] 1．解决向量的概念问题要注意两点：一是向量的大小与方向；二是考虑零 向量是否也满足条件．要特别注意零向量的特殊性． 2．在利用向量减法时，易弄错两向量的顺序，从而求得所求向量的相反向 量，导致错误． 3．在向量共线的条件中易忽视“a≠0”，否则λ可能不存在，也可能有无数个． 课时分层训练(二十二) 平面向量的概念及线性运算 A 组 基础达标 (建议用时：30 分钟) 一、选择题 1．在△ABC 中，已知 M 是 BC 中点，设CB →＝a，CA →＝b，则AM → ＝( ) A.1 2a－b B.1 2a＋b C．a－1 2b D．a＋1 2b A [AM → ＝AC →＋CM → ＝－CA →＋1 2CB →＝－b＋1 2a，故选 A.] 2．已知AB →＝a＋2b，BC →＝－5a＋6b，CD → ＝7a－2b，则下列一定共线的三点 是( ) A．A，B，C B．A，B，D C．B，C，D D．A，C，D B [因为AD → ＝AB →＋BC →＋CD → ＝3a＋6b＝3(a＋2b)＝3AB →，又AB →，AD → 有公共 点 A， 所以 A，B，D 三点共线．] 3．在△ABC 中，已知 D 是 AB 边上的一点，若AD → ＝2DB → ，CD → ＝1 3CA →＋λCB →， 则λ等于( ) A.2 3 B.1 3 C．－1 3 D．－2 3 A [∵AD → ＝2DB → ，即CD → －CA →＝2(CB →－CD → )， ∴CD → ＝1 3CA →＋2 3CB →，∴λ＝2 3.] 4．设 a，b 都是非零向量，下列四个条件中，使 a |a| ＝ b |b| 成立的充分条件是 ( ) 【导学号：51062136】 A．a＝－b B．a∥b C．a＝2b D．a∥b 且|a|＝|b| C [ a |a| ＝ b |b| ⇔a＝|a|b |b| ⇔a 与 b 共线且同向⇔a＝λb 且λ>0.B，D 选项中 a 和 b 可能反向．A 选项中λ<0，不符合λ>0.] 5．设 D，E，F 分别是△ABC 的三边 BC，CA，AB 上的点，且DC → ＝2BD → ，CE → ＝2EA →，AF →＝2FB →，则AD → ＋BE →＋CF →与BC → ( ) A．反向平行 B．同向平行 C．互相垂直 D．既不平行也不垂直 A [由题意得AD → ＝AB →＋BD → ＝AB →＋1 3BC →， BE →＝BA →＋AE →＝BA →＋1 3AC →， CF →＝CB →＋BF →＝CB →＋1 3BA →， 因此AD → ＋BE →＋CF →＝CB →＋1 3(BC →＋AC →－AB → ) ＝CB →＋2 3BC →＝－1 3BC →， 故AD → ＋BE →＋CF →与BC →反向平行．] 二、填空题 6．已知 O 为四边形 ABCD 所在平面内一点，且向量OA → ，OB → ，OC → ，OD → 满足 等式OA → ＋OC → ＝OB → ＋OD → ，则四边形 ABCD 的形状为________. 【导学号：51062137】 平行四边形 [由OA → ＋OC → ＝OB → ＋OD → 得OA → －OB → ＝OD → －OC → ， 所以BA →＝CD → ，所以四边形 ABCD 为平行四边形．] 7．在矩形 ABCD 中，O 是对角线的交点，若BC → ＝5e1，DC → ＝3e2，则OC → ＝ ________.(用 e1，e2 表示) 5 2e1＋3 2e2 [在矩形 ABCD 中，因为 O 是对角线的交点，所以OC → ＝1 2AC →＝1 2(AB → ＋AD → )＝1 2(DC → ＋BC → )＝1 2(5e1＋3e2)．] 8．在△ABC 中，点 M，N 满足AM → ＝2MC → ，BN →＝NC → .若MN → ＝xAB →＋yAC →，则 x＝________；y＝________. 1 2 －1 6 [∵AM → ＝2MC → ，∴AM → ＝2 3AC → . ∵BN →＝NC → ，∴AN →＝1 2(AB →＋AC → )， ∴MN＝AN →－AM → ＝1 2(AB →＋AC → )－2 3AC → ＝1 2AB →－1 6AC → . 又MN → ＝xAB →＋yAC →，∴x＝1 2 ，y＝－1 6.] 三、解答题 9．在△ABC 中，D，E 分别为 BC，AC 边上的中点，G 为 BE 上一点，且 GB＝2GE，设AB →＝a，AC →＝b，试用 a，b 表示AD → ，AG → . 【导学号：51062138】 图 411 [解] AD → ＝1 2(AB →＋AC → )＝1 2a＋1 2b.4 分 AG → ＝AB →＋BG → ＝AB →＋2 3BE →＝AB →＋1 3(BA →＋BC → ) ＝2 3AB →＋1 3(AC →－AB → ) ＝1 3AB →＋1 3AC → ＝1 3a＋1 3b.14 分 10．设两个非零向量 e1 和 e2 不共线． (1)如果AB →＝e1－e2，BC →＝3e1＋2e2，CD → ＝－8e1－2e2， 求证：A，C，D 三点共线； (2)如果AB →＝e1＋e2，BC →＝2e1－3e2，CD → ＝2e1－ke2，且 A，C，D 三点共线， 求 k 的值． [解] (1)证明：∵AB →＝e1－e2，BC →＝3e1＋2e2， CD → ＝－8e1－2e2， ∴AC →＝AB →＋BC →＝4e1＋e2 ＝－1 2(－8e1－2e2)＝－1 2CD → ， ∴AC →与CD → 共线.4 分 又∵AC →与CD → 有公共点 C，∴A，C，D 三点共线.7 分 (2)AC →＝AB →＋BC →＝(e1＋e2)＋(2e1－3e2)＝3e1－2e2.9 分 ∵A，C，D 三点共线， ∴AC →与CD → 共线，从而存在实数λ使得AC →＝λCD → ，12 分 即 3e1－2e2＝λ(2e1－ke2)， 得 3＝2λ， －2＝－λk， 解得 λ＝3 2 ， k＝4 3. 15 分 B 组 能力提升 (建议用时：15 分钟) 1．设 M 是△ABC 所在平面上的一点，且MB → ＋3 2MA → ＋3 2MC → ＝0，D 是 AC 的 中点，则|MD → | |BM → | 的值为 ( ) A.1 3 B.1 2 C．1 D．2 A [∵D 是 AC 的中点，延长 MD 至 E，使得 DE＝MD(图略)，∴四边形 MAEC 为平行四边形，∴MD → ＝1 2ME → ＝1 2(MA → ＋MC → )．∵MB → ＋3 2MA → ＋3 2MC → ＝0，∴MB → ＝－3 2(MA → ＋MC → )＝－3MD → ，∴|MD → | |BM → | ＝ |MD → | |－3MD → | ＝1 3 ，故选 A.] 2．(2017·浙江嘉兴高三双基测试)如图 412，在△ABC 中，AB＝2，BC＝3， ∠ABC＝60°，AH⊥BC 于点 H，M 为 AH 的中点．若AM → ＝λAB →＋μBC →，则λ＋μ＝ ________. 【导学号：51062139】 图 412 2 3 [因为 AB＝2，∠ABC＝60°，AH⊥BC，所以 BH＝1. 因为点 M 为 AH 的中点，所以AM → ＝1 2AH → ＝1 2(AB →＋BH → )＝1 2 AB →＋1 3BC → ＝1 2AB →＋ 1 6BC →，又AM → ＝λAB →＋μBC →，所以λ＝1 2 ，μ＝1 6 ，所以λ＋μ＝2 3.] 3．已知 a，b 不共线，OA → ＝a，OB → ＝b，OC → ＝c，OD → ＝d，OE → ＝e，设 t∈R， 如果 3a＝c,2b＝d，e＝t(a＋b)，是否存在实数 t 使 C，D，E 三点在一条直线上？ 若存在，求出实数 t 的值，若不存在，请说明理由． [解] 由题设知，CD → ＝d－c＝2b－3a，CE → ＝e－c＝(t－3)a＋tb，C，D，E 三点在一条直线上的充要条件是存在实数 k，使得CE →＝kCD → ，即(t－3)a＋tb＝－ 3ka＋2kb，3 分 整理得(t－3＋3k)a＝(2k－t)b.7 分 因为 a，b 不共线，所以有 t－3＋3k＝0， t－2k＝0， 13 分 解之得 t＝6 5.故存在实数 t＝6 5 使 C，D，E 三点在一条直线上.15 分