- 2021-06-15 发布 |
- 37.5 KB |
- 14页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学选修2-3公开课课件2_4正态分布(2)
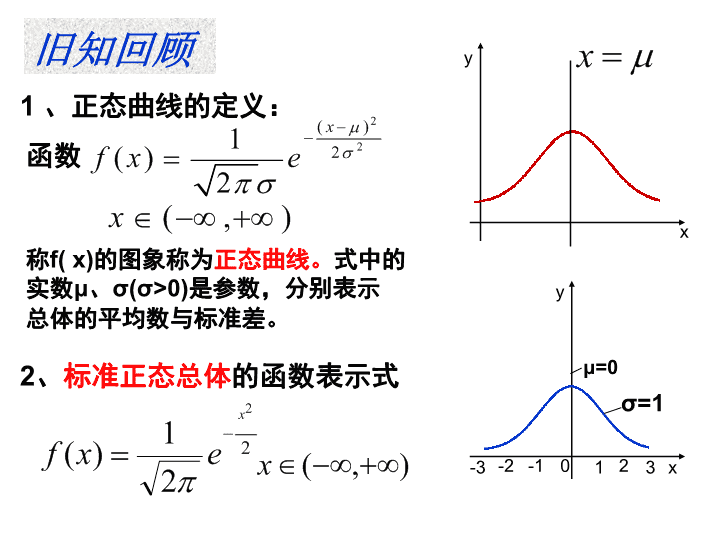
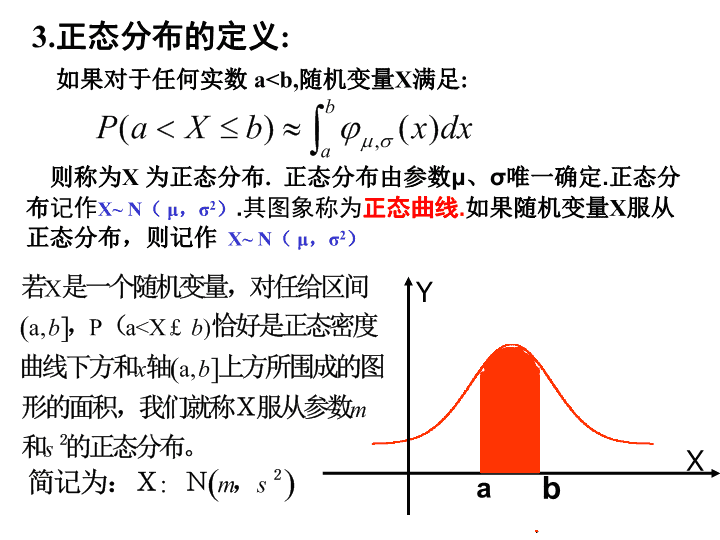
2.4 正态分布 ( 二 ) 高二数学 选修 2-3 旧知回顾 函数 称 f( x) 的图象称为 正态曲线。 式中的 实数 μ 、 σ(σ>0) 是参数,分别表示 总体的平均数与标准差。 1 、正态曲线的定义: x y 2 、 标准正态总体 的函数表示式 0 1 2 -1 -2 x y -3 3 μ=0 σ=1 3. 正态分布的定义 : 如果对于任何实数 a查看更多
相关文章
- 当前文档收益归属上传用户