高中数学北师大版新教材必修一同步课件:阶段提升课 第一课 集合与常用逻辑用语
阶段提升课
第一课 集合与常用逻辑用语
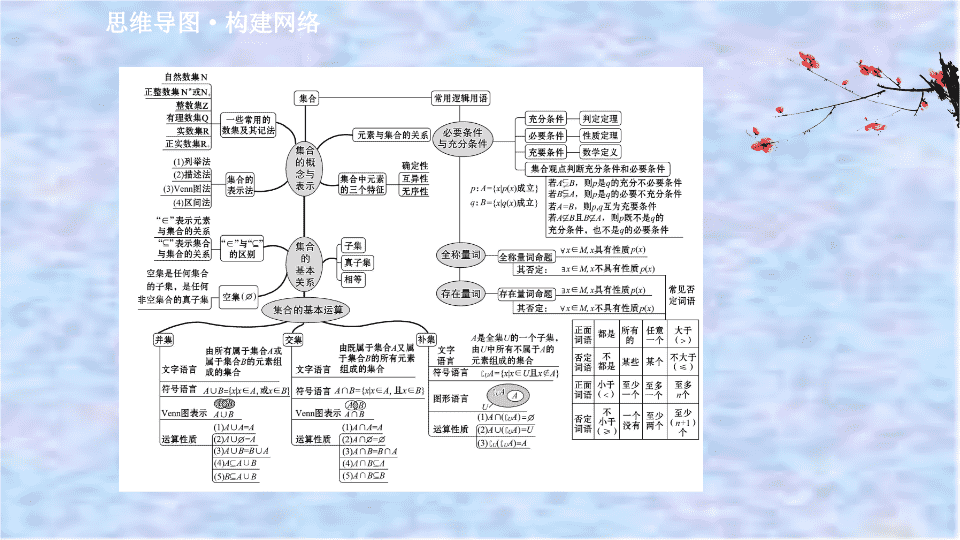
思维导图
·
构建网络
考点整合
·
素养提升
题组训练一 元素与集合、集合与集合的关系
1.(2020·
南京高一检测
)
若
4∈{
x+2,x
2
}
,则实数
x
的值为
(
)
A.-2 B.2 C.2
或
-2 D.2
或
4
【
解析
】
选
A.
因为
4∈
{
x+2,x
2
}
,
所以
解得
x=-2.
2.(2020·
青岛高一检测
)
已知集合
A={x|2a-3
0
得
x>2,
则集合
B={x|x>2},
所以
∁
R
B={x|x≤2},
又集合
A={x|1a+3,
解得
a>3;
当
A≠∅
时
,
若
A∩B=∅,
如图所示
,
则 解得
- ≤a≤2,
综上
,a
的取值范围是
- ≤a≤2
或
a>3.
【
方法技巧
】
1.
集合基本运算的方法
(1)
定义法或
Venn
图法
:
集合是用列举法给出的
,
运算时可直接借助定义求解
,
或把元素在
Venn
图中表示出来
,
借助
Venn
图观察求解
.
(2)
数轴法
:
集合是用不等式
(
组
)
给出的
,
运算时可先将不等式在数轴中表示出来
,
然后借助数轴求解
.
2.
集合与不等式结合的运算包含的类型及解决办法
(1)
不含字母参数
:
直接将集合中的不等式解出
,
在数轴上求解
.
(2)
含有字母参数
:
若字母的取值影响到不等式的解
,
要先对字母分类讨论
,
再求解不等式
,
然后在数轴上求解
.
题组训练三 充分条件和必要条件
1.|m|≠2
是
m≠2
的
条件
(
)
A.
充要
B.
充分不必要
C.
必要不充分
D.
既不充分也不必要
【
解析
】
选
B.|m|≠2
⇒
m≠±2,
而由
m≠2,
推不出
|m|≠2.
所以
|m|≠2
是
m≠2
的充分不必要条件
.
2.(2020·
大连高一检测
)
已知
p:4x-m<0,q:1≤3-x≤4,
若
p
是
q
的一个必要不充
分条件
,
则实数
m
的取值范围为
(
)
A.{m|m≥8} B.{m|m
>
8}
C.{m|m
>
-4} D.{m|m≥-4}
【
解析
】
选
B.
设
A={
x|4x-m
<
0
}
,则
A= ,
设
B={
x|1≤3-x≤4
}
,
则
B= ,
因为
p
是
q
的一个必要不充分条件
,
所以
B A,
所以
>2,
即
m>8.
【
方法技巧
】
充分条件与必要条件的判断方法
(1)
定义法
(2)
集合法
:
写出集合
A={x|p(x)}
及
B={x|q(x)},
利用集合之间的包含关系加以判断
.
用集合法判断时
,
要尽可能用图示、数轴等几何方法
,
图形形象、直观
,
能简化解题过程
,
降低思维难度
.
题组训练四 全称量词命题和存在量词命题及其否定
1.
已知命题
p:∀n∈N
*
,n
2
> n-1,
则命题
p
的否定为
(
)
A.∀n∈N
*
,n
2
≤ n-1
B.∀n∈N
*
,n
2
<
n-1
C.∃n∈N
*
,n
2
≤
n-1
D.∃n∈N
*
,n
2
<
n-1
【
解析
】
选
C.“
∀
n∈N
*
,n
2
>
n-1
”
的否定是
“
∃
n∈N
*
,n
2
≤
n-1
”
.
2.
命题“存在实数
x∈M,
使得
x,3,4
能成为三角形的三边长”是假命题
,
则
x
的取值构成的集合
M=
.
【
解析
】
当命题“存在实数
x∈M,
使得
x,3,4
能成为三角形的三边长”是真命题时
,
可得
4-32,
所以
B=(2,+∞).
(2)
因为
A={
x|3a
<
x
<
a+2
}
为非空集合
,
所以
a+2>3a,
所以
a<1,
若
x∈A
是
x∈B
的充分不必要条件
,
则
A
B,
所以
3a≥2,
解得
a≥ ,
所以实数
a
的取值范围是
【
方法技巧
】
含有一个量词的命题的否定的方法
(1)
一般地
,
写含有一个量词的命题的否定
,
首先要明确这个命题是全称量词命题还是存在量词命题
,
并找到量词及相应结论
,
然后把命题中的全称量词改成存在量词
,
存在量词改成全称量词
,
同时否定结论
.
(2)
对于省略量词的命题
,
应先挖掘命题中隐含的量词
,
改写成含量词的完整形式
,
再依据规则来写出命题的否定
.