四省八校2020届高三上学期第一次教学质量检测考试 数学（理）

四省八校2020届高三上学期第一次教学质量检测考试 数学（理）

‎“四省八校”2020届高三第一次教学质量检测考试 数 学(理科)‎ ‎2019.10‎ 注意事项：‎ ‎1.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。‎ ‎2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。‎ ‎3.考试结束后，将本试卷和答题卡一并交回。‎ 一、选择题：本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一个选项是符合题目要求的。‎ ‎1.已知集合U＝{x∈N|－1≤x≤3}，A＝{1，3，5}，B＝{x|x2－2x－3＝0}，则(A∩B)＝‎ A.{1，2} B.{0，1，2} C.{3} D.{－1，0，1，2}‎ ‎2.已知命题p：，则 A. B.‎ C. D.‎ ‎3.若1ogab< logac，则下列不等式一定成立的是 A.abca ‎4.在△ABC中，，F为AD中点，则 A. B. C. D. ‎ ‎5.已知直线l的倾斜角α满足方程，则直线l的斜率为 A.－ B. C. 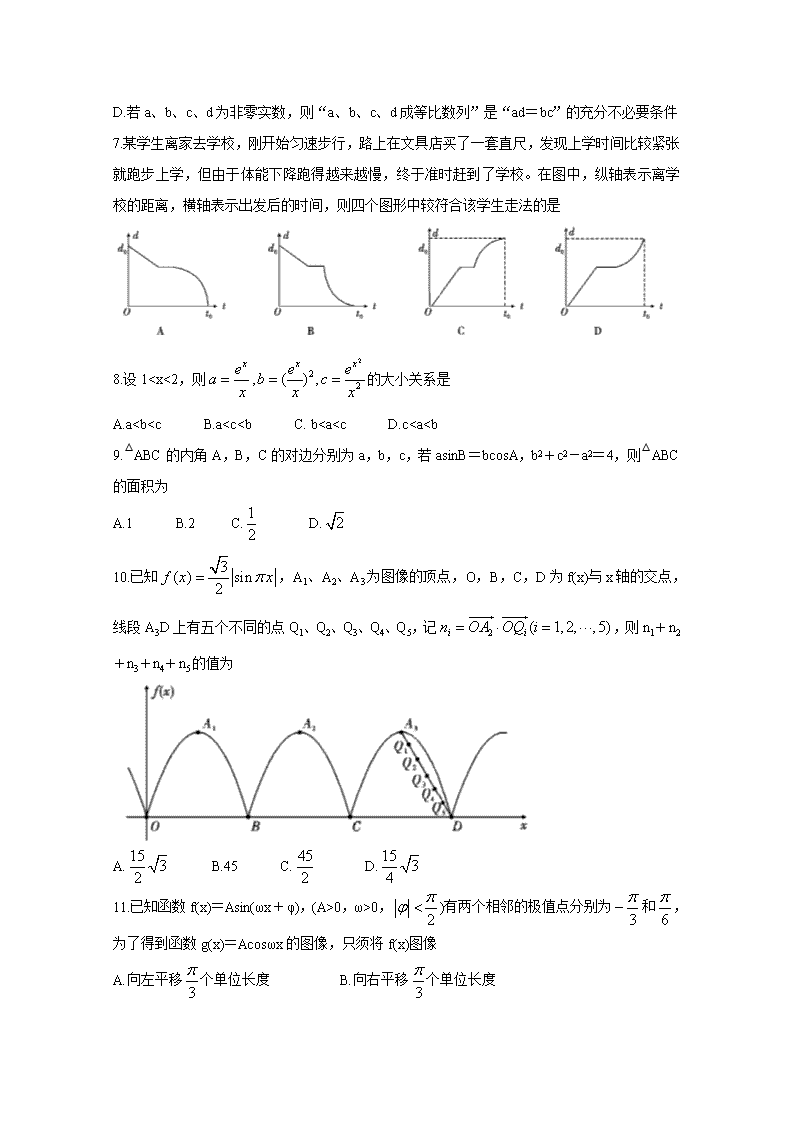D.－‎ ‎6.下列说法错误的是 A.已知04是与的夹角为锐角的充要条件 D.若a、b、c、d为非零实数，则“a、b、c、d成等比数列”是“ad＝bc”的充分不必要条件 ‎7.某学生离家去学校，刚开始匀速步行，路上在文具店买了一套直尺，发现上学时间比较紧张就跑步上学，但由于体能下降跑得越来越慢，终于准时赶到了学校。在图中，纵轴表示离学校的距离，横轴表示出发后的时间，则四个图形中较符合该学生走法的是 ‎8.设10，ω>0，)有两个相邻的极值点分别为和，为了得到函数g(x)＝Acosωx的图像，只须将f(x)图像 A.向左平移个单位长度 B.向右平移个单位长度 C.向左平移个单位长度 D.向右平移个单位长度 ‎12.已知f(x)＝(2x－1)ex－kx，若有且仅有两个整数值使得f(x)<0成立，则实数k的取值范围是 A.(e，] B.[，] C.[，] D.[，)∪(e，]‎ 二、填空题：本题共4小题，每小题5分，共20分。‎ ‎13.已知＝(m，2)，＝(，－3)，且//，则(－2)·＝ 。‎ ‎14.已知f(x)＝2sinx＋cosx，若α满足f(α)＋f’(α)＝，则tan α＝ 。‎ ‎15.已知数列{an}满足且a6＝6，则a2019＝ 。‎ ‎16.已知函数f(x)＝(x－2)ex＋e＋l，，对任意的，总存在使得g(x)≥f(x)成立，则a的范围为 。‎ 三、解答题：共70分。解答应写出文字说明、证明过程和演算步骤。‎ ‎17.(12分)‎ ‎△ABC的内角A，B，C所对的边分别为a，b，c，已知。‎ ‎(1)证明：B＝C；‎ ‎(2)若，△ABC的面积为，求a的值。‎ ‎18.(12分)‎ 数列{an}的前n项和记为Sn，a1 ＝9，an＋1＝2Sn ＋9，n∈N*，b1＝1，bn＋1－bn＝log3an。‎ ‎(1)求{an}的通项公式；‎ ‎(2)求证：对n∈N*，总有。‎ ‎19.(12分)‎ 已知函数。‎ ‎(1)求函数f(x)的单增区间；‎ ‎(Z)将y＝f(x)图象上的所有点向左平移θ(θ>0)个单位长度，所得图象关于直线对称，求θ的最小值。‎ ‎20.(12分)‎ 已知函数，f’(x)为f(x)的导数，证明：‎ ‎(1)f’(x)在区间(0，π)上有唯一零点；‎ ‎(2)f(x)有且仅有两个零点。‎ ‎21.(12分)‎ 已知函数f(x)＝x2－alnx有两个零点x1，x2(x14x0。‎ 请考生在第22、23两题中任选一题作答，如果多做，则按所做的第一题记分。作答时用铅笔在答题卡上把所选题目的题号涂黑。‎ ‎22.(10分)选修4－4：坐标系与参数方程 右图是某数学爱好者在平面直角坐标系下绘制的“心型曲线”，如果以坐标原点为极点，x轴正半轴为极轴建立极坐标系，则该“心型曲线”的极坐标方程是。‎ ‎(1)求该“心型曲线”的直角坐标方程；‎ ‎(2)已知P(2，0)，直线l：与“心型曲线”在y轴右侧交于A，B两点，求|PA|＋|PB|的值。‎ ‎23.(10分)选修4－5：不等式选讲 已知函数f(x)＝|x－1|＋|2x＋1|。‎ ‎(1)解关于x的不等式f(x)≤6；‎ ‎(2)记f(x)＝6的解集中的最大元素为n，若a，b，c均为正数，ab＋cb＋ac＝n。证明：a＋b＋c≥。‎