2018人教A版数学必修二 4

2018人教A版数学必修二 4

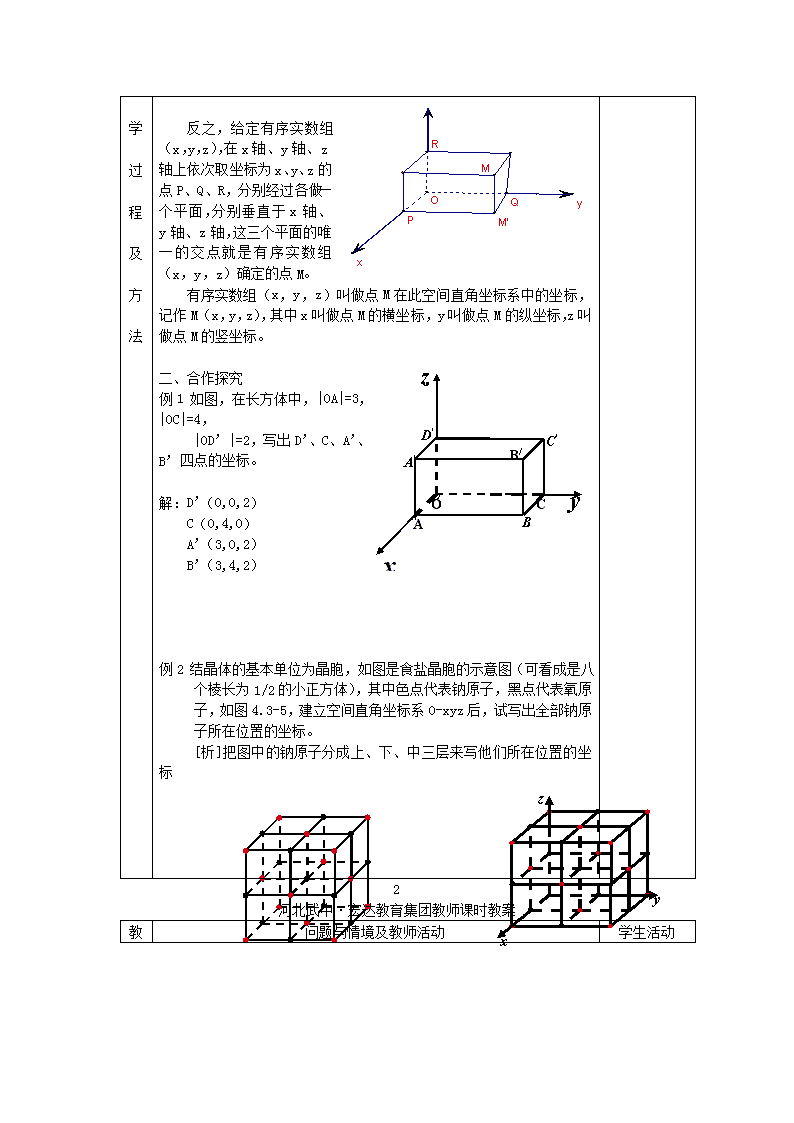
备课人 授课时间 课题 ‎4.3.1‎空间直角坐标系 ‎4.3.2‎空间两点间的距离公式 课标要求 在空间直角坐标系下，两点间的距离公式的推导，会求空间两点间的距离 教 学 目 标 知识目标 1、 感受空间直角坐标系建立的背景 ‎2、掌握两点间的距离公式的推导，会求空间两点间的距离。‎ 技能目标 掌握在空间直角坐标系下，两点间的距离公式的推导，会求空间两点间的距离 情感态度价值观 类比思想的运用 重点 ‎1、空间直角坐标系中点的表示；2、空间直角坐标下两点间距离公式及其应用。‎ 难点 两点间距离公式的推导。‎ 教 学 过 程 及 方 法 问题与情境及教师活动 学生活动 ‎ ‎ ‎ 一、空间直角坐标系 ‎1、空间直角坐标系的建立：‎ 如右图，OABC-D’A’B’C’为单位正方体，以_________为原点，以___________________为单位正方向，以______________为单位长，建立三条数轴______________,这样就建立了空间直角坐标系_______，其中O为________，x轴、y轴、z轴为_______，__________为坐标平面，分别为__________。‎ ‎ 2、右手直角坐标系 本书中建立的空间直角坐标系均为___________，右手拇指指向________，食指指向 ________，中指指向____________‎ ‎ 3、空间直角坐标系中任意一点M的坐标表示 如下图，设点M为空间一定点，过点M分别做垂直于x轴、y轴、z轴的平面依次交x轴、y轴、z轴于P、Q、R，设P、Q、R在x轴、y轴、z轴的坐标分别为x、y、z，则的坐标为（x，y，z）。‎ ‎1‎ 河北武中·宏达教育集团教师课时教案 点评：由多个平面图形围成的几何体，它们的侧面展开图还是平面图形，计算它们的表面积就是计算它的各个侧面面积和底面面积之和．‎ 教 问题与情境及教师活动 学生活动 学 过 程 及 方 法 反之，给定有序实数组（x，y，z），在x轴、y轴、z轴上依次取坐标为x、y、z的点P、Q、R，分别经过各做一个平面，分别垂直于x轴、y轴、z轴，这三个平面的唯一的交点就是有序实数组（x，y，z）确定的点M。‎ 有序实数组（x，y，z）叫做点M在此空间直角坐标系中的坐标，记作M（x，y，z），其中x叫做点M的横坐标，y叫做点M的纵坐标，z叫做点M的竖坐标。‎ B A x B/‎ C O 二、合作探究 例1 如图，在长方体中，|OA|=3，|OC|=4，‎ ‎|OD’|=2，写出D’、C、A’、B’四点的坐标。‎ 解：D’（0,0,2）‎ ‎ C（0,4,0）‎ ‎ A’（3,0,2）‎ ‎ B’（3,4,2） ‎ 例2 结晶体的基本单位为晶胞，如图是食盐晶胞的示意图（可看成是八个棱长为1/2的小正方体），其中色点代表钠原子，黑点代表氧原子，如图4.3-5，建立空间直角坐标系O-xyz后，试写出全部钠原子所在位置的坐标。‎ ‎[析]把图中的钠原子分成上、下、中三层来写他们所在位置的坐标 ‎2‎ 河北武中·宏达教育集团教师课时教案 教 问题与情境及教师活动 学生活动 学 过 程 及 方 法 三、空间两点间的距离公式 ‎1、求空间中两点间距离的引入 距离是几何中的基本度量，几何问题和一些实际问题经常涉及距离，如建筑设计中常常需要计算空间两点间的距离，你能用两点的坐标表示这两点间的距离吗？‎ ‎2、空间中两点间距离公式的推导 ‎（1）先求点P（x，y，z）到坐标原点的距离。‎ ‎　 如图，设点P在xOy平面上的射影是B（PB垂直平面xOy），点B坐标为（x，y，0）。‎ ‎∣OB∣＝，‎ ‎∣OP∣＝，‎ 由∣PB∣＝z，得：‎ ‎∣OP∣＝，‎ 这说明，在空间直角坐标系Oxyz中，任意一点P（x，y，z）到坐标原点的距离 ‎∣OP∣＝‎ ‎（2）求空间任意两点间的距离 设点P1（x1，y1，z1），P2（x2，y2，z2）是空间中任意两点，且点P1，P2在xOy平面的射影分别为M，N，那么M，N坐标为M（x1，y1，0），N（x2，y2，0），‎ 在xOy平面上，‎ ‎∣MN∣＝‎ 过点P1作P2N的垂线，垂足为H，则 ‎∣MP1∣＝∣z1∣，∣NP2∣＝∣z2∣‎ 所以，∣HP2∣＝∣z1－z2∣，‎ ‎∣HP1∣＝∣MN∣＝‎ 根据勾股定理，得 ‎∣P1P2∣＝‎ ‎＝‎ ‎3‎ 河北武中·宏达教育集团教师课时教案 教 问题与情境及教师活动 学生活动 学 过 程 及 方 法 因此，空间中两点P1（x1，y1，z1），P2（x2，y2，z2）之间的距离为：‎ ‎∣P1P2∣＝＝‎ 类比平面两点间的距离公式，有什么不同？有何相似之处？通过对比已经熟悉的公式来记忆新的公式，能加深印象。‎ ‎3、练习 P138　第1、2题 四、小结：‎ ‎1、空间直角坐标系中点的表示 ‎2、在空间直角坐标系下，两点间的距离公式的推导，并对比平面上两点间距离公式，学会类比思想，会求空间两点间的距离。‎ 教 学 小 结 课后 反思 ‎ ‎ ‎4‎