第三章 函数

第三章 函数

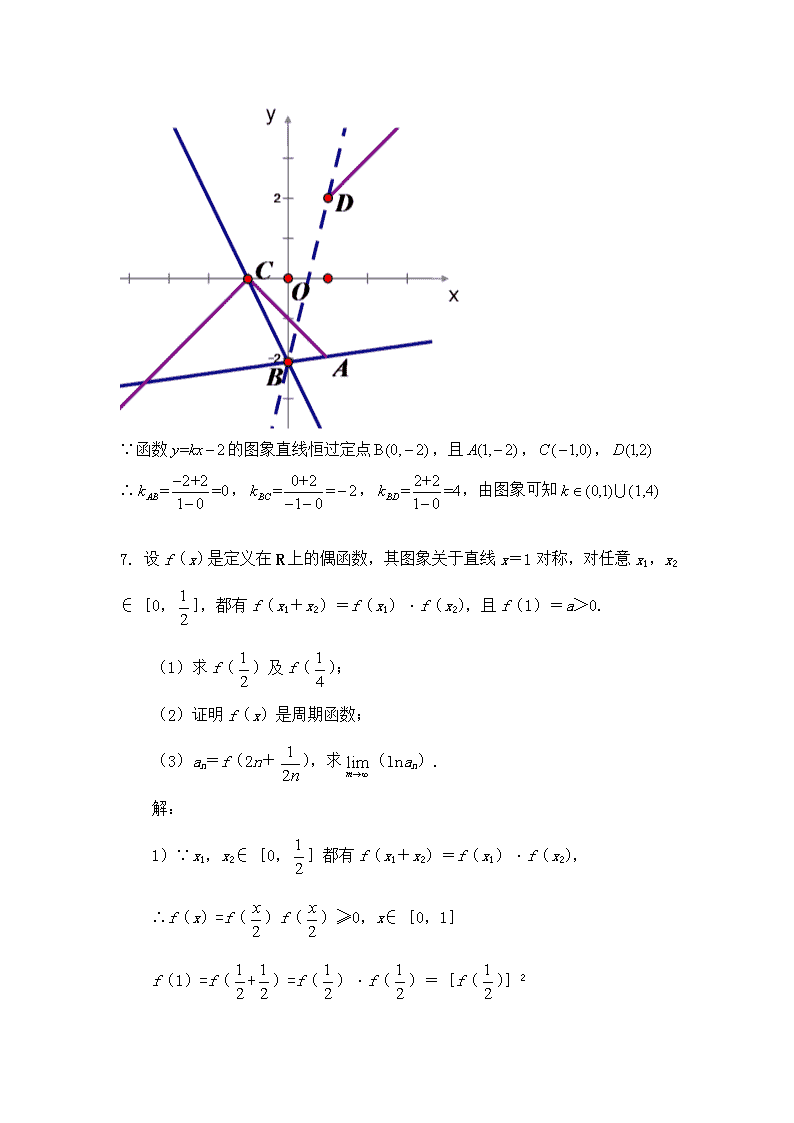
第三章 函数 ‎1. 已知函数，求的值. ‎ 解：由 ‎ ‎ ‎ ‎ ‎ ‎2．已知函数 求的表达式.‎ 解：设 ‎ 解得 ‎ ‎∴ ‎ 即 ‎ ‎3．已知函数，若存在，使，求实数的取值范围.‎ 解： ‎ ‎ ‎ ‎ 或 ‎ 1. 函数y=xcosx + sinx 的图象大致为 （ ） ‎ 解析：函数y=xcosx + sinx为奇函数，所以图象关于原点对称，所以排除B，C.当时，,排除A,选D.‎ ‎5.函数的图象大致是（ ）‎ 解析：首先考虑当x<0时,函数值应为正值,所以排除选项B,当x=0时解析式没有意义,故排除选项A,当x无穷大时,考虑指数函数比幂函数增长快,所以函数值越来越小,故选C.‎ ‎6.已知函数的图象与函数的图象恰有两个交点，则实数k的取值范围是 .‎ 解析：根据绝对值的意义，在直角坐标系中作出该函数的图象如图所示：‎ ‎∵函数的图象直线恒过定点，且，，‎ ‎∴，，，由图象可知 ‎7. 设f（x）是定义在R上的偶函数，其图象关于直线x＝1对称，对任意x1，x2∈［0，］，都有f（x1＋x2）＝f（x1）·f（x2），且f（1）＝a＞0.‎ ‎（1）求f（）及f（）；‎ ‎（2）证明f（x）是周期函数；‎ ‎（3）an＝f（2n＋），求（lnan）.‎ 解：‎ ‎1）∵x1，x2∈［0，］都有f（x1＋x2）＝f（x1）·f（x2），‎ ‎∴f（x）=f（）f（）≥0，x∈［0，1］‎ f（1）=f（+）=f（）·f（）＝［f（）］2‎ f（）=f（+）=f（）·f（）=[f（）]2，f（1）=a＞0，‎ ‎∴．‎ ‎（2）同上题（2）‎ ‎（3）∵x∈［0，］满足f（x1＋x2）＝f（x1）f（x2），I＝2n（n∈Z）‎ ‎∴f（x1＋2n+x2＋2n）＝f（x1＋2n）·f（x2＋2n），‎ ‎∵x1，x2在［2n，＋2n］中也满足f（x1＋x2）＝f（x1）·f（x2）‎ 又∵f（1）=f（1）·f（0），∴f（0）=1，∴f（2n）=1‎ 又∵f（）＝f2（），又∵f（）＝a，∴f（）＝a ‎∴an＝f（2n）f（）＝a，∴‎ ‎8.已知函数f（x）=ax+（a＞1）.‎ ‎（1）证明：函数f（x）在（－1，+∞）上为增函数；‎ ‎（2）用反证法证明方程f（x）=0没有负数根.‎ 证明：（1）设－1＜x1＜x2‎ 因为x2－x1＞0，又a＞1，所以＞1，而－1＜x1＜x2，所以x1+1＞0，x2+1＞0，所以f（x2）－f（x1）＞0，∴f（x）在（－1，+∞）上为增函数 ‎（2）设x0为方程f（x）=0的负根，则有.‎ 即 显然x0≠－1‎ 当0＞x0＞－1时，1＞x0+1＞0，＞3，－1+＞2‎ 而＜＜1，这是不可能的，即不存在0＞x0＞－1的解 x0＜－1时，x0+1＜0，‎ 而＞0，矛盾，即不存在x0＜－1的解.‎ 综上，即不存在负根.‎ ‎9.设f（x）是定义在R上的偶函数，其图象关于直线x＝1对称，对任意x1，x2∈［0，］，都有f（x1＋x2）＝f（x1）·f（x2）.‎ ‎（1）设f（1）＝2，求f（），f（）；‎ ‎（2）证明f（x）是周期函数；‎ ‎（1）解：由f（x1＋x2）＝f（x1）·f（x2），x1，x2∈［0，］知 f（x）=f（）·f（）≥0，x∈［0，1］，∵f（1）=f（+）=f（）·f（）=[f（）]2，f（1）＝2，∴f（）＝2．‎ ‎∵f（）=f（+）=f（）·f（）=[f（）]2，f（）=2，‎ ‎∴f（）=2．‎ ‎（2）证明：依题设y=f（x）关于直线x=1对称，‎ ‎∴f（x）=（1+1－x），f（x）=f（2－x）‎ 又∵f（－x）=f（x），∴f（－x）=f（2－x），∴f（x）=f（2+x），‎ ‎∴f（x）是R上的周期函数，且2是它的一个周期．‎ ‎10. 已知抛物线经过点．‎ ‎（1）求抛物线的解析式．‎ ‎（2）设抛物线顶点为，与轴交点为．求的值．‎ ‎（3）设抛物线与轴的另一个交点为，求四边形的面积．‎ ‎ ‎ ‎ ‎ 解：（1）解方程组 得，． ‎ ‎（2）顶点． ‎ ‎（3）在中，令得，，‎ 令得或，． ‎ 四边形（面积单位）‎ ‎11．已知函数y=和y=kx+l(k≠O)．‎ ‎ (1)若这两个函数的图象都经过点(1，a)，求a和k的值；‎ ‎ (2)当k取何值时，这两个函数的图象总有公共点?‎ 解；(1) ∵两函数的图象都经过点(1，a)，∴∴‎ ‎ (2)将y＝代人y=kx+l，消去y．得kx2+x一2=0．‎ ‎ ∵k≠O，∴要使得两函数的图象总有公共点，只要△≥0即可．‎ ‎ ∵△＝1＋8k，‎ ‎ ∴1+8k≥0，解得k≥一 ‎ ∴k≥一且k≠0．‎ ‎12．如图9，抛物线y=ax2+8ax+12a与轴交于A、B两点（点A在点B的左侧），抛物线上另有一点在第一象限，满足∠ ACB为直角,且恰使△OCA∽△OBC.‎ ‎(1) 求线段OC的长. ‎ ‎(2) 求该抛物线的函数关系式．‎ ‎(3) 在轴上是否存在点P，使△BCP为等腰三角形？‎ 若存在，求出所有符合条件的P点的坐标；若不存在，‎ 请说明理由.‎ ‎ ‎ 解：（1）；（2）；（3）4个点：‎ 13. 已知函数f(x)=|-4x+3|‎ (1) 求函数f(x)的单调区间，并指出其增减性；‎ (2) 求集合M={m|使方程f(x)=mx有四个不相等的实根}.‎ 解：当-4x+3≥0，即x≤1或x≥3时，‎ f(x)=-4x+3=-1; ‎ 当-4x+3<0，即1-1,且当x[-,)时，f(x)≤g(x),求a的取值范围.‎ 解：(1)当a=－2时，不等式f(x)1‎ 其图像如图所示，从图象可知，当且仅当x(0,2)时，y<0‎ 所以原不等式的解集为{x|0

查看更多