浅水域生存工况下系泊浮筒系统三维运动

浅水域生存工况下系泊浮筒系统三维运动

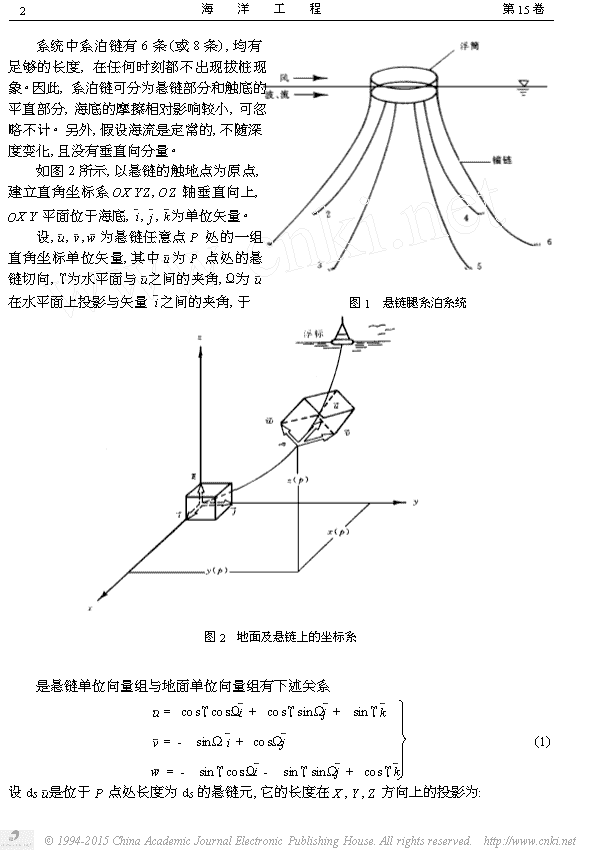
浅水域生存工况下系泊浮筒系统三维运动3张挺孙明光(中山大学,广州510275)摘要本文提出一个浅水域生存工况下,多锚链系泊浮筒系统三维运动的工程计算模型,对链系采用射的法计算,使其与浮筒运动计算相匹配。对不同的风波流方向及链刚度,计算了浮筒的运动及链力,结果显示本文的模型是合理的。关键词生存工况浅水域浮筒链系三维运动前言1悬链腿单点系泊系统,由于其适应性广,技术成熟,安装容易,对水深和油轮大小不是非常敏感,因而在世界上被大量使用。在我国,也开始使用这类系统。在一般情况下,认为系统处于作业工况(即有油轮系泊)时,其系泊链张力最大。这方面已有不少的工作。但是,我们对一些系统的初步估算说明,在浅水情形,系统处于生存工况下,虽然油轮撒离了,但浮筒却有更激烈的运动,从而导致系泊链会发生更大的张力。实践证实了这种情况存在的可能性。目前,有关这方面的问题,研究结果很少。文献1仅研究多锚链系泊浮筒的纵荡运动,文献2则考虑了纵荡与升沉的非耦合运动,文献3虽考虑了纵荡、升沉及纵摇的耦合运动,但属于弱非线性问题,不适合浅水及生存工况的计算,另外,它难以推广到三维运动情形,文献4研究了船舶在波中大振幅运动问题,计算时湿表面采用瞬时值,文献5研究了波流共存情形下的CD及CM值计算方法,文献6用时域模拟了二阶波与系泊柱之间的相互作用,文献7研究了物体靠近海底时,CD、CM值的变化。我们注意到浮筒系泊系统,在浅水生存工况条件下,会发生大振幅三维运动,前后链的运动十分复杂,前链处于极度张紧状态,后链则处于松弛状态;同时由于锚链系统受力大,刚变曲线会出现高度非线性的状态,甚至会超过平方关系很多;另外,由于运动是强非线性,各运动分量间有强烈的耦合,而且上浪等现象也会影响运动。在浅水情况下,附加质量及阻尼除了依赖于频率外,还与位置有关。本文针对上述问题,提出一个工程计算模型,一方面要进行简化,另一方面也保持一定的准确度。计算模型及流体作用力2对于油轮撤离后,在浅水域中处于生存工况下的多锚链的浮筒系泊系统(图1),现建立其三维六自由度的非线性计算模型,应用时域模拟来获得系统的运动情况。211系泊链三维动力学方程\n海洋工程第15卷2系统中系泊链有6条(或8条),均有足够的长度,在任何时刻都不出现拔桩现象。因此,系泊链可分为悬链部分和触底的平直部分,海底的摩擦相对影响较小,可忽略不计。另外,假设海流是定常的,不随深度变化,且没有垂直向分量。如图2所示,以悬链的触地点为原点,建立直角坐标系OXYZ,OZ轴垂直向上,___OXY平面位于海底,i,j,k为单位矢量。___设,u,v,w为悬链任意点P处的一组点处的悬_直角坐标单位矢量,其中u为P__链切向,Υ为水平面与u之间的夹角,Ω为u_在水平面上投影与矢量i之间的夹角,于图1悬链腿系泊系统图2地面及悬链上的坐标系是悬链单位向量组与地面单位向量组有下述关系__cosΥsinΩj+__sinΥk_u=cosΥcosΩi+__v=-sinΩi+cosΩj_(1)___w=-sinΥcosΩi-sinΥsinΩj+cosΥk_设dsu是位于P点处长度为ds的悬链元,它的长度在X,Y,Z方向上的投影为:©1994-2015ChinaAcademicJournalElectronicPublishingHouse.Allrightsreserved.http://www.cnki.net\n第1期浅水域生存工况下系泊浮筒系统三维运动3__dscosΥcosΩdx=dsuri=__(2)dy=dsurj=_dscosΥsinΩ_dz=dsurk=dssinΥ悬链拉伸后的长度ds’可表为ds’=ds(1+Ε),其中Ε=TƒEA,这里T为链张力,E为弹性模量,A为截面积,根据牛顿定律,悬链的三维动力学方程可写为:52x5T5Υ5t2=5scosΥ-TsinΥ5s+FucosΥ(1+Ε)-FwsinΥ(1+Ε)M52y5ΩM5t2=-TcosΩ5s-Fv(1+Ε)(3)52z5T5Υ5t2=5ssinΥ+TcosΥ5s+FusinΥ(1+Ε)+FwcosΥ(1+Ε)-MWc5xcosΥcosΩ(1+Ε)(4)5s=5ycosΥsinΩ(1+Ε)(5)5s=5z5s=sinΥ(1+Ε)(6)Ε=TƒEA(7)其中M为单位链长的质量(包括附加质量),Wc为单位链长重力与浮力之差,即有效重力,__Fu为切向阻力,Fv及Fw为相对于方向v及w的法向阻力。设流体相对于链单元的相对速度为:___Uzk_U=Uxi+Uyj+(8)则Fu=1ΘCDTΠDc(UxcosΥcosΩ+UycosΥsinΩ+UzsinΥ)|r|(9)2Fv=1ΘCDNDc(-UxsinΩ+UycosΩ)|r|(10)2Fw=1ΘCDNDc(-UxsinΥcosΩ-UysinΥsinΩ+UzcosΩ)|r|(11)2其中CDT为悬链切向阻力系数,CDN为法向阻力系数,Dc为链直径。|·|表示同式中的括号表达式的绝对值。在浅水、低频工况下,悬链振荡主要表现为垂荡,而且垂向惯性力与总链力相比,只占很小一部分。例如,在后面的例A中,考虑悬链端部随波而动时,其松弛链的惯性力占总链力13%,张紧链的惯性力占其总链力的7%以下。因此,作为一个简化,我们将略去链惯性力的影响,这样做基本能满足工程估算精度的需要,又可节省大量计算时间。如果要进一步提高精度,加入惯性力的影响,则可采用如下的近似。在拟静态位移求出后,耦合浮筒的运动时间∃t,近似求出悬链的加速度,以及相应的由惯性力所产生的张力的增量:©1994-2015ChinaAcademicJournalElectronicPublishingHouse.Allrightsreserved.http://www.cnki.net\n海洋工程第15卷4rrXrrYrrZ∃TX∃TY∃TZA11A12A13A12A22A23A13A23A33(12)=上式只计及法向加速度的影响,质量矩阵[Aij]各分量为:mi+ΘCMdsA(1-cos2Ωcos2Υ)mi+ΘCMdsA(1-sin2Ωcos2Υmi+ΘCMdsAcos2ΥA11=A22=A33=(13)ΘCMdsAsinΩcosΩsin2ΥΘCMdsAcosΩsinΥcosΥΘCMdsAsinΩsinΥcosΥA12=-A13=-A23=-而加速度采用如下差分计算:rrx=1(xj+1+xj-1-2xj)∃t21rry=(yj+1+yj-1-2yj)(14)∃t21rrz=(zj+1+zj-1-2zj)∃t22.2浮筒运动方程本文中,假设风、波、流是同向的,且与OXY平面成Ηw角。考虑浮筒的六自由度运动,其动力学方程组可简写为如下的矩阵形式:rrXrrYrrZrrΑrrΒrrΧFXm+m11000mzG+m150FY0m+0-mzG+00m12m24FZ00m+m33000=FΑ0-mzG+0I44+m4400m24FΒmzG+000I55+m550m15FΧ(15)00000I66其中mij为附加质量,(X,Y,Z)为线位移,(Α,Β,Χ)为角位移,FX,矩),含括流体作用力,恢复力,重力,以及悬链系泊力等。为相应的力(力,FΑ在一般情形下,风力的影响较小,但在生存工况下,风力的大小已达到波流力的量级,不能忽视,我们将风力表示为:__FWDX=1ΘaCDWDA3VWD|VWD|cosΗW2__FWDY=1ΘaCDWDA3VWD|VWD|sinΗW(16)2FWDZ=0©1994-2015ChinaAcademicJournalElectronicPublishingHouse.Allrightsreserved.http://www.cnki.net\n第1期浅水域生存工况下系泊浮筒系统三维运动5_式中Θa为空气密度,CDWD为风阻力系数,A3为受风侧面积,VWD为相对风速。由于在生存工况下,浮筒运动振幅很大,A3实际变化很大,因此,A3将不按平均值计算,而是按瞬时的受风面积计算。其最大值等于浮筒的侧面积。风也会对角运动有影响,但为了简化情况,将它归纳到波流力矩中一并考虑。浮筒的重力为mg,考虑到浮筒在生存工况下会有大倾角运动,我们取恢复力(矩)为:2Α)FBΑ=-mgrGMrΑ(1-22Β)FBΒ=-mgrGMrΒ(1-(17)2DBFBZ=ΘrgΠ(2)rA2其中垂向恢复力FBZ中的A按实际瞬时的浸水深度处理,其最大值等于浮筒的型深。DB为浮筒的直径。考虑到在浅水域中,主要是低频长波起作用,绕射效应相对较小,对链张力影响最大的将是由流与波产生的水平阻尼力,它们可表示为:FDX=1Θ0CDXDBAVx|Vx|2(18)FDY=1Θ0CDYDBAVy|Vy|2其中Vx,Vy是水相对浮筒质心的相对运动速度:Vx=Vwx+Vcx-Vy=Vwy+Vcy-xαyα(19)在浅水域中,由于浮筒与海底的间隙较小,因而CDX,CDY将比深水中的值要大7浪产生的垂向阻尼力可表为:。由波FDZ=1Θ0DDZΠ()2Vz|Vz|DB(20)22其中Vz为相对速度:zα(21)Vz=Vwz-由于浮筒是一个圆形扁平体,几乎是随浪运动,相对速度Vz很小,故FDZ一般不大。但考虑到浮筒运动到最高点时,这时一般会受到上波影响,等价于受到一个向下的外力。当浮筒运动到最低点时,由于浅水的影响,附加质量变大,亦等价于有一个向上的外力作用。综合这些因素到FDZ中,系数CDZ就可能要取十分大的值。在后面的例A中,流速高、波高相对较小,取CDZ=5。在例B中,流速较低,而波高相对较大,取CDZ=10。对于系泊浮筒的运动,主要影响来自链力及与水平线运动的耦合。对于自由漂浮的浮筒,在低频波与风、流共同作用下,倾角仍大致保持与波面倾角相一致,即扰动力矩主要来自波动扰动。另外,由于角运动自振频率相对较高,可以认为不会与入射波共振,因此,我们取粘性阻尼力矩为线性形式。FDΑ=-CDΑΑαrFDΒ=-CDΒΒrFDΧ=-CDΧΧ(22)©1994-2015ChinaAcademicJournalElectronicPublishingHouse.Allrightsreserved.http://www.cnki.net\n海洋工程第15卷6而风、波、流共同扰动力矩筒化取为与线性波扰动力矩相接近的形式:FWΑ=AΑ1sinΞt+AΑ2sin3ΞtcosΗwFWΒ=AΒ1sinΞt+AΒ2sin3ΞtsinΗwFWΧ=0其中sin3Ξt项,主要考虑由于上浪及波浪破碎等原因带来的高频影响。(23)对于链力,我们由链上端位移,分别用射的法求解悬链方程,从而求得各系泊链的拉力。算例3算例A311(1)环境条件水深28.4m,风速45mƒs,流速2.3mƒs,波振幅7.1m,波周期10.2s。(2)浮筒参数自重2850kN,型深5.0m,直径12m,重心高度2m,吃水3.3m。(3)链参数链6条,在360°范围内对称分布,单位链长在水中的重量为2.480m等价直径0.1m,预张力90kN。(4)链系刚度曲线06kNƒm。每条链总长为与实际情况拟合,先由悬链线理论求得水平刚度曲线,然后再乘上修正因子X(1+)。5.0(5)水动力参数m11=m22=300t,m15=-100kNrm,AΑ1=AΒ1=m33=475t,m44=m55=420trm2,m66=0m24=100trm,CDX=CDY=2.5,CDZ=5600kNrm,AΑ2=AΒ2=-200kNrm算例B312(1)环境条件水深22.5m,风速85mƒs,流速1mƒs,波振幅8.9m,波周期14.3s。(2)浮筒参数自重1700kN,型深3.66m,直径11.5m,重心高度1.6m,吃水1.77m。(3)锚链参数链6条,在360°范围内对称分布,单位链长在水中的重量为1.445m,等价直径0.08m,预张力80kN。(4)链系刚度曲线356kNƒm,每条链总长为与实际情况拟合,先由悬链线理论求得水平刚度曲线,然后再乘上修正因子X(1+)。3.0(5)水动力参数©1994-2015ChinaAcademicJournalElectronicPublishingHouse.Allrightsreserved.http://www.cnki.net\n第1期浅水域生存工况下系泊浮筒系统三维运动7m11=m22=170t,m33=450t,m44=m55=400trm2,m66=0CDZ=10m15=-160trm,m24=160trm,CDX=CDY=1.8,AΑ1=AΒ1=100kNrm,AΑ2=AΒ2=-37kNrm计算结果及讨论4411夹角ΗW的影响为了比较风、波、流与XOZ平面的夹角不同时,浮筒运动响应及链力的变化,取ΗW=0°,15°及90°(等价于30°)三种情况进行计算,限于篇幅,只给出了算例A(3a)至图(3f),图(4a)至图(4f),图(5a)至图(5f)。的部分结果,见图图3©1994-2015ChinaAcademicJournalElectronicPublishingHouse.Allrightsreserved.http://www.cnki.net\n海洋工程第15卷8图4由上述结果可以看出,随ΗW的增加(不超过30°)主受力链的最大链力从2400kN(ΗW=0°),2240kN(ΗW=15°),一直下降到1660kN(ΗW=30°,等价于90°)。上述计算结果与实验结果接近,当ΗW=0°时,最大链力的实验值为2300kN,当ΗW=30°时,实验值为1780kN,这表明本计算模型具有一定的精度。同时,可以认为,如果只需了解最大链力,则只要计算ΗW=0°这个工况,此工况可化为平面问题,使计算量大为减小。©1994-2015ChinaAcademicJournalElectronicPublishingHouse.Allrightsreserved.http://www.cnki.net\n第1期浅水域生存工况下系泊浮筒系统三维运动9图5412系泊链刚度的影响为了考虑系泊链刚度对最大链力的影响,选取二种刚度的系泊链(ΗW=下面给出算例A的部分结果。0°)进行计算,图(6a)至图(6c)为算例A在刚度EA=1000000.0t·kN图(7a)至图(7c)为算例A在刚度EA=2000000.0t·kN的计算结果。的计算结果。由上述结果可以看出,无论对哪一种系统及工况,增大系泊链的刚度,都会使主系泊链受力增大,纵荡最大值减小,但垂荡则变化不大。©1994-2015ChinaAcademicJournalElectronicPublishingHouse.Allrightsreserved.http://www.cnki.net\n海洋工程第15卷10图6图7结论5本文给出了一个浅水域中,多锚链浮筒系泊系统在生存工况下的受力及运动的工程计算模型。从计算的结果与部分实验结果的比较来看,该计算模型具有一定的精度。但该模型中的水动力计算模式,部分取自于实验的结果,或计算的经验,如何从理论上给出水动力计算的模式,将是我们进一步要研究的课题。©1994-2015ChinaAcademicJournalElectronicPublishingHouse.Allrightsreserved.http://www.cnki.net\n第1期浅水域生存工况下系泊浮筒系统三维运动11参考文献123李远林、吴永鸣,多锚链系统浮筒非线性漂移运动时域模拟,海洋工程,1990,Vol.8,No.1庄司,系泊浮体的运动及其系泊链的张力的研究,日本造船学会论文集,1976,No.138WataruKoterayama,EffectsofHydrodynamicForcesactingonColdWaterPipeandMooringLineonMotionsofOTECPlatform,西部造船学会会报,1985,No.72刘应中等,船舶在波浪中大幅度运动的工程算法,水动力学研究与进展,1995,Ser.A,Vol.10,No.2王涛、李家春等,波流相互作用对水动力系数的影响,水动力学研究与进展,1995,Ser.A,Vol.10,No.5M.IsaacsonandY.T.Ng,Time2DomainSecond2orderwaveInteractionwiththree2DimensionalFloat2ingBodies,Int.J.ofoffshoreandPolarEng.,1995,Vol.5,No.3邢至庄等,接近海底水平管的波浪力和CD,CM,CL值的实验研究,海洋工程,1990,Vol.8,No.34567THREE2DIMENSIONALMOTIONOFMULTI2CHAINMOORINGBUOY2SYSTEMINSHALLOWWATERANDSURVIVALCONDITIONZhangTingSunMingguang(ZhongshanUniversity,Guangzhou510275)AbstractAnEngineeringComputationalModelforthree2dimensionalMotionofmulte2chainmooringBuoy2systeminshallowwaterandsurvivalconditionisgiveninthispaper.Shooting2aimmethodisem2ployedforsolvingthedynamicalequationsofchainsystemandmatchedforthecomputationofbuoymo2tion.TheresponsesofBuoyandChainhavebeencomputedfordifferentwind2wave2currentdirectionsanddifferentrigidityofchain.Theresultsshowthatcomputationalmodelgivenbythispaperisreasonable.Keywordssurvivalcondition,shallowwater,buoy,chainsystem,three2dimensionalmotion©1994-2015ChinaAcademicJournalElectronicPublishingHouse.Allrightsreserved.http://www.cnki.net