- 2022-09-27 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
101简谐运动的基本特征和表述、振动的相位、旋转矢量法
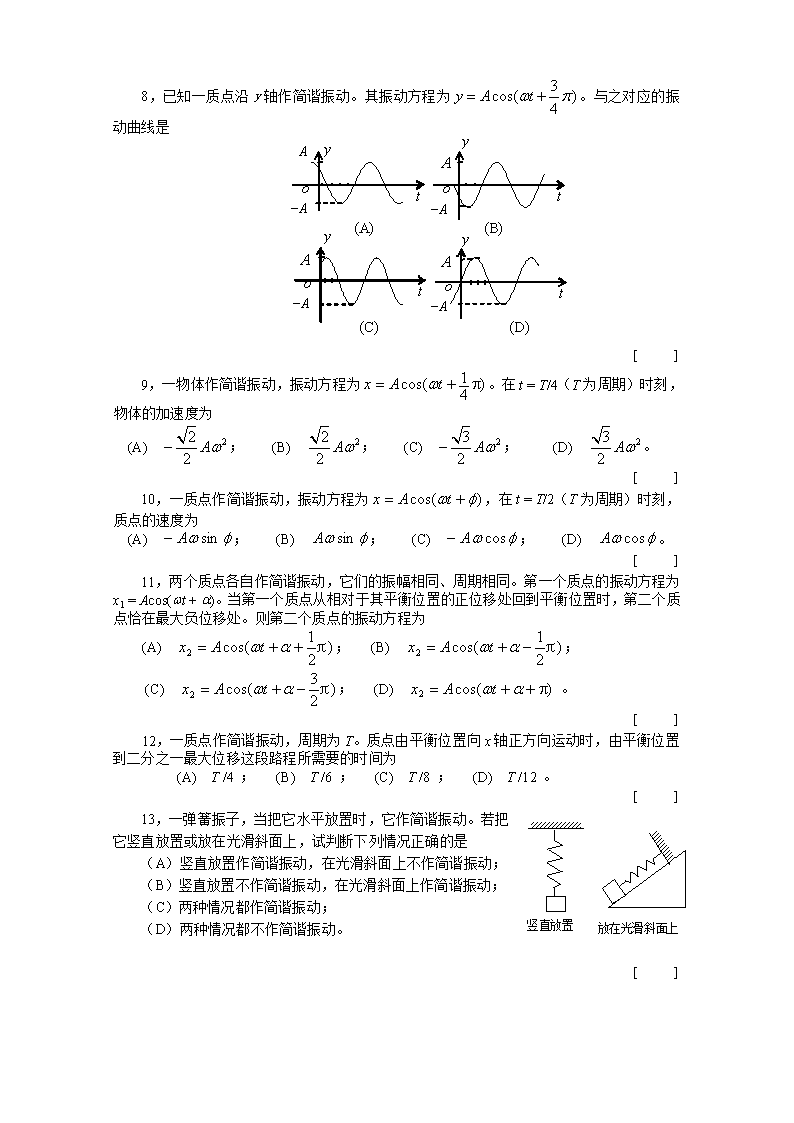
101简谐运动的基本特征和表述、振动的相位、旋转矢量法1.选择题1,物体做简谐运动时,下列叙述中正确的是(A)在平衡位置加速度最大;(B)在平衡位置速度最小;(C)在运动路径两端加速度最大;(D)在运动路径两端加速度最小。[]2,一弹簧振子,当时,物体处在(A为振幅)处且向负方向运动,则它的初相为(A);(B);(C);(D)。[]3,两个同周期简谐振动曲线如图所示。x1的相位比x2的相位(A)落后p/2;(B)超前p/2;(C)落后p;(D)超前p。[]4,把单摆摆球从平衡位置向位移正方向拉开,使摆线与竖直方向成一微小角度q,然后由静止放手任其振动,从放手时开始计时。若用余弦函数表示其运动方程,则该单摆振动的初相为(A)p;(B)p/2;(C)0;(D)q。[]5,一弹簧振子,当时,物体处在(A为振幅)处且向负方向运动,则它的初相为(A);(B);(C);(D)。[]6,一质点作简谐振动,振幅为A,在起始时刻质点的位移为,且向x轴的正方向运动,代表此简谐振动的旋转矢量图为[]7,一质点作简谐振动,周期为T。当它由平衡位置向x轴正方向运动时,从二分之一最大位移处到最大位移处这段路程所需要的时间为(A)T/12;(B)T/8;(C)T/6;(D)T/4。[]\n8,已知一质点沿y轴作简谐振动。其振动方程为。与之对应的振动曲线是[]9,一物体作简谐振动,振动方程为。在t=T/4(T为周期)时刻,物体的加速度为(A);(B);(C);(D)。[]10,一质点作简谐振动,振动方程为,在t=T/2(T为周期)时刻,质点的速度为(A);(B);(C);(D)。[]11,两个质点各自作简谐振动,它们的振幅相同、周期相同。第一个质点的振动方程为x 1=Acos(wt+a)。当第一个质点从相对于其平衡位置的正位移处回到平衡位置时,第二个质点恰在最大负位移处。则第二个质点的振动方程为(A);(B);(C);(D)。[]12,一质点作简谐振动,周期为T。质点由平衡位置向x轴正方向运动时,由平衡位置到二分之一最大位移这段路程所需要的时间为(A)T/4;(B)T/6;(C)T/8;(D)T/12。[]13,一弹簧振子,当把它水平放置时,它作简谐振动。若把它竖直放置或放在光滑斜面上,试判断下列情况正确的是(A)竖直放置作简谐振动,在光滑斜面上不作简谐振动;(B)竖直放置不作简谐振动,在光滑斜面上作简谐振动;(C)两种情况都作简谐振动;(D)两种情况都不作简谐振动。[]\n14,图中三条曲线分别表示简谐振动中的位移x、速度v和加速度a。下列说法中哪一个是正确的?(A)曲线3,1,2分别表示x,v,a曲线;(B)曲线2,1,3分别表示x,v,a曲线;(C)曲线1,2,3分别表示x,v,a曲线;(D)曲线2,3,1分别表示x,v,a曲线。[]15,一质点沿x轴作简谐振动,振动方程为(SI),从t=0时刻起,到质点位置在x=-0.02m处,且向x轴正方向运动的最短时间间隔为(A);(B);(C);(D)。[]16,一质点在x轴上作简谐振动,振幅A=4cm,周期T=2s,其平衡位置取作坐标原点。若t=0时刻质点第一次通过x=-2cm处,且向x轴负方向运动,则质点第二次通过x=-2cm处的时刻为(A)1s;(B)s;(C)s;(D)2s。[]17,一质点做简谐振动,其位移x与时间t的关系如图所示。在s时,质点的(A)速度为正的最大值,加速度为零;(B)速度为负的最大值,加速度为零;(C)速度为零,加速度为负的最大值;(D)速度为零,加速度为正的最大值。[]18,一个弹簧振子,第一次用力把弹簧压缩x后开始振动,第二次把弹簧压缩2x后开始振动,则两次振动的最大加速度的大小之比为(A);(B);(C);(D)。[]19,一小球作周期为0.5s、振幅为10cm的简谐运动,则在正方向的最大位移处,小球运动的加速度为(A)0;(B)-15.8m/s2;(C)15.8m/s2;(D)-1.26m/s2。[]20,用余弦函数描述一简谐振动。已知振幅为A,周期为T,初相,则振动曲线为:\n[]2.判断题1,点离开平衡位置的位移随时间按正弦或余弦函数发生变化,则该质点作简谐运动。2,个作简谐运动的物体,从负方向的最大位移处运动到正方向的最大位移处所需的时间为一个周期。3,一个简谐运动的振幅A、角频率ω和初相φ都给定了,则这个简谐运动在任意时刻的运动状态就完全确定了。4,点作简谐振动时,从平衡位置运动到最远点需时1/4周期,因此走过该距离的一半需时1/8周期。5,一个作简谐振动的物体,其位移与加速度的相位始终相差p。6,个作同频率简谐振动的质点,质点1的相位比质点2的相位超前p/2。则当第一个质点在负的最大位移处时,第二个质点恰好在平衡位置处,且向正方向运动。7,一质点作匀速圆周运动,它在直径上的投影点的运动是简谐振动。8,个作简谐振动的物体处于平衡位置处时具有最大的速度和最大的加速度。9,弹簧振子做简谐振动,周期为T,若t时刻和t+△t时刻的位移大小相等,运动方向也相同,则△t一定等于T的整数倍。10,弹簧振子做简谐振动,周期为T,则在t时刻和t+T/2时刻弹簧的长度一定相等。11,做简谐振动时,其加速度的大小与物体相对平衡位置的位移成正比,方向始终与位移方向相反,总指向平衡位置。12,体做简谐运动时,其速度的大小和方向、加速度的大小和方向都在随时间变化。13,\n个质点作同频率的简谐振动,当第一个质点自正方向回到平衡位置时,第二个质点恰在振动正方向的端点,则第二个质点的相位超前p/2。3.填空题1,一物体作简谐振动,周期为T,则物体由平衡位置运动到最大位移处所需的时间为。2,一弹簧振子作简谐振动,其运动方程用余弦函数表示。若t=0时,振子在负的最大位移处,则初相为____________。3,一弹簧振子作简谐振动,其运动方程用余弦函数表示。若t=0时,振子在位移为A/2处,且向负方向运动,则初相为。4,一物体作简谐振动,周期为T,则物体由正的最大位移处运动到负的最大位移处所需的时间为。5,两个小球A、B做同频率、同方向的简谐振动,当A球自正方向回到平衡位置时,B球恰好在正方向的端点,则A球比B球(填“超前”或“落后”)p/2。6,图中用旋转矢量法表示了一个简谐振动。旋转矢量的长度为0.04m,旋转角速度w=4prad/s。此简谐振动以余弦函数表示的振动方程为x=__________________________(SI)。7,一水平弹簧简谐振子的振动曲线如图所示。当振子处在位移为零、速度为-wA、加速度为零的状态时,对应于曲线上的点。8,一质点沿x轴作简谐振动,振动范围的中心点为x轴的原点。已知周期为T,振幅为A。若t=0时质点处于处且向x轴正方向运动,则振动方程为x=。9,一水平弹簧简谐振子的振动曲线如图所示。当振子处在位移的绝对值为A、速度为零、加速度为-w2A的状态时,对应于曲线上的__________点。\n10,一物体作简谐振动,其振动方程为(SI)。当t=0.6s时,物体的速度v=__________________。11,一简谐振动的表达式为,已知t=0时的初位移为0.04m,初速度为0.09m/s,则其振幅A=_____________。12,一质点作简谐振动的角频率为w、振幅为A。当t=0时质点位于处,且向x正方向运动。试画出此振动的旋转矢量图。13,已知简谐振动曲线如图所示,则用余弦函数表示的振动方程为x=________________。14,已知两个简谐振动的振动曲线如图所示。两简谐振动的最大速率之为。15,一简谐振子的振动曲线如图所示,则以余弦函数表示的振动方程为_________________________。16,已知一个简谐振动的振幅A=2cm,角频率w=4prad/s,以余弦函数表达运动规律时的初相。试画出位移和时间的关系曲线(振动曲线)。\n17,一单摆的角振幅,周期s,则其最大的摆动角速度的大小为。18,一简谐振动曲线如图所示,则由图可确定在t=2s时刻质点的速度为______________。19,两个弹簧振子的周期都是0.4s,设开始时第一个振子从平衡位置向负方向运动,经过0.5s后,第二个振子才从正方向的端点开始运动,则这两振动的相位差为___________。20,一质点在x轴上做简谐振动,振幅A=4cm,周期T=2s,其平衡位置取作坐标原点。若t=0时刻质点第一次通过x=-2cm处,且向x轴正方向运动,则质点第二次通过x=-2cm处的时刻为。1~5CABCD6~10BCBBB11~15ADCCD16~20BCCBA1~5对错对错对6~10错对错错错11~13对对错1、;2,p;3,p/3;4、;5、超前;6、;7、b,f;8、;9、a,e;10、-0.209m/s;11、0.05m;12,答案:见图13,;14,1∶1;15,答案:;16,答案:见图17:0.394rad/s;18:9.42cm/s;19:p;20:1.33s。查看更多