《理论力学》第十章 质心运动定理 动量定理 习题

《理论力学》第十章 质心运动定理 动量定理 习题

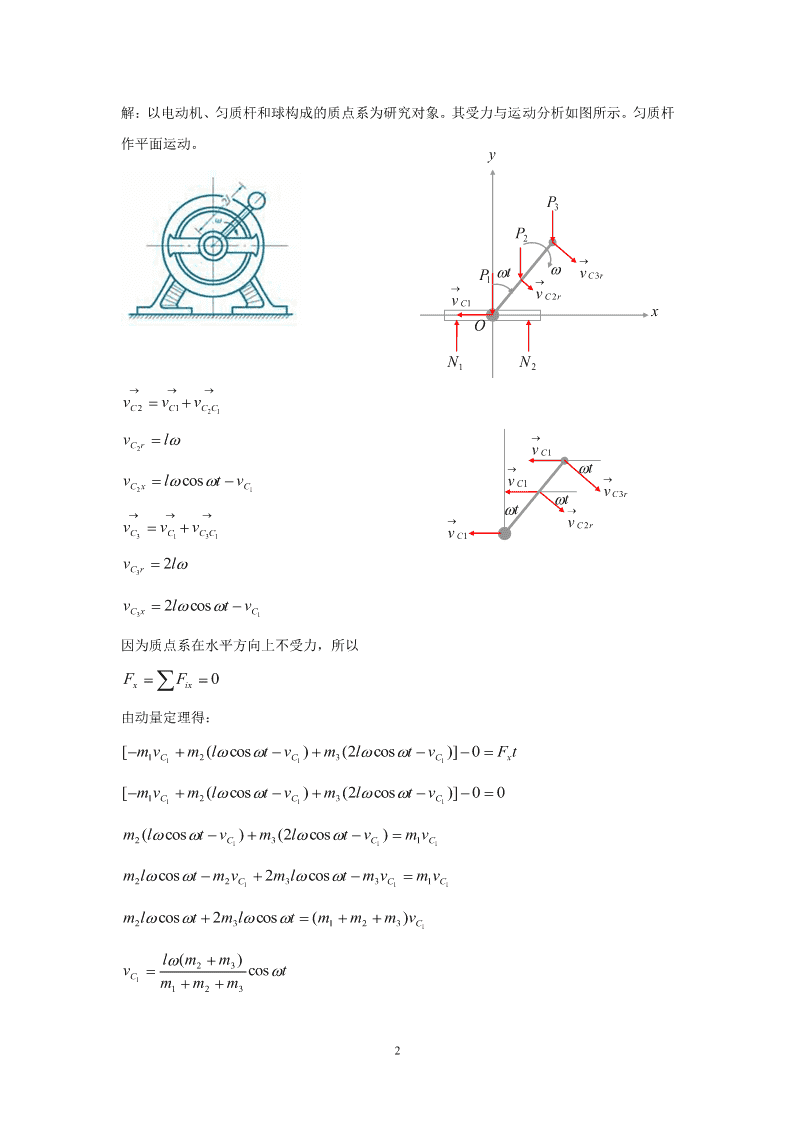
第十章质心运动定理动量定理习题解[习题10-1]船A、B的重量分别为2.4kN及1.3kN，两船原处于静止间距6m。设船B上有一人，重500N，用力拉动船A，使两船靠拢。若不计水的阻力，求当两船靠拢在一起时，船B移动的距离。解：以船A、B及人组成的物体系统为质点系。因为质点系在水平方向不受力。即：Fix0，y设B船向左移动了S米，则A船向右移动了6－S米。由质点系的动量定理得：[mv－(mm)v]－0＝FtAAB人BxABOxx6m[mv－(mm)v]＝00AAB人Bmv(mm)vAAB人Bymv(mm)vAAB人B6ssm(mm)AB人ttm(6s)(mm)sABAB人Ox6ss2.4(6s)(1.30.5)s2.4(6s)(1.30.5)s4(6s)3s24s3.43(m)7[习题10-2]电动机重P，放置在光滑的水平面上，另有一匀质杆，长2L，重P，一端与12电动机机轴固结，并与机轴的轴线垂直，另一端则刚连一重P的物体，设机轴的角速度为3（为常量），开始时杆处于铅垂位置并且系统静止。试求电动机的水平运动。1\n解：以电动机、匀质杆和球构成的质点系为研究对象。其受力与运动分析如图所示。匀质杆作平面运动。yP3P2tPvC3r1vC2rvC1xON1N2vvvC2C1C2C1vlC2rvC1tvlcostvvC1C2xC1vC3rttvvvvC2rC3C1C3C1vC1v2lC3rv2lcostvC3xC1因为质点系在水平方向上不受力，所以FxFix0由动量定理得：[mvm(lcostv)m(2lcostv)]0Ft1C12C13C1x[mvm(lcostv)m(2lcostv)]001C12C13C1m(lcostv)m(2lcostv)mv2C13C11C1mlcostmv2mlcostmvmv22C133C11C1mlcost2mlcost(mmm)v23123C1l(mm)23vcostC1mmm1232\ndxC1l(m2m3)costdtmmm123l(mm)23dxcostdtC1mmm123l(mm)23xcostdtC1mmm123l(mm)23xcostd(t)C1mmm123l(mm)23xsintC1mmm123l(PP)23xsintC1PPP123这就是电动机的水平运动方程。[习题10-3]浮动起重机起吊重P20kN的重物，起重机重P200kN，杆长OA8m，120开始时杆与铅垂位置成60角，忽略水的阻力，杆重不计，当起重杆OA转到与铅垂位置成030角时，求起重机的位移。A解：以重物和起重机构成的物体系统为质系。因为质点系在水平方向不受力，所以F0xy0d(mv)30CxF0xPdx1xOPv＝const2Cxv|＝const0Cxt0qbv＝0abCxdxC0dtx＝const。即OA运动前后，质点系的质心保持不变。也就是质心守恒。C0当OA杆转到与铅垂位置成30角时，质点系质心的横坐标为：3\nmxmx1C12C2xC1mm120b20(8cos60a)200(a)PxPx1C12C22xC1PP202001220a80200a100bxC1220220a100b80xC122011a5b4xC1110当OA杆转到与铅垂位置成30角时，质点系质心的横坐标为：0b20(8cos30c)200(c)PxPx1C12C22xC2PP202001220c803200c100bxC2220A220c100b803y600xC2P2201xOP211c5b43xC211q因为质心守恒，所以bcbxx，即：C1C211a5b411c5b43111111a5b411c5b4311a411c4311(ca)4(31)4(ca)(31)0.2662(m)114\n0故，当起重杆OA转到与铅垂位置成30角时，起重机向左移动了0.2662米。[习题10-4]匀质圆盘绕偏心轴O以匀角速度转动。重P的夹板借右端弹簧推压面顶在圆盘上，当圆盘转动时，夹板作住复运动。设圆盘重W，半径为r，偏心距为e，求任一瞬时作用于基础和别螺栓的动反力。解：设机座的重量为G，则当偏心轮转动时，质点系的受力如图所示。当停偏心轮静止时，水平约束力不存在，此时的反力为静反力：FWPG；当偏心轮转动时，存在N动反力：F和F。质点系的受力与运动分xyW析如图所示。vPC1re当偏心轮转动时，偏心轮的动量为：CvCt12xOC2WWePv1C1ggGC3当偏心轮转动时，夹板的动量为：FPxPv2C2gFyFN因为夹板作平动，所以其质心的速度等于夹板与偏心轮的切点的速度。切点的运动方程为：xeecostv0e(sint)esint，即：xvesint，故：C2PPesintPv2C2gg当偏心轮转动时，机座的动量为：GGPv002C3gg质点系的动量为：5\nPPPP123WesintPesint(WP)esintPPPP0x1x2x3xgggWecostWecostPPPP00y1y2y3yggdPxFFWPGxNdt式中，FWPG，故：N2d(WP)esinte(WP)costWP2F[]ecost，即：xdtgggWP2FecostxgdPyFydtdP2ydeWcosteWsintW2F()ecost，即ydtdtgggWP2Fecostxg[习题10-5]大直角锲块A重P，水平边长为a，放置在光滑水平面上；小锲块B重Q，水平边长为b（ab），如图放置在A上，当小锲块B完全下滑至图中虚线位置时，求大锲块的位移。假设初始时系统静止。解：建立如图所示的坐标系。由于质点系在水平方向不受力，即F0，所以：xbmaF0BCxxa0CxAadvC0dt6\nvCC1yv|C0，故：bCt01Bv0CAadxxC0dtxconst，即质心守恒：CxxyC1C2PaQ2bg3g3Pa2bQxC1PQPQ3(PQ)bBggAaxsabP(s)Q(as)33xC2PQP(a3s)Q(3a3sb)xC23(PQ)Pa3Ps3Qa3QsQbx，故：C23(PQ)Pa2bQPa3Ps3Qa3QsQb3(PQ)3(PQ)2bQ3(PQ)s3QabQ3(PQ)s3Qa3bQ(ab)Qs（A锲块各左移动的位移）PQ[习题10-6]匀质杆AB长2l，其B端搁置于光滑水平面上，并与水平成0角，当杆倒下时，求杆端A的轨迹方程。解：由于AB杆在水平方向上不受力，所以其质心的x坐标守恒。即：xxlcosCtC007\n质心C沿xlcos直线向下运动。y0A设任意时刻A的坐标为A(x,y)，则：xlcoslcosC00xxlcoslcosB0Ny2lsinAylsiny2消去得：2y2(xlcos)()l，为一椭圆。A(x,y)02CxBNA0[习题10-7]图示系统中，m4kg，m2kg，30。设当A在斜面上作无初速地AC向下滚过40cm时，斜面在光滑的水平面上移过20cm。求B的质量。yyAABCBCmgmgAAmgmgmgBCmgCBxx203N1N2N1N2aab20bcc解：以A、B、C构成的质点系为研究对象，其受力如图所示。因为水平方向不受力，所以aCx0，即：8\ndvCx0dtvCCx1v|C0，故：Cxt01v0CxdxCconst，即质心守恒：dtxxC2C12bmamm(bc)ACB3xC1mmmABC2b4b4a2m(bc)4am(bc)BB33xC142m6mBB2b4(a20203)2(20)m(bc20)B3xC242mB4b4a8080340m(bc)20mBB3xC242mB4b4a120803m(bc)20mBB3x，由xx得：C2C2C142mB4b4b4am(bc)4a120803m(bc)20mBBB336m6mBB012080320mB0643mBm4360.928(kg)B9\n[习题10-8]质量为m，半径为R的匀质半圆板，受力偶作用在铅垂面内绕O轴转动，转动的角速度为，角速度为。C点为半圆板的质心，当OC与水平线成任意角时，求此4R瞬时轴O约束力（OC）。3解：在法向应用牛顿第二定理得：FMOxmaFFsinFcosmgsinnnyxFyC2mOCFysinFxcosmgsinvCmg24RmFsinFcosmgsinyx324RmFsinFcosmgsinyx324RmFFcotmg…………(1)yx3sin质点系的动量：4RmPmvmOCC34RmPt3在切向应用动量定理得：dPtFtdtdPtFFcosFsinmgcostyxdtd4Rm()FcosFsinmgcosyxdt34RmdFcosFsinmgcosyx3dt4RmFcosFsinmgcosyx34RmFcosFsinmgcosyx34RmFFtanmg…………(2)yx3cos10\n(2)(1)得：24RmF(tancot)()x3cossin222sincos4RmsincosF()xcossin3cossin4Rm2F(cossin)x3上式代入（2）得：4RmFFtanmgyx3cos4RmFmgFtanyx3cos4Rm4Rm2sinFmg(cossin)y3cos3cos24Rm4Rm2sinFmg(sin)y3cos3cos24Rm2sinFmg(sin)y3coscos224Rm(sin1)sincosFmg[]y3cos224RmcossincosFmg[]y3cos4Rm2Fmg(sincos)y3[习题10-9]重2N的物体以5m/s的速度向右运动，受到按图示随时间变化的方向向左的力F/NF作用。试求受此力作和后，物体速度变为多大。120解：v5m/s（向右）16000tt[0,0.02]sF（向左）6000(0.04t)t[0.02,0.04]s根据动量定理得：t/(102s)0123411\ntmvmvFdtt001tvvFdtt0m0上式在水平方向（x轴）的投影为：10.020.04vv[6000tdt6000(0.04t)dt]t000.02m120.0220.04v5{3000[t]6000[0.04t0.5t]}t00.02m600020.0220.04v5{0.5[t][0.04t0.5t]}t00.02m6000222v5[0.50.02(0.040.040.50.04)(0.040.020.50.02)]t2/9.860009.80.0004v5t2v511.76tv6.76(m/s)，负号表示此时重物的速度方向左。t[习题10-10]在物块A上作用一常力F，使其沿水平面移动，已知物块的质量为10kg，F0与水平面的夹角30。经过5秒钟，物块的速度从2m/s增至4m/s。已知摩擦因数f0.15，试求F的大小。F解：物块A的受力如图所示。Axmg根据动量定理得：'FtmvmvFdtt00N上式在x轴上的投影为：500mvmv[Fcos30f(mgFsin30)]dtt0010(42)[F0.8660.15(109.8F0.5)]540.866F0.15(980.5F)40.866F14.70.075F0.941F18.7F19.87(N)12\n[习题10-11]计算下列刚体在图示已知条件下的动量。解：(a)图所示刚体的动量为：PPv0pv，方向与v相同。00g(a)(b)图所示刚体的动量为：PPpveCPggeC方向与垂直于OC，斜向下。O(c)图所示刚体的动量为：(b)ppp12v2C2pmvmaMaOBx1C113CaM112pmvmaMay2C222a2326vCC1211pMaiMaj36Aa224117pppMaMaxy9366(c)1杆BOA的总质量为Mpy60arctanarctanarctan0.2514.04p2x3(d)图所示刚体的动量为：pmvCO2xmgRCrvC(Rr)(Rr)vCvvcos[(Rr)]CxCyvvcos(Rr)cos(d)CxC13\nvvsin(Rr)sinCxCpmvimvjCxCypm(Rr)cosim(Rr)sinj[习题10-12]计算下列系统在图示已知条件下的动量。解：(a)dxvxAdtdxdBv[x(lr)sin]x(lr)cosBxdtdtyMgdydBv[(lr)cos](lr)sinBydtdtrAvAxdxdllvC(xsin)xcosOClMgCxxdtdt22mgrdydllBC(a)v(cos)sinCydtdt22pMvMxAxAp0AypMvM[x(lr)cos]BxBxPByMvByM(lr)sinlpmvm[xcos]CxCx2mlpmvsinCyCy2ppxipyjllp{Mxm(xcos)M[x(lr)cos]}i[msinM(lr)sin]j2214\n解：(b)yvvr滑块A作复合运动。aPt动点：AWv动系：固连于T字杆上的坐标系。leABtxO静系：固连于地面上的坐标系。C绝对速度：A相对于地面的速度。相对速度：A相对于T形杆的速度。牵连速度：T形杆中与A相重点滑块A的重量不计(b)（牵连点）相对于地面的速度。vvvaervvsintlsinteavvlsintCxev0CylxcostB2dxBdllv(cost)sintBxdtdt22lysintB2dyBdllv(sint)costBydtdt22ppxipyjWPlPlp(lsintsint)i(cost)jgg2g2P2WPplsintilcostj2g2g15\n解：(c)yA2P1lP2CP2llPD1ttxOB(c)质心运动方程速度动量xA0dxAP2vAx0pAx00dtgAyA2lsintdyAP2vAy2lcostpAy2lcostdtgxB2lcostdxBP2vBx2lsintpBx2lsintdtgByB0dyBP2vBy0pBy00dtgxlcostvlsint2PCCx1plsintCxgCyClsintvCylcost2P1plcostCygllxcostvsintPlDDx122pDxsintg2DllysintvcostPlDDy122pDycostg2ppxipyjP2PPP2PP211211p(02lsintlsintlsint)i(2lcost0lcostlcost)jgg2ggg2gP2PPP2PP211211p(2)lsinti(20)lcostjgg2ggg2g5P4P5P4P1212plsintilcostj2g2g16\n[习题10-13]质量为m的子弹A以速度v射入同向运动的质量为M、速度为v的物块BAB内，不计地面与物体之间的摩擦。求：（a）若子弹留在物块B内，则物块与子弹的共同速度u；（b）若子弹穿透物块并以u继续前进，则物块的速度u。AB解：（a）若子弹留在物块B内，求物块与子弹的共同速度u。由动量定理得：(mM)u(mvMv)Ft0t0ABxMvmvBAumM（b）若子弹穿透物块并以u继续前进，求物块的速度u。AB由动量定理得：(muMu)(mvMv)Ft0t0ABABxmuMu(mvMv)0ABABMvmvmuBAAuBM17