5.1点运动(热点题型)·数学中考分类精粹

5.1点运动(热点题型)·数学中考分类精粹

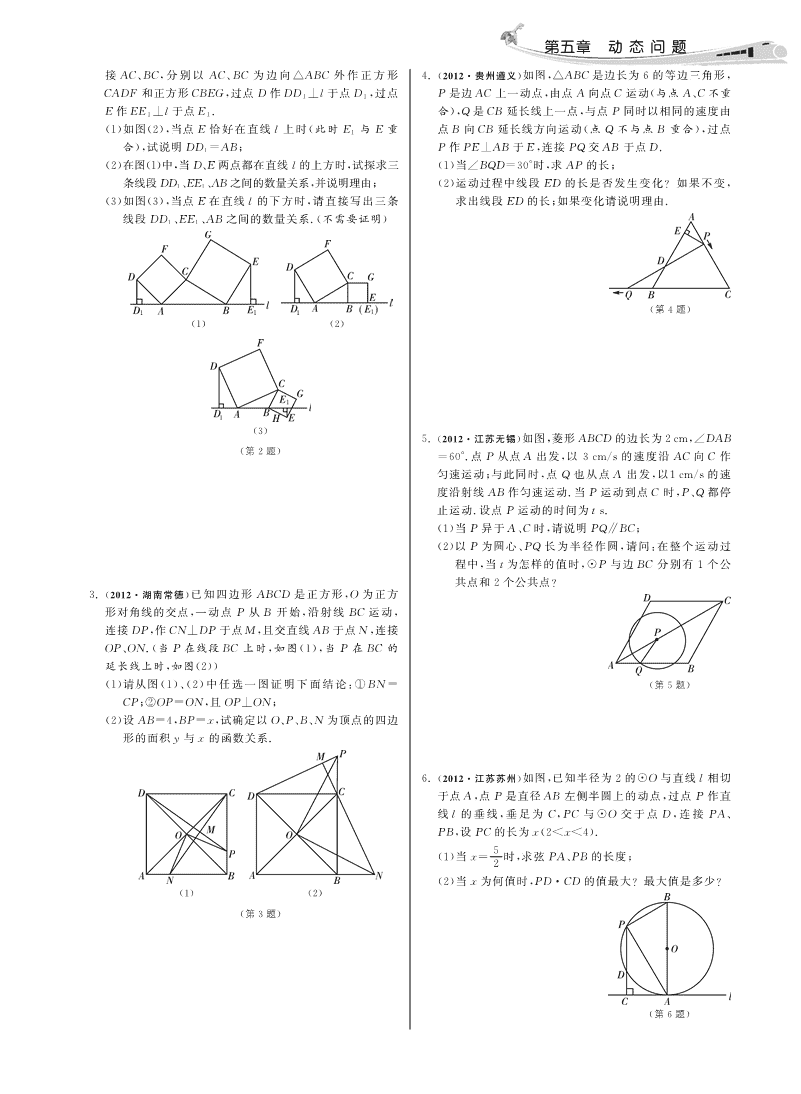
第五章动态问题§５．１点运动【题型概述】∴△BAD≌△CAF．用运动的观点来探究几何图形变化规律的问题称为动∴CF＝BD．态问题．此类问题的显著特点是图形中的某些元素(如点、∴CF＋CD＝BD＋CD＝BC＝AC．线)或整个几何图形按某种规律运动．本节研究点的运动．即①BD＝CF,②AC＝CF＋CD．点动型就是在三角形、矩形等一些几何图形上,设计一(２)AC＝CF＋CD不成立,AC、CF、CD之间存在的数量个或几个动点,并对这些点在运动变化的过程中产生的等量关系是AC＝CF－CD．关系、变量关系、图形的特殊状态、图形间的特殊关系等进行理由:由(１)知,AB＝AC＝BC,AD＝AF,∠BAC＝研究．∠DAF＝６０°,【典题演示】∴∠BAC＋∠DAC＝∠DAF＋∠DAC,【例１】(２０１２?四川内江)已知△ABC为等边三角形,即∠BAD＝∠CAF．点D为直线BC上的一动点(点D不与B、C重合),以AD∵在△BAD和△CAF中,为边作菱形ADEF(A、D、E、F按逆时针排列),使∠DAF＝AC＝AB,∠BAD＝∠CAF,AD＝AF,６０°,连接CF．∴△BAD≌△CAF．(１)如图(１),当点D在边BC上时,求证:①BD＝CF;∴BD＝CF．②AC＝CF＋CD;∴CF－CD＝BD－CD＝BC＝AC,(２)如图(２),当点D在边BC的延长线上且其他条件不即AC＝CF－CD．变时,结论AC＝CF＋CD是否成立?若不成立,请写出AC、(３)AC＝CD－CF．CF、CD之间存在的数量关系,并说明理由;理由:∵∠BAC＝∠DAF＝６０°,(３)如图(３),当点D在边BC的延长线上且其他条件不变∴∠DAB＝∠CAF．时,补全图形,并直接写出AC、CF、CD之间存在的数量关系．∵在△BAD和△CAF中,AB＝AC,∠DAB＝∠CAF,AD＝AF,∴△BAD≌△CAF．∴CF＝BD．∴CD－CF＝CD－BD＝BC＝AC,即AC＝CD－CF．(１)(２)【归纳交流】本题是一道单质点的运动问题．解决此类动点几何问题常常用的是“类比发现法”,也就是通过对两个或几个相类似的数学研究对象的异同进行观察和比较,从一个容易探索的研究对象所具有的性质入手,去猜想另一个或几个类似图形所具有的类似性质,从而获得相关结论．(３)【例２】(２０１２?贵州六盘水)如图(１),已知△ABC中,【思路点拨】(１)根据已知得出AF＝AD,AB＝BC＝AC,AB＝１０cm,AC＝８cm,BC＝６cm．如果点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C∠BAC＝∠DAF＝６０°,求出∠BAD＝CAF,证匀速运动,它们的速度均为２cm/s．连接PQ,设运动的时间△BAD≌△CAF,推出CF＝BD即可;(２)求出∠BAD＝∠CAF,根据SAS证△BAD≌△CAF,为t(单位:s)(０≤t≤４)．解答下列问题:推出BD＝CF即可;(３)画出图形后,根据SAS证△BAD≌△CAF,推出CF＝BD即可．【完全解答】(１)∵四边形AFED是菱形,∴AF＝AD．∵△ABC是等边三角形,(１)(２)∴AB＝AC＝BC,∠BAC＝６０°＝∠DAF．(１)当t为何值时,PQ∥BC;∴∠BAC－∠DAC＝∠DAF－∠DAC,(２)设△AQP面积为S(单位:cm２),当t为何值时,S取即∠BAD＝∠CAF．得最大值,并求出最大值;∵在△BAD和△CAF中,(３)是否存在某时刻t,使线段PQ恰好把△ABC的面积AB＝AC,∠BAD＝∠CAF,AD＝AF,平分?若存在,求出此时t的值;若不存在,请说明理由;\n(４)如图(２),把△AQP沿AP翻折,得到四边形(４)假设存在时刻t,使四边形AQPQ′为菱形,则有AQPQ′．那么是否存在某时刻t,使四边形AQPQ′为菱形?AQ＝PQ＝BP＝２t．若存在,求出此时菱形的面积;若不存在,请说明理由．【思路点拨】这是一个动态几何问题,综合性程度高,但我们只要仔细观察、冷静思考、多读几遍题目就会找到解决问题的突破口,千万不能轻易放弃．(１)由PQ∥BC时的比例线段关系,列一元一次方程求解;(２)如解答图(１)所示,过点P作PD⊥AC于点D,构造(２)比例线段,求得PD,从而可以得到S的表达式,然后利用二如图(２)所示,过点P作PD⊥AC于点D,则有PD∥BC,次函数的极值求得S的最大值;APPDAD１０－２tPDAD(３)要点是利用(２)中求得的△AQP的面积表达式,再∴＝＝,即＝＝．ABBCAC１０６８由线段PQ恰好把△ABC的面积平分,列出一元二次方程;６８解得PD＝６－t,AD＝８－t．由于此一元二次方程的判别式小于０,则可以得出结论:不存５５在这样的某时刻t,使线段PQ恰好把△ABC的面积平分;∴QD＝AD－AQ＝８－８t－２t＝８－１８t．５５(４)首先根据菱形的性质及相似三角形比例线段关系,在Rt△PQD中,由勾股定理得:QD２２２,＋PD＝PQ求得PQ、QD和PD的长度;然后在Rt△PQD中,求得时间２２t的值;最后求菱形的面积,值得注意的是菱形的面积等于即(８－１８t)＋(６－６t)＝(２t)２,５５△AQP面积的２倍,从而可以利用(２)中△AQP面积的表达化简得:１３t２－９０t＋１２５＝０,式,这样可以化简计算．２５【完全解答】∵AB＝１０cm,AC＝８cm,BC＝６cm,解得t１＝５,t２＝．１３∴由勾股定理的逆定理得△ABC为直角三角形,∠C∵０≤t≤４,为直角．２５∴t＝．(１)BP＝２t,则AP＝１０－２t．１３∵PQ∥BC,由(２)可知,S△AQP＝－６t２＋６t．５APAQ∴＝,６ABAC∴S菱形AQPQ′＝２S△AQP＝２×(－t２＋６t)５１０－２t２t２０即＝．解得t＝．６２５２２５１０８９＝２[－５×(１３)＋６×１３]２０∴当t＝９s时,PQ∥BC．２４００(cm２)．＝１６９(２)如图(１)所示,过点P作PD⊥AC于点D．所以存在时刻t,使四边形AQPQ′为菱形,此时菱形的APPD１０－２tPD∴PD∥BC．∴AB＝BC,即１０＝６．２４００２面积为cm．１６９６解得PD＝６－t．【归纳交流】这是一道典型的点运动型问题,解决此类问５题时,一是要搞清在单点运动变化的过程中,哪些图形(如线１S＝×AQ×PD２段、三角形等)随之运动变化,即确定整个单点运动变化过程１６中图形中的变与不变,二是要运用好相应的几何知识,三是＝２×２t×(６－５t)要结合具体问题,建立函数模型,达到解题目的．６(１)＝－t２＋６t【名题选练】５一、选择题２６５１５＝－５(t－２)＋２,１．(２０１２?湖北黄冈)如图,在Rt△ABC中,∠C＝９０°,AC＝５１５２BC＝６cm,点P从点A出发,沿AB方向以每秒２cm的∴当t＝s时,S取得最大值,最大值为cm．２２速度向终点B运动;同时,动点Q从点B出发沿BC方向(３)假设存在某时刻t,使线段PQ恰好把△ABC的面积以每秒１cm的速度向终点C运动,将△PQC沿BC翻折,平分,点P的对应点为点P′．设点Q运动的时间为t秒,若四边则有S１S△ABC,而S△ABC＝１AC×BC＝２４,形QPCP′为菱形,则t的值为()．△AQP＝２２A．２∴此时S△AQP＝１２．B．２６２由(２)可知,S△AQP＝－t＋６t,５C．２２６２２D．３∴－t＋６t＝１２,化简得:t－５t＋１０＝０．５二、解答题２(第１题)∵Δ＝(－５)－４×１×１０＝－１５＜０,此方程无解,２．(２０１２?江苏盐城)如图(１)所示,∴不存在某时刻t,使线段PQ恰好把△ABC的面积已知A、B为直线l上两点,点C为直线l上方一动点,连平分．\n第五章动态问题接AC、BC,分别以AC、BC为边向△ABC外作正方形４．(２０１２?贵州遵义)如图,△ABC是边长为６的等边三角形,CADF和正方形CBEG,过点D作DD１⊥l于点D１,过点P是边AC上一动点,由点A向点C运动(与点A、C不重E作EE１⊥l于点E１．合),Q是CB延长线上一点,与点P同时以相同的速度由(１)如图(２),当点E恰好在直线l上时(此时E１与E重点B向CB延长线方向运动(点Q不与点B重合),过点合),试说明DD１＝AB;P作PE⊥AB于E,连接PQ交AB于点D．(２)在图(１)中,当D、E两点都在直线l的上方时,试探求三(１)当∠BQD＝３０°时,求AP的长;条线段DD１、EE１、AB之间的数量关系,并说明理由;(２)运动过程中线段ED的长是否发生变化?如果不变,(３)如图(３),当点E在直线l的下方时,请直接写出三条求出线段ED的长;如果变化请说明理由．线段DD１、EE１、AB之间的数量关系．(不需要证明)(第４题)(１)(２)(３)５．(２０１２?江苏无锡)如图,菱形ABCD的边长为２cm,∠DAB(第２题)＝６０°．点P从点A出发,以３cm/s的速度沿AC向C作匀速运动;与此同时,点Q也从点A出发,以１cm/s的速度沿射线AB作匀速运动．当P运动到点C时,P、Q都停止运动．设点P运动的时间为ts．(１)当P异于A、C时,请说明PQ∥BC;(２)以P为圆心、PQ长为半径作圆,请问:在整个运动过程中,当t为怎样的值时,☉P与边BC分别有１个公共点和２个公共点?３．(２０１２?湖南常德)已知四边形ABCD是正方形,O为正方形对角线的交点,一动点P从B开始,沿射线BC运动,连接DP,作CN⊥DP于点M,且交直线AB于点N,连接OP、ON．(当P在线段BC上时,如图(１),当P在BC的延长线上时,如图(２))(１)请从图(１)、(２)中任选一图证明下面结论:①BN＝(第５题)CP;②OP＝ON,且OP⊥ON;(２)设AB＝４,BP＝x,试确定以O、P、B、N为顶点的四边形的面积y与x的函数关系．６．(２０１２?江苏苏州)如图,已知半径为２的☉O与直线l相切于点A,点P是直径AB左侧半圆上的动点,过点P作直线l的垂线,垂足为C,PC与☉O交于点D,连接PA、PB,设PC的长为x(２＜x＜４)．５(１)当x＝时,求弦PA、PB的长度;２(２)当x为何值时,PD?CD的值最大?最大值是多少?(１)(２)(第３题)(第６题)\n∴△ADD１≌△CAH(AAS)．∴DD１＝AH．同理:EE１＝BH,∴AB＝AH＋BH＝DD１＋EE１．(３)AB＝DD１－EE１．３．(１)如图(１),∵四边形ABCD是正方形,∴OC＝OB,DC＝BC,∠DCB＝∠CBA＝９０°,∠OCB＝∠OBA＝４５°,∠DOC＝９０°,DC∥AB．∵DP⊥CN,∴∠CMD＝∠DOC＝９０°．∴∠BCN＋∠CPD＝９０°,∠BCN＋∠CNB＝９０°．∴∠CPD＝∠CNB．∵DC∥AB,∴∠DCN＝∠CNB＝∠CPD．∵在△DCP和△CBN中,∠DCB＝∠CBN,∠CPD＝∠BNC,DC＝BC,∴△DCP≌△CBN．∴CP＝BN．∵在△OBN和△OCP中,OB＝OC,∠OCP＝∠OBN,CP＝BN,第五章动态问题∴△OBN≌△OCP．∴ON＝OP,∠BON＝∠COP．§５．１点运动∴∠BON＋∠BOP＝∠COP＋∠BOP,１．B即∠NOP＝∠BOC＝９０°．２．(１)∵四边形CADF、CBEG是正方形,∴ON⊥OP．∴AD＝CA,∠DAC＝∠ABC＝９０°．即ON＝OP,ON⊥OP．∴∠DAD１＋∠CAB＝９０°．(２)∵AB＝４,四边形ABCD是正方形,∵DD１⊥AB,∴点O到边BC的距离是２．∴∠DD１A＝∠ABC＝９０°．图(１)中,y＝S△OBN＋S△OBP,∴∠DAD１＋∠ADD１＝９０°．１１＝×(４－x)×２＋×x×２∴∠ADD１＝∠CAB．２２在△ADD１和△CAB中,＝４(０＜x＜４),∠DD１A＝∠ABC,∠ADD１＝∠CAB,AD＝CA,图(２)中,y＝S△POB＋S△PBN∴△ADD１≌△CAB(AAS)．１１＝×x×２＋×(x－４)×x２２∴DD１＝AB．(２)AB＝DD１＋EE１．＝１x２－x(x＞４),２过点C作CH⊥AB于点H,即以点O、P、B、N为顶点的四边形的面积y与x的函数∵DD１⊥AB,４(０＜x＜４),∴∠DD１A＝∠CHA＝９０°．关系是:y＝１２{x－x(x＞４)．∴∠DAD１＋∠ADD１＝９０°．２∵四边形CADF是正方形,４．(１)∵△ABC是边长为６的等边三角形,∴AD＝CA,∠DAC＝９０°．∴∠ACB＝６０°．∴∠DAD１＋∠CAH＝９０°．∵∠BQD＝３０°,∴∠ADD１＝∠CAH．∴∠QPC＝９０°．在△ADD１和△CAH中,设AP＝x,则PC＝６－x,QB＝x,∠DD１A＝∠CHA,∠ADD１＝∠CAH,AD＝CA,∴QC＝QB＋BC＝６＋x．\n∵在Rt△QCP中,∠BQD＝３０°,∴∠APQ＝∠ACB．１１∴PQ∥BC．∴PC＝QC,即６－x＝(６＋x),解得x＝２．２２(２)如图(２),☉P与BC切于点(２)当点P、Q运动时,线段DE的长度不会改变．M,连接PM,则PM⊥BC．理由:作QF⊥AB,交直线在Rt△CPM中,AB的延长线于点F,连接∵∠PCM＝３０°,QE、PF,１３∵PE⊥AB,∴PM＝２PC＝３－２t．(第５题(２))∴∠DFQ＝∠AEP＝９０°．３由PM＝PQ＝AQ＝t,即３－t＝t,∵点P、Q做匀速运动且速２(第４题)度相同,解得t＝４３－６,此时☉P与边∴AP＝BQ．BC有一个公共点;∵△ABC是等边三角形,如图(３),☉P过点B,此时PQ＝∴∠A＝∠ABC＝∠FBQ＝６０°．PB,在△APE和△BQF中,∵∠PQB＝∠PAQ＋∠APQ(第５题(３))∠A＝∠FBQ,∠AEP＝∠BFQ,＝６０°,∴∠APE＝∠BQF．∴△PQB为等边三角形．∴∠A＝∠FBQ,AP＝BQ,∠AEP＝∠BFQ．∴QB＝PQ＝AQ＝t．∴△APE≌△BQF．∴t＝１．∴AE＝BF,PE＝QF且PE∥QF．∴当４３－６＜t≤１时,☉P与边BC有２个公共点．∴四边形PEQF是平行四边形．如图(４),☉P过点C,此时PC＝PQ,即２３－３t＝t,１∴DE＝２EF．∴t＝３－３．∵EB＋AE＝BE＋BF＝AB,∴当１＜t≤３－３时,☉P与边BC有一个公共点,１当点P运动到点C,即t＝２时,∴DE＝AB．２☉P过点B,此时,☉P与边BC又等边△ABC的边长为６,有一个公共点,∴DE＝３．∴当t＝４３－６或１＜t≤３－∴当点P、Q运动时,线段DE的长度不会改变．３或t＝２时,☉P与菱形ABＧ５．(１)∵四边形ABCD是菱形,且菱形ABCD的边长为CD的边BC有１个公共点;(第５题(４))２cm,当４３－６＜t≤１时,☉P与边BC有２个公共点．１∴AB＝BC＝２,∠BAC＝∠DAB．２６．(１)∵☉O与直线l相切于点A,且AB为☉O的直径,又∠DAB＝６０°,∴AB⊥l．∴∠BAC＝∠BCA＝３０°．又PC⊥l,如图(１),连接BD交AC于点∴AB∥PC．O．∴∠CPA＝∠PAB．∵四边形ABCD是菱形,∵AB是☉O的直径,１∴∠APB＝９０°．∴AC⊥BD,OA＝AC．２又PC⊥l,∴OB＝１AB＝１．(第５题(１))２∴∠PCA＝∠APB＝９０°．∴△PCA∽△APB．∴OA＝３,AC＝２OA＝２３．PCPA运动ts后,AP＝３t,AQ＝t,∴＝．APAB∴AP＝AC＝３．即PA２＝PC×AB．AQAB５又∠PAQ＝∠CAB,∵PC＝,AB＝４,２(第６题)∴△PAQ∽△CAB．\n５∴PA＝×４＝１０．２∴Rt△APB中,AB＝４,PA＝１０．由勾股定理得:PB＝１６－１０＝６．(２)过点O作OE⊥PD,垂足为E．∵PD是☉O的弦,OE⊥PD,∴PE＝ED．又∠CEO＝∠ECA＝∠OAC＝９０°,∴四边形OACE为矩形．∴CE＝OA＝２．又PC＝x,∴PE＝ED＝PC－CE＝x－２．∴CD＝PC－PD＝x－２(x－２)＝x－２x＋４＝４－x．２∴PD?CD＝２(x－２)(４－x)＝－２x＋１２x－１６２＝－２(x－３)＋２．∵２＜x＜４,∴当x＝３时,PD×CD的值最大,最大值是２．