- 2022-09-27 发布 |
- 37.5 KB |
- 54页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
仿生踝关节装置的运动学分析
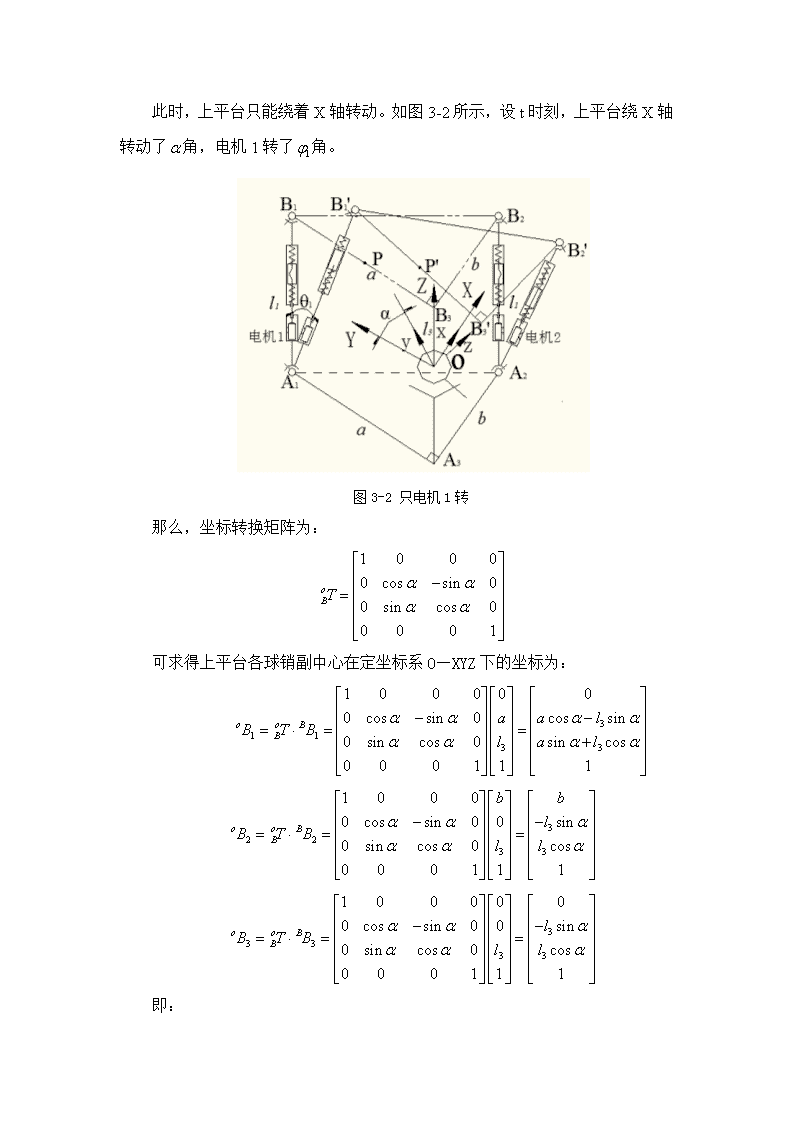
运动学分析3.1位置反解3.1.1建立坐标系如图3-1所示,在大球销副中心O点建立与下平台固定的定坐标系O-XYZ记为,其中X轴平行于,且方向沿方向;Y轴平行于方向沿方向;Z轴平行于,方向沿着方向。再以O点为原点建立与上平台固定的动坐标系O-xyz记为,其中x轴平行于,且方向沿方向;y轴平行于,且方向沿方向;z轴平行于,且方向沿方向。并且,在初始状态下两个坐标系重合。图3-1建立坐标系设初始状态下,,,且,,那么,下平台各球销副中心在定坐标系下\n的坐标为:上平台各球销副中心及上平台重心在动坐标系下的坐标为:3.1.2坐标转换矩阵根据实际机构的模型,上平台只能够绕着O点沿X轴或Y方向转动,不能绕Z轴转动。再加上动、定坐标系原点重合。那么,可将动坐标系看做定坐标系先绕Z轴转角,再绕Y轴转角,最后绕X轴转角后得到的坐标系。那么欧拉角转换矩阵为:3.1.3各种情况下反解方程的建立、求解根据分析,弹簧在压并时整个支链可以看做刚体,而未压并时支链为刚柔组合体。因此应分为两大种情况进行分析。每种情况都要分析只有1个电机动及电机联动的情况,而在刚柔组合分析时还要就上平台有无载荷进行讨论。现设丝杠螺母副的导程为3.1.3.1弹簧压并时当上平台负载较大使弹簧压并时,可以弹簧变形量不再改变,可将弹簧当做刚体。这时含弹簧的支链都可当做刚体来计算。(1)只启动电机1,不启动电机2时\n此时,上平台只能绕着X轴转动。如图3-2所示,设t时刻,上平台绕X轴转动了角,电机1转了角。图3-2只电机1转那么,坐标转换矩阵为:可求得上平台各球销副中心在定坐标系O—XYZ下的坐标为:即:\n则:杆长度变化量为:又因为在压并状态下所以:(3.1)解(3.1)式得:(3.2)(2)只启动电机1,不启动电机2时此时,上平台只能绕着Y轴转动。如图3-3所示,设t时刻,上平台绕Y轴转动了角,电机1转了角。图3-3只电机2启动那么,坐标转换矩阵为:\n可求得上平台各球销副中心在定坐标系O—XYZ下的坐标为:即:则:杆长度变化量为:又因为在压并状态下所以:(3.3)解(3.3)式得:(3.4)(3)两个电机联动时\n设t时刻上平台的欧拉角为,电机1转了角,电机2转了角。此时的转换矩阵为:可求得上平台各球销副中心在定坐标系O—XYZ下的坐标为:即:则:杆长度变化量为:\n(3.5)又因为在压并状态下所以:(3.6)杆长度变化量为:又因为在压并状态下所以:(3.7)解(3.6)、(3.7)式得:(3.8)(3.9)3.1.3.2弹簧未压并时此时,弹簧的压缩量能发生改变,不能将弹簧看做刚体,丝杠螺母副带动螺母走的距离等于弹簧压缩量的改变量与含弹簧支链长度变化量的和。设四个弹簧的弹性系数为,下面分情况进行计算(1)只有电机1启动,电机2不启动\n①无载时先在初始状态下求出支链1上下弹簧初始压缩量、以及支链2上下弹簧初始压缩量、如图3-4所示,初始状态下对上平台受力分析图3-4上平台受力分析图按实际的模型,上平台的重量沿着对称分布,上平台的重心P点在的中心。那么支链2对上平台是辅助支撑,故,支链1对上平台的支撑力、支链3对上平台的支撑力沿着Z轴正方向,上平台的重力G沿Z轴负方向。对上平台列平衡方程:(3.10)(3.11)其中,由(3.10)、(3.11)式解得:再分别对支链1、2的移动箱受力分析,如图3-5、3-6所示\n图3-5支链1移动箱图3-6支链2移动箱设移动箱的质量为,重力为对1支链移动箱列平衡方程:(3.12)其中:带入(3.12)式解得:当给定后,也就确定。再对2支链的移动箱列平衡方程:(3.13)其中:带入(3.13)式解得:当给定后,也就确定。当电机1转动后,设t时刻上平台绕着X轴转动了角,电机1的转角为如图3-7,先将支链1分为3部分:\n图3.7支链1如图3-8,对支链1各部件受力分析:abc图3-8支链1各部件受力分析如图3-8a是对3(二力杆)受力分析;图3-8b是对4(螺母)受力分析;图3-8c是对5(移动箱)受力分析。再对支链2受力分析:由于上平台转动后支链2长度变长而电机2并未转动使得支链2的弹簧变成了拉簧。如图3-9,对支链2的二力杆与移动箱的整体受力分析:\n图3-9支链2的二力杆与移动箱的整体受力分析对支链3受力分析:如图3-10,二力杆受力:图3-10对支链3受力分析最后,对转动后的上平台受力分析,如图3-11所示:图3-11对上平台受力分析\n显然:其中沿方向,沿反方向,沿方向,作用于P点沿着Z轴反方向。上平台质心P点在定坐标系下的坐标为:那么,点在三个坐标轴上的加速度为:那么由平衡条件:,列出方程:对,X轴方向:Y轴方向:(3.13)Z轴方向:(3.14)对有:(3.15)由(3.13)、(3.14)、(3.15)解得:\n(3.16)其中:再沿方向看支链1:设在方向上螺母上升了,移动箱上升了,那么弹簧压缩量的该变量为:那么:对移动箱列微分方程:\n(3.17)再根据初始条件:解(3.17)式可得:(3.18)其中,由于螺母由丝杠带动上升,故带入(3.18)式得到:(3.19)又因为也等于支链1长度的增加量,故:(3.20)联立(3.19)(3.20)式得:(3.21)解(3.21)式得:(3.22)其中:,②有载时当上平台有载时,支链1所受压力变大,这会使支链1的弹簧压缩量增加,使得整个1支链长度减小,上平台会倾斜。此时应启动电机1\n使得螺母上升一段距离使得支链1与支链2长度重新相等。让初始状态时上平台呈水平状态。对初始时上平台受力分析,如图3-12所示,求出有载时四个弹簧的初始压缩量、、、图3-12上平台受力分析考虑到上平台的重量、所加的载荷都是沿着对称分布。所以支链2仍是辅助支撑,故对上平台列平衡方程:(3.23)(3.24)解(3.23)(3.24)得:再分别对支链1、2的移动箱受力分析,如图3-13、3-14所示\n图3-13支链1移动箱图3-14支链移动箱设移动箱的质量为,重力为对1支链移动箱列平衡方程:(3.25)其中:再结合,全部带入(3.25)式解得:再对2支链的移动箱列平衡方程:(3.26)其中:,再结合可以确定当电机1转动后,设t时刻上平台绕着X轴转动了角,电机1的转角为\n如图3-15,先将支链1分为3部分:图3-15支链1如图3-16,对支链1各部件受力分析:abc图3-16支链1各部件受力分析\n图3-16a对3(二力杆)受力分析;图3-16b对4(螺母)受力分析;图3-16c对5(移动箱)受力分析再对支链2受力分析,由于上平台转动后支链2长度变长而电机2并未转动使得支链2的弹簧变成了拉簧。如图3-17,对支链2的二力杆与移动箱的整体受力分析:图3-17支链2二力杆与移动箱整体受力分析对支链3受力分析:如图3-18,二力杆受力:图3-18最后,对转动后的上平台受力分析,如图3-19所示:\n图3-19对上平台受力分析显然:其中沿方向,沿反方向,沿方向,作用于P点沿着Z轴反方向,作用于P点方向垂直于上平台向下。现求出的方向向量:设是的方向向量,由于垂直于上平台,可得到:(3.27)(3.28)由(3.27)(3.28)式解得:,故:上平台质心P点在定坐标系下的坐标为:那么,点在三个坐标轴上的加速度为:\n那么由平衡条件:,列出方程:对,X轴方向:Y轴方向:(3.29)Z轴方向:(3.30)对有:(3.31)由(3.28)、(3.29)、(3.30)解得:(3.32)其中:其余的系数与无载时的一致。再沿方向看支链1:设在方向上螺母上升了,移动箱上升了,那么弹簧压缩量的该变量为:那么:\n对移动箱列微分方程:(3.33)再根据初始条件:解(3.33)式可得:(3.34)其中,由于螺母由丝杠带动上升,故带入(3.34)式得到:(3.35)又因为也等于支链1长度的增加量,故:(3.36)联立(3.35)(3.36)式得:(3.37)解(3.37)式得:(3.38)\n其中:,(2)只有电机2启动,电机1不启动①无载时先在初始状态下求出支链1上下弹簧以及支链2上下弹簧初始压缩量:初始状态下对上平台受力分析,受力情况与图3-4完全一致,故四个弹簧的初始压缩量分别为:,,,当电机2转动后,设t时刻上平台绕着Y轴转动了角,电机2的转角为,然后对支链1、支链2、支链3、上平台分别受力分析:如图3-20,将支链2分为3部分:图3-20支链2如图3-21,对支链2各部件受力分析:\nabc图3-21支链2各部件受力分析图3-21a对3(二力杆)受力分析;图3-21b对4(螺母)受力分析;图3-21c对5(移动箱)受力分析。再对支链1受力分析:由于上平台转动后支链1长度变长而电机1并未转动使得支链1的弹簧变成了拉簧。如图3-22,对支链1的二力杆与移动箱的整体受力分析:图3-22支链1的二力杆与移动箱的整体受力分析对支链3受力分析:如图3-23,二力杆受力:图3-23支链3受力分析\n最后,对转动后的上平台受力分析,如图3-24所示:图3-24上平台受力分析显然:其中沿反方向,沿方向,沿方向,作用于P点沿着Z轴反方向。上平台质心P点在定坐标系下的坐标为:那么,点在三个坐标轴上的加速度为:那么由平衡条件:,列出方程:\n对,X轴方向:(3.39)Y轴方向:Z轴方向:(3.40)对有:(3.41)由(3.39)、(3.40)、(3.41)解得:(3.42)其中:\n再沿方向看支链2:设在方向上螺母上升了,移动箱上升了,那么弹簧压缩量的该变量为:那么:对移动箱列微分方程:(3.43)其中,再根据初始条件:解(3.43)式可得:(3.44)其中,由于螺母由丝杠带动上升,故带入(3.44)式得到:(3.45)又因为也等于支链1长度的增加量,故:(3.46)\n联立(3.45)(3.46)式得:(3.47)解(3.47)式得:(3.48)其中:②有载时当上平台有载时,支链1所受压力变大,这会使支链1的弹簧压缩量增加,使得整个1支链长度减小,上平台会倾斜。此时应启动电机1使得螺母上升一段距离使得支链1与支链2长度重新相等。让初始状态时上平台呈水平状态。初始状态下对上平台受力分析,受力情况与图3-12完全一致,故四个弹簧的初始压缩量分别为:,,,当电机2转动后,设t时刻上平台绕着Y轴转动了角,电机2的转角为,然后对支链1、支链2、支链3、上平台分别受力分析:如图3-25,将支链2分为3部分图3-25支链2\n如图3-26,对支链2各部件受力分析:abc图3-26支链2各部件受力分析图3-26a对3(二力杆)受力分析;图3-26b对4(螺母)受力分析;图3-26c对5(移动箱)受力分析。再对支链1受力分析:由于上平台转动后支链1长度变长而电机1并未转动使得支链1的弹簧变成了拉簧。如图3-27,对支链1的二力杆与移动箱的整体受力分析:图3-27支链1的二力杆与移动箱的整体受力分析对支链3受力分析:如图3-28,二力杆受力:\n图3-28支链3受力分析最后,对转动后的上平台受力分析,如图3-29所示:图3-29上平台受力分析显然:其中沿反方向,沿方向,沿方向,作用于P点沿着Z轴反方向,作用于P点方向垂直于上平台向下。现求出的方向向量:设是的方向向量,由于垂直于上平台,可得到:(3.49)(3.50)由(3.49)(3.50)式解得:,故:\n上平台质心P点在定坐标系下的坐标为:那么,点在三个坐标轴上的加速度为:那么由平衡条件:,列出方程:对,X轴方向:(3.51)Y轴方向:Z轴方向:(3.52)对有:(3.53)由(3.51)、(3.52)、(3.53)解得:(3.54)其中:\n其余的系数与无载时的一致。再沿方向看支链2:设在方向上螺母上升了,移动箱上升了,那么弹簧压缩量的该变量为:那么:对移动箱列微分方程:(3.55)其中,再根据初始条件:解(3.55)式可得:(3.56)其中,由于螺母由丝杠带动上升,故带入(3.56)式得到:(3.57)又因为也等于支链1长度的增加量,故:(3.58)\n联立(3.57)(3.58)式得:(3.59)解(3.59)式得:(3.60)其中:(3)两电机联动时:①无载时:先在初始状态下求出支链1上下弹簧以及支链2上下弹簧初始压缩量:初始状态下对上平台受力分析,受力情况与图3-4完全一致,故四个弹簧的初始压缩量分别为:,,,设t时刻,上平台先绕Y轴转了角,在绕X轴转了角,电机1的转角为,电机2的转角为。对各支链及上平台受力分析:先对支链1受力分析:同样地,将支链1分为三部分,如图3-30所示:\n图3-30支链1分别对各部件受力分析如图3-31所示:abc图3-31支链1各部件受力分析图3-31a对3(二力杆)受力分析;图3-31b对4(螺母)受力分析;图3-31c对5(移动箱)受力分析。再对支链2受力分析:与支链1相同,分成三部分。分别对各部件受力分析如图3-32所示:\nabc图3-32支链2各部件受力分析图3-32a对3(二力杆)受力分析;图3-32b对4(螺母)受力分析;图3-32c对5(移动箱)受力分析。然后后对支链3受力分析,如图3-33所示:\n图3-33支链3受力分析最后对上平台受力分析,如图3-34所示:图3-34上平台受力分析显然:,,其中,沿方向,沿方向,沿方向,沿Z轴负方向。上平台质心P点在定坐标系下的坐标为:\n那么,点在三个坐标轴上的加速度为:由平衡条件:X方向:(3.61)Y方向:(3.62)Z方向:\n(3.63)解(3.62)(3.62)(3.63)得:(3.64)(3.65)其中:\n沿方向看支链1:设在方向上螺母上升了,移动箱上升了,弹簧压缩量的改变量为:由于丝杠螺母副带动螺母,则:则:对移动箱列微分方程:,且即(3.66)解(3.66)式得的通解为:其中,由t=0时,且,得出:,得到\n(3.67)再将,代入(3.67)式得:(3.68)又由于也等于支链1长度变化量,故(3.69)联立(3.68)(3.69)式解出:(3.70)其中,再沿着沿方向看支链2:设在方向上螺母上升了,移动箱上升了,弹簧压缩量的改变量为:由于丝杠螺母副带动螺母,则:则:对移动箱列微分方程:,且即:(3.71)解(3.71)式得的通解为:\n其中,由t=0时,且,得出:,得到:(3.72)再将,代入(3.72)式得:(3.73)又由于也等于支链2长度变化量,故(3.74)联立(3.73)(3.74)式解出:(3.75)②有载时先在初始条件下,求出各弹簧的初始压缩量:此时的上平台、各支链的受力情况与图3-12完全一致,故四个弹簧初始压缩量为:,,,设t时刻,上平台先绕Y轴转了角,在绕x轴转了角,电机1的转角为,电机2的转角为。\n对各支链及上平台受力分析:与前面无载时分析方法一样,支链1、2都分成三部分。先对支链1各部分受力分析,如图3.35所示:abc图3-35支链1各部分受力分析图3-35a对3(二力杆)受力分析;图3-35b对4(螺母)受力分析;图3-35c对5(移动箱)受力分析。再对支链2各部分受力分析,如图3-36所示:abc图3-36支链2各部分受力分析图3-36a对3(二力杆)受力分析;图3-36b对4(螺母)受力分析;图3-36c对5(移动箱)受力分析。\n然后对支链3受力分析,如图3-37所示:图3-37支链3受力分析最后对上平台受力分析,如图3-38所示:图3-38上平台受力分析其中,沿方向,沿方向,沿方向,沿z轴负方向,作用于P点且垂直于上平台方向向下。上平台质心坐标及三个坐标轴上的加速度与无载时的一样。现确定出的方向:设的一个方向向量为。那么:垂直于上平台,故:\n解得:,故:由平衡条件:X方向:(3.76)Y方向:(3.77)Z方向:(3.78)其中:其余参数与无载时一样解(3.76)(3.77)(3.78)得:(3.79)(3.80)其中:其余参数与无载时一样。沿方向看支链1:设在方向上螺母上升了,移动箱上升了,弹簧压缩量的改变量为:\n由于丝杠螺母副带动螺母,则:则:对移动箱列微分方程:,且即(3.81)解(3.81)式得的通解为:其中,由t=0时,且,得出:,得到:(3.82)再将,代入(3.82)式得:(3.83)又由于也等于支链1长度变化量,故(3.84)联立(3.83)(3.84)式解出:\n(3.85)其中,再沿着沿方向看支链2:设在方向上螺母上升了,移动箱上升了,弹簧压缩量的改变量为:由于丝杠螺母副带动螺母,则:则:对移动箱列微分方程:,且即(3.86)解(3.86)式得的通解为:其中,由t=0时,且,得出:,得到:(3.87)再将,代入(3.87)式得:\n(3.88)又由于也等于支链2长度变化量,故(3.89)联立(3.88)(3.89)式解出:(3.90)3.2位置正解与求反解时相同,分情况求解3.2.1弹簧压并情况下3.2.1.1只启动电机1,不启动电机2时与求解反解时方法相同,在得到(3.1)式后,先进行化简得到:(3.91)解(3.91)式求出:(3.92)3.2.1.2只启动电机2,不启动电机1时与求解反解时方法相同,在得到(3.3)式后,先进行化简得到:\n(3.93)解(3.93)式得:(3.94)3.2.1.3两个电机联动时与求解反解时方法相同,在得到(3.6)、(3.7)式后,分别进行化简得到:(3.95)(3.96)联立(3.95)、(3.96)可解出与3.2.2弹簧未压并时由于未压并时位置求解公式比较复杂,且本机构是并联机构,其位置正解若使用解析法求解虽能得到全部解,但计算速度很慢。同时,考虑到运动的连续性,得到的全部解中有一部分在机构实际运动中不会达到。又由于并联机构的反解已在前面全部求出,故使用数值法求解位置正解较为简単。其基本原理是利用以上求得的机构反解逐步迭代完成,求出一组解。这种数值求法快捷简便,而且求得的解一定能在机构运动中达到。位置正解是已知两电机的转角求出动平台的位姿。假定动平台的初始姿态是\n(,,),(以上平台水平状态下为上平台的初始位姿,即,,),由上面的反解公式可求出初始位姿下电机转角为:,。当已知电机转角为时,则两者之差为:(3.97)由(3.97)式知是动平台位姿变量的函数,即:,考虑到上平台不能绕Z轴转动,角始终为0,故:(i=1,2)(3.98)因此,2个电机转角与上平台转动角速度有如下关系:(3.99)(3.99)式中:,分别为2个电机的转动角速度;,分别表示上平台姿态角的变化速度,将上式两边同乘以,并用表示点检转角的增量,上平台的姿态增量用()表示,可得:(3.100)式(3.100)中右上标表示第一次修正,因此由就可以求得第一次姿态修正增量(),即可得到第一次修正后的动平台姿态分量:\n再由得到的修正后的姿态(,,)通过位置反解方程求出新的电机转角。显然,向有所逼近。也可得到第二次电机转角偏差,再把带入式(3.100)中,可得(),即第二次姿态修正量,也就得到了第二次修正后的平台姿态分量:由位置反解方程可求得在此姿态下的新电机转角向进一步逼近,重复以上各个过程,在连续不断的平台姿态修正后,会得到一系列逐次逼近给定电机转角的新转角,当得到的新转角与已知给定的转角的最大偏差小于允许偏差时,则终止上述反解迭代过程,而此时与心得电机转角对应的动平台姿态(,,0)就可以认为是所要求解的实际位姿。当然,使用这种方法只能求出一组解。但考虑到机构实际运动过程中的连续性,该解一定是运动过程中的可行解。3.3机构的雅可比矩阵分析3.3.1定义雅可比矩阵对于本机构而言,上平台的两个欧拉角,为输出量,两个电机的转角,为输入量。那么就有:(3.101)\n式中的即为机构的雅可比矩阵。同样也可以定义:(3.102)式中的即为机构的雅可比逆矩阵。3.3.2求解雅可比矩阵按照求解位置时的分类方法将求得的位置方程对时间t进行求导得到雅克比矩阵。考虑到并联机构的位置反解表达式较简单,故先求出雅可比逆矩阵。将雅可比逆矩阵写成:(3.103)3.3.2.1弹簧压并时(1)只电机1转将(3.2)式两边对时间t进行求导,可求得:(2)只电机2转时将(3.4)式两边对时间t进行求导,可求得:\n(3)联动时将(3.8)、(3.9)两边对时间t进行求导,可求得:3.3.2.2弹簧未压并时(1)只电机1启动将(3.37)式对时间t进行求导,求得电机1转动角速度为:\n(3.104)且这种情况下其中:其余参数与求解弹簧未压并且上平台有载、只电机1启动时的位置反解的参数一样。当上平台无载时,将所有参数中所含的为0即可。(2)只电机2启动将(3.60)式对时间t进行求导,求得电机1转动角速度为:(3.105)且这种情况下其中:\n其余参数与求解弹簧未压并且上平台有载、只电机2启动时的位置反解的参数一样。当上平台无载时,将所有参数中所含的为0即可。(3)两电机联动时:分别将(3.70)、(3.75)式两边对时间t进行求导,可分别求出两电机的转动角速度:(3.106)(3.107)其中:\n其余参数与求解弹簧未压并且上平台有载、电机联动时的位置反解的参数一样。当上平台无载时,将所有参数中所含的为0即可。在求得雅可比逆矩阵的表达式后,只要将具体的机构参数和位姿参数代入,然后再求逆,就可以得到雅可比矩阵的具体数值,从而得到电机转动角速度与上平台转动角速度的传递关系。查看更多