- 2022-09-27 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
云台中学2011年第一轮复习教案:第30课时图形运动专题(四边形类)
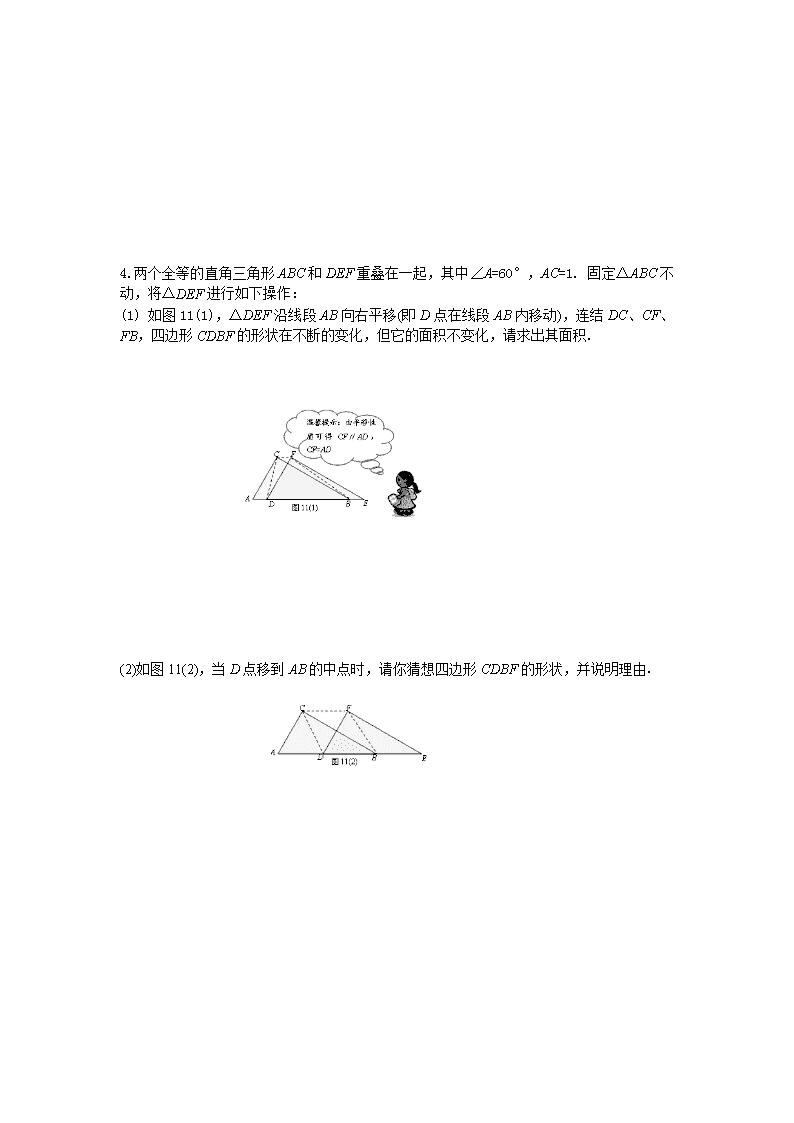
第30课时图形运动专题(四边形类)【课标要求】动点题是近年来中考的的一个热点问题,解这类题目要“以静制动”,即把动态问题,变为静态问题来解。一般方法是抓住变化中的“不变量”,以不变应万变,首先根据题意理清题目中两个变量X、Y的变化情况并找出相关常量,第二,按照图形中的几何性质及相互关系,找出一个基本关系式,把相关的量用一个自变量的表达式表达出来,然后再根据题目的要求,依据几何、代数知识解出。第三,确定自变量的取值范围,画出相应的图象。【知识要点】动态几何问题是近年来中考数学试题的热点题型之一,常以压轴题型出现。这类问题主要是集中代数、几何、三角、函数知识于一体,综合性较强。常用到的解题工具有方程的有关理论,三角函数的知识和几何的有关定理。本节主要说明与四边形有关的运动问题。【典型例题】【例1】如图:□ABCD的对角线AC、BD相交于点O,BD=12cm,AC=6cm,点E在线段BO上从点B以1cm/s的速度运动,点F在线段OD上从点O以2cm/s的速度运动.⑴若点E、F同时运动,设运动时间为t秒,当t为何值时,四边形AECF是平行四边形.⑵在⑴的条件下,①当AB为何值时,四边形AECF是菱形;②四边形AECF可以是矩形吗?为什么?【例2】如图,矩形ABCD中,AB=4cm,BC=8cm,动点M从点D出发,按折线DCBAD方向以2cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1cm/s的速度运动.(1)若动点M、N同时出发,经过几秒钟两点相遇?(2)若点E在线段BC上,且BE=3cm,若动点M、N同时出发,相遇时停止运动,经过几秒钟,点A、E、M、N组成平行四边形?\n【课堂检测】1.如图所示,把菱形ABCD沿着对角线AC的方向移动到菱形A′B′C′D′的位置,它们的重叠部分(图中阴影部分)的面积是菱形ABCD的面积的,若AC=,则菱形移动的距离AA′是()A.B.C.1D.-12.(本题共10分)如图,E是矩形ABCD边BC的中点,P是AD边上一动点,PF⊥AE,PH⊥DE,垂足分别为F,H.(1)当矩形ABCD的长与宽满足什么条件时,四边形PHEF是矩形?请予以证明.(2)在(1)中,动点P运动到什么位置时,矩形PHEF变为正方形?为什么?ABCDEPFH3.如图,在矩形中,,点从点沿边向点以的速度移动;同时,点从点沿边向点以的速度移动。问:⑴几秒钟后的面积等于?⑵几秒钟后⊥?⑶是否存在这样的时刻,使,试说明理由?\n4.两个全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC=1.固定△ABC不动,将△DEF进行如下操作:(1)如图11(1),△DEF沿线段AB向右平移(即D点在线段AB内移动),连结DC、CF、FB,四边形CDBF的形状在不断的变化,但它的面积不变化,请求出其面积.(2)如图11(2),当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明理由.\n【课后作业】5.如图,在等腰梯形ABCD中,AD∥BC,AB=DC=5,AD=6,BC=12,动点P从D点出发沿DC以每秒1个单位的速度向终点C运动,动点Q从C点出发沿CB以每秒2个单位的速度向B点运动。两点同时出发,当P点到达C点时,Q点随之停止运动。(1)梯形ABCD的面积等于;(2)当PQ∥AB时,P点离开D点的时间等于;(3)当P、Q、C三点构成直角三角形时,P点离开D点多少时间?6.(本题满分8分)如图,在△ABC中,∠C=90°,AC=8,BC=6.P是AB边上的一个动点(异于A、B两点),过点P分别作AC、BC边的垂线,垂足为M、N.设AP=x.(1)在△ABC中,AB=▲;(2)当x=▲时,矩形PMCN的周长是14;(3)是否存在x的值,使得△PAM的面积、△PBN的面积与矩形PMC\nN的面积同时相等?请说出你的判断,并加以说明.7.如图9,中,点P是边上的一个动点,过P作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.(1)求证:PE=PF;(2)当点P在边上运动时,四边形BCFE可能是菱形吗?说明理由;(3)若在AC边上存在点P,使四边形AECF是正方形,且.求此时∠A的大小.\n8.(2010·汕头)如图(1),(2)所示,矩形ABCD的边长AB=6,BC=4,点F在DC上,DF=2.动点M、N分别从点D、B同时出发,沿射线DA、线段BA向点A的方向运动(点M可运动到DA的延长线上),当动点N运动到点A时,M、N两点同时停止运动.连接FM、FN,当F、N、M不在同一直线时,可得△FMN,过△FMN三边的中点作△PWQ.设动点M、N的速度都是1个单位/秒,M、N运动的时间为x秒.试解答下列问题:(1)说明△FMN∽△QWP;(2)设0≤x≤4(即M从D到A运动的时间段).试问x为何值时,△PWQ为直角三角形?当x在何范围时,△PQW不为直角三角形?(3)问当x为何值时,线段MN最短?求此时MN的值.\n查看更多