- 2022-09-27 发布 |
- 37.5 KB |
- 11页

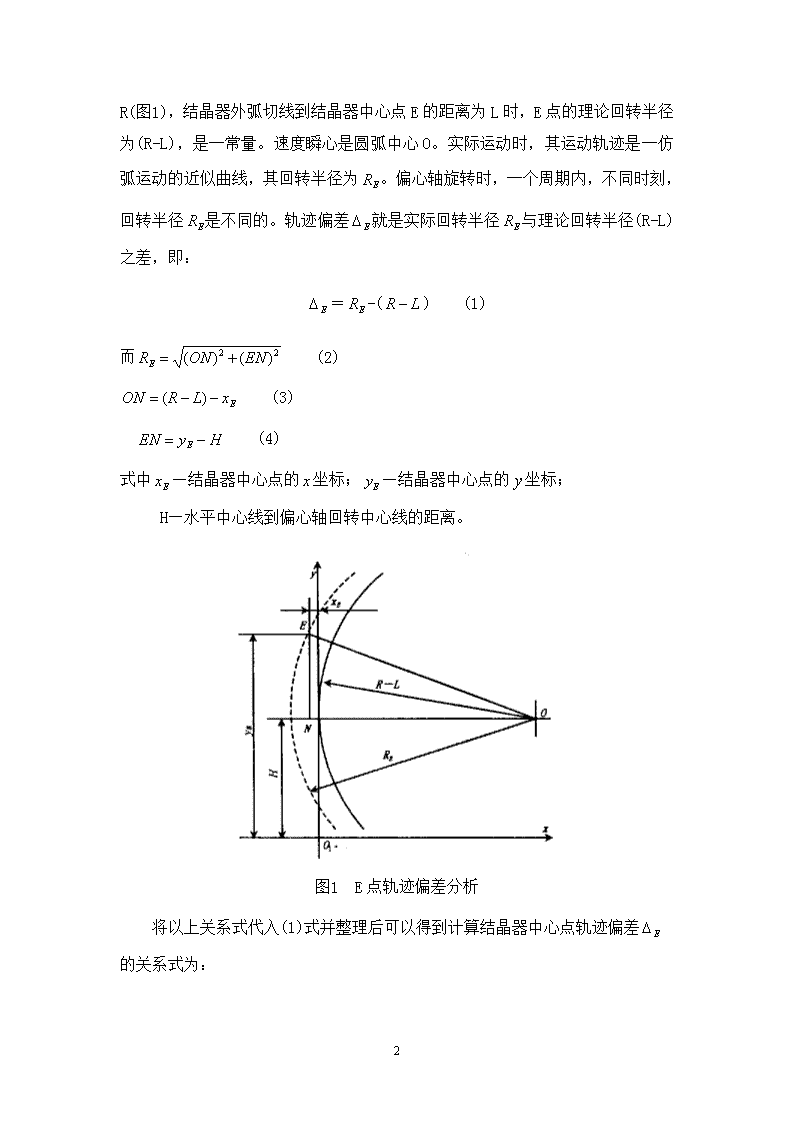
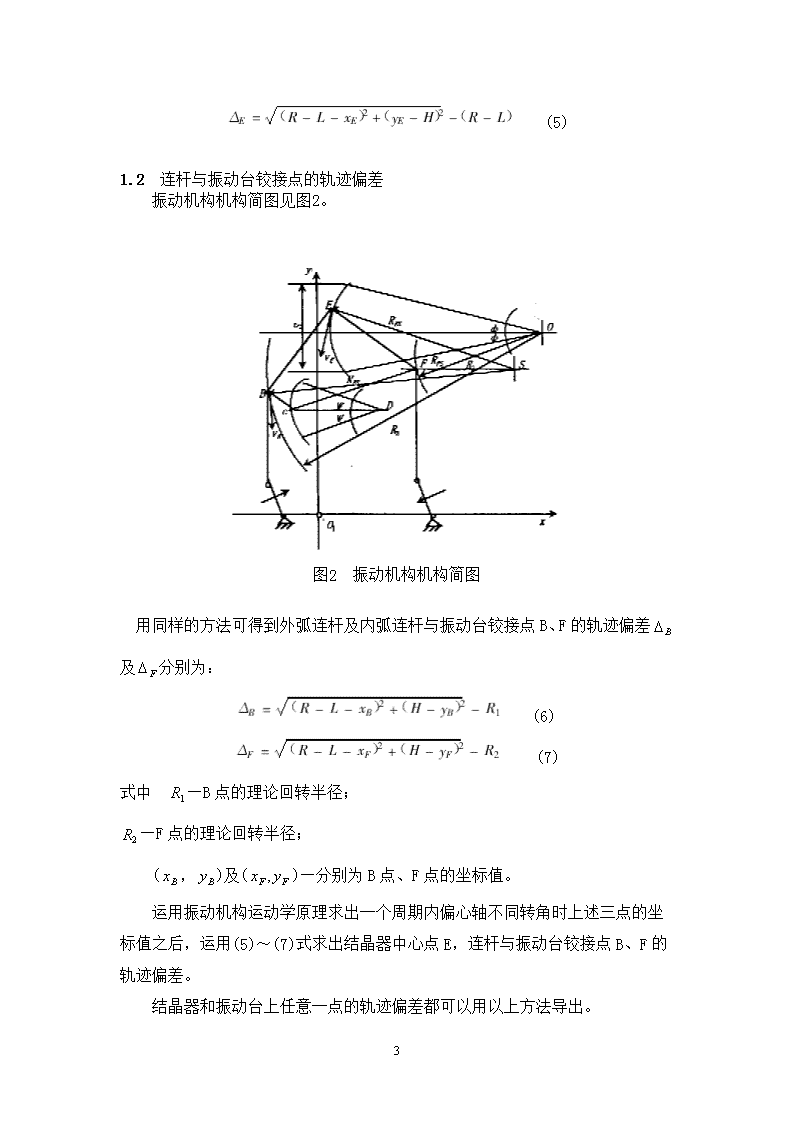
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
连铸结晶器振动机构运动误差分析
连铸结晶器振动机构运动误差分析(内蒙古科技大学孟凡超)摘 要:介绍了连铸结晶器振动机构运动误差产生的原因、影响因素,振动机构运动误差分析方法以及机构设计、调整中应注意的问题。关键词:连铸;结晶器;振动机构;轨迹偏差;瞬心偏差ANALYSISOFMOVEMENTERROROFMOLDOSCILLATINGMECHANISMFORCONTINUOUSCASTINGAbstract:Thecausesofmovementerrorformedbymoldoscillatingmechanismforcontinuouscastinganderrorinfluencingfactorsweredescribed.Theanalyticalmethodofmovementerroroftheoscillatingmechanismandthedesignandadjustmentofthemechanismwereintroduced.KeyWords:Continuouscasting;mold;oscillatingmechanism;locusdeviation;instantanouscenterdeviation 振动机构运动误差包括轨迹偏差和瞬心偏差,振动机构运动时,振动台及结晶器上各点实际上是作仿弧运动,其实际轨迹与理论轨迹有偏差。振动机构运动时,振动台及结晶器上各点的运动速度是变化的,其速度瞬心的位置也是变化的,与理论的运动中心不重合,这就是瞬心偏差。结晶器各点,特别是结晶器中心点的运动误差会影响铸坯质量,过大的偏差还会导致拉漏事故发生。因此,控制各点特别是结晶器中心点运动误差是非常重要的,而且运动误差分析还是机构进行优化设计时选取目标函数的依据。1 结晶器各点的轨迹偏差分析1.110\n 结晶器中心点的轨迹偏差分析 从原理上讲,结晶器振动时,其中心点E作圆弧运动,当铸机圆弧半径为R(图1),结晶器外弧切线到结晶器中心点E的距离为L时,E点的理论回转半径为(R-L),是一常量。速度瞬心是圆弧中心O。实际运动时,其运动轨迹是一仿弧运动的近似曲线,其回转半径为。偏心轴旋转时,一个周期内,不同时刻,回转半径是不同的。轨迹偏差就是实际回转半径与理论回转半径(R-L)之差,即:=-() (1)而 (2) (3) (4)式中—结晶器中心点的坐标;—结晶器中心点的坐标; H—水平中心线到偏心轴回转中心线的距离。图1 E点轨迹偏差分析 将以上关系式代入(1)式并整理后可以得到计算结晶器中心点轨迹偏差的关系式为:10\n (5)1.2 连杆与振动台铰接点的轨迹偏差 振动机构机构简图见图2。 图2 振动机构机构简图 用同样的方法可得到外弧连杆及内弧连杆与振动台铰接点B、F的轨迹偏差及分别为: (6) (7)式中 —B点的理论回转半径;—F点的理论回转半径; (,)及()—分别为B点、F点的坐标值。 运用振动机构运动学原理求出一个周期内偏心轴不同转角时上述三点的坐标值之后,运用(5)~(7)式求出结晶器中心点E,连杆与振动台铰接点B、F的轨迹偏差。 结晶器和振动台上任意一点的轨迹偏差都可以用以上方法导出。10\n1.3 纵向导向板弹簧对运动轨迹偏差的影响 纵向导向板弹簧与振动台的联结点C(参见图2),C点也作仿弧运动,C点的轨迹偏差为: (8)式中 —导向板弹簧的长度; —振动台摆动角度; —为导向板弹簧摆角; —C点振动的理论半径。 C点的轨迹偏差与结晶器中心点的轨迹偏差可由它们之间的几何关系导出,即: (9) 将(8)式进行变换,并分别对及φ求偏导数得: (10) (11) 由振动机构的几何结构可知,恒小于0,对于为单减函数,即随着导向板弹簧长度的增加,C点的轨迹偏差将减小,由(9)式可知E点仿弧运动精度提高。 同理,因为恒大于0,对于φ为单增函数,也就是说,当振动行程增大时,摆动角φ增大,轨迹偏差增大,E点的仿弧运动精度降低。 根据以上分析可以得出设计纵向导向板弹簧的原则是: (1)为提高振动机构运动精度,减少仿弧运动的轨迹偏差(或),应尽量增加纵向导向板弹簧的长度10\n。 (2)确定了振动机构结晶器中心点E的轨迹偏差后,运用(9)式求出C点的轨迹偏差,依此值确定板弹簧的长度。 (3)当要求的轨迹偏差一定时,振动机构取不同的振幅值,求得弹簧长度,也不相同,设计时,取最大振幅进行计算,实际使用的板弹簧长度必须大于计算得到的值。2 振动机构运动时的瞬心偏差分析 振动机构作仿弧运动时,一个周期内各点速度是变化的,其速度瞬心是变化的,并不都与连铸机圆弧中心重合,具有一定的误差,这就是速度瞬心偏差。 偏心轴处于任一转角时的速度瞬心偏差如图2所示。 设外弧连杆与振动台铰接点B的速度为,振动台的转动角速度为,任一时刻B点的回转半径为,⊥,则有如下关系式: (12) 结晶器中心点E的速度为,振动台回转角速度仍为(同一构件其角速度相同)。E点运动时,其回转半径为,⊥,有如下关系式: (13) 半径及半径的交点S即为某瞬时的速度瞬心,其坐标为(),可运用Ⅲ级杆组的分析方法来求出该点的坐标值()[1],根据上述分析方法即可求出偏心轴处于某一转角时的瞬心偏差: 方向的瞬心偏差是:=(14)方向的瞬心偏差是:=- (15) 速度瞬心偏差为:10\n (16) 将结晶器一个运动周期内的瞬心坐标()的值依次代入(16)式,可求出各时刻的瞬心偏差S。3 各种工况下运动轨迹偏差及瞬心偏差计算及分析 运用以上所分析的各关系式,可对振动机构偏心轴转一转时的轨迹偏差及瞬心偏差进行计算。 表1~3是攀钢连铸机原振动机构六种工况的轨迹偏差和瞬心偏差,计算时,偏心轴转角每变化1°计算一次,一个周期内,每种工况得到360组值,但限于篇幅,这里只列出了偏心轴每变化20°的值。每种工况有18个点。表1 振幅±3mm转速100r/min时的轨迹偏差和瞬心偏差α/(°)轨迹偏差mm瞬心偏差mmα/(°)轨迹偏差/mm瞬心偏差/mm96.59-0.0170.016-83.41-0.0180.01776.59-0.014145.990-103.41-0.014154.88356.59-0.011124.370-123.41-0.008123.58236.59-0.00380.082-143.41-0.00380.30816.590.00227.489-163.410.00228.486-3.410.00229.618-183.410.00228.135-23.41-0.00381.646-203.41-0.00378.008-43.41-0.010124.309-223.41-0.010120.477-63.41-0.014150.721-243.41-0.016150.025最大轨迹偏差为-0.018mm,出现在α=-83.41°;最大瞬心偏差为158.682mm,出现在α=100.41°处。表2 振幅±3mm转速180r/min时的轨迹偏差和瞬心偏差10\nα/(°)轨迹偏差mm瞬心偏差mmα/(°)轨迹偏差/mm瞬心偏差/mm96.59-0.0170.016-83.41-0.0180.01776.59-0.014145.819-103.41-0.014154.60756.59-0.011124.665-123.41-0.008123.38236.59-0.00380.082-143.41-0.00380.84216.590.00225.867-163.410.00228.269-3.410.00229.410-183.410.00228.568-23.41-0.00382.097-203.41-0.00378.326-43.41-0.010124.557-223.41-0.010120.477-63.41-0.014150.764-243.41-0.016149.618最大轨迹偏差为-0.018mm,出现在α=-83.41°;最大瞬心偏差为167.162mm,出现在α=-93.41°处。表3 振幅±7.5mm转速180r/min时的轨迹偏差和瞬心偏差α/(°)轨迹偏差mm瞬心偏差mmα/(°)轨迹偏差/mm瞬心偏差/mm96.59-0.0160.017-83.41-0.0160.01776.59-0.013275.782-103.41-0.013307.45256.59-0.003235.887-123.41-0.003244.81836.590.010153.253-143.410.010156.56216.590.01653.478-163.410.01652.905-3.410.01754.505-183.410.01753.123-23.410.009160.809-203.410.009149.161-43.41-0.003247.977-223.41-0.003227.185-63.41-0.003302.558-243.41-0.003280.033最大轨迹偏差为0.02mm,出现在α=5.59°处;最大瞬心偏差为350.060mm,出现在α=-87.41°处。表中α为外弧偏心轴的转角,其轨迹偏差是指结晶器中心点E的轨迹偏差。从表1~3可以看出,机构运动时,其振幅及频率对轨迹偏差和瞬心偏差都有影响,但轨迹偏差仅受振幅的影响而不受振动频率的影响。这是因为振幅的变化导致一个振动周期内结晶器中心点E最大位移发生变化所致,与运动速度无关。而瞬心偏差不仅受振幅的影响,还受振动频率的影响,这是因为瞬心偏差与振动机构各点速度有关,在机构运行时,无论是改变振幅还是改变频率都会使机构各点的速度发生变化。10\n4 瞬心偏差与轨迹偏差之间的关系振动机构瞬心偏差反过来又产生附加轨迹偏差,其关系可由图3加以说明,机构产生瞬心偏差后,其仿弧运动中心由理论上的O点变为实际上的O′点,当取机构振动行程为S时,摆角由φ变为φ′,由(图3)的几何关系,可以推导出由瞬心偏差引起的附加轨迹偏差,为:图3 瞬心偏差对轨迹偏差的影响式中 R′—仿弧运动实际半径,R′=R-ΔS,ΔS为瞬心偏差。 瞬心偏差对机构运动影响甚小,以取振动参数极限值为例,经计算,当振动频率f=180次/min,振幅为±7.5mm时,其最大瞬心偏差为350.06mm,相对误差为3%,而由此引起的轨迹偏差仅为-1.293×10-4mm,几乎可以忽略。其它工况下最大瞬心偏差与之相比要小得多,所引起的轨迹偏差就更小。因此,在建立优化设计数学模型时,可不考虑这个影响。5 振动机构实际运动误差 需要特别指出的是,理论上的轨迹偏差值都不大,以振幅为±10\n7.5mm为例,其最大轨迹偏差仅为0.02mm,一个周期内的波动量是0.037mm。从这个计算结果可知,四偏心轮式振动机构具有较高的仿弧运动精度,从连铸工艺对铸机所提出的要求看,这种误差是允许的。 实际上,振动机构的运动误差远大于理论计算值。1995年11月北科大与攀钢共同组织对攀钢铸机原结晶器振动机构进行过综合测试[2],I流振动机构结晶器运动的仿弧误差最大值为0.3mm左右,Ⅱ流结晶器运动的仿弧误差值为0.5mm以上。1998年,攀钢与北京冶金设备院对一流结晶器振动机构进行过离线测试,其仿弧误差也为0.21mm。实际的仿弧误差过大是引起漏钢的一个重要原因。引起实际仿弧误差过大的根本原因是: (1)各铰接点的间隙过大,理论上的轨迹偏差是原理误差,是假定机构各环节,特别是各铰接点运动副的间隙为零的情况下计算出来的。各个铰接点运动副如存在间隙,其仿弧运动误差一定大于铰接点的间隙。 (2)四个偏心轴的振幅及相位调整误差的影响,四个偏心轴调整不当,偏心轴之间的振幅及相位相差过大,运行时,振动台各点的运动轨迹发生畸变,不仅导致运动轨迹偏差增大,还会使机构产生附加动载荷。 由以上分析可知,对于四偏心轮式振动机构,设计时不仅要求合理的选择机构参数及几何尺寸,以使原理误差尽可能小,还应合理的选择各运动部件的配合间隙,同时,对机械加工、设备装配、调整都应提出严格的要求,才能保证机构具有较高的仿弧运动精度。6 结论 (1)振动机构的轨迹偏差与振幅有关,与振动频率无关,振幅越大,轨迹偏差越大。 (2)振动机构的瞬心偏差与振幅及频率有关,振幅越大,瞬心偏差越大,振动频率越高,瞬心偏差越大。 (3)导向板弹簧的长度对结晶器中心点的轨迹偏差有较大的影响,在安装条件允许的情况下,应选用较长的导向板弹簧。 (4)瞬心偏差会产生附加的轨迹偏差,但数值很小,设计时可不考虑。 (5)振动机构的实际运动误差比理论误差大得多,设计时应设法克服。10\n参考文献:〔1〕 雷天觉,等.连杆机构设计〔M〕.上海:上海科学技术出版社,1995.10.〔2〕 李谋谓,等.攀钢板坯连铸机结晶器振动装置综合测试分析.北京科技大学,1996.4.10\n内蒙古科技大学本科生毕业设计专题论文题目:连铸结晶器振动机构运动误差分析学生姓名:孟凡超学号:专业:机械制造及其自动化班级:机07-1班指导教师:曹丽英查看更多