辽宁省沈阳市第十五中学2013年高中数学论文 图形计算器应用能力测试活动学生 探究出手角度对抛物运动的影响

辽宁省沈阳市第十五中学2013年高中数学论文 图形计算器应用能力测试活动学生 探究出手角度对抛物运动的影响

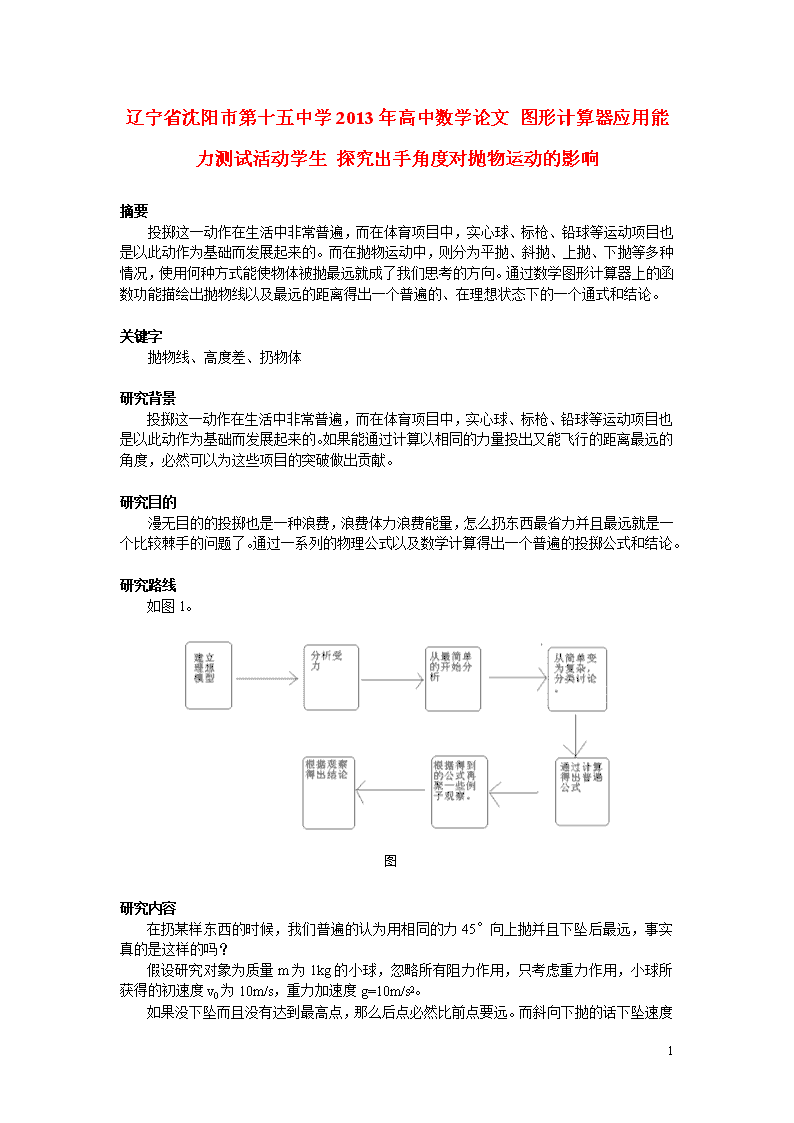
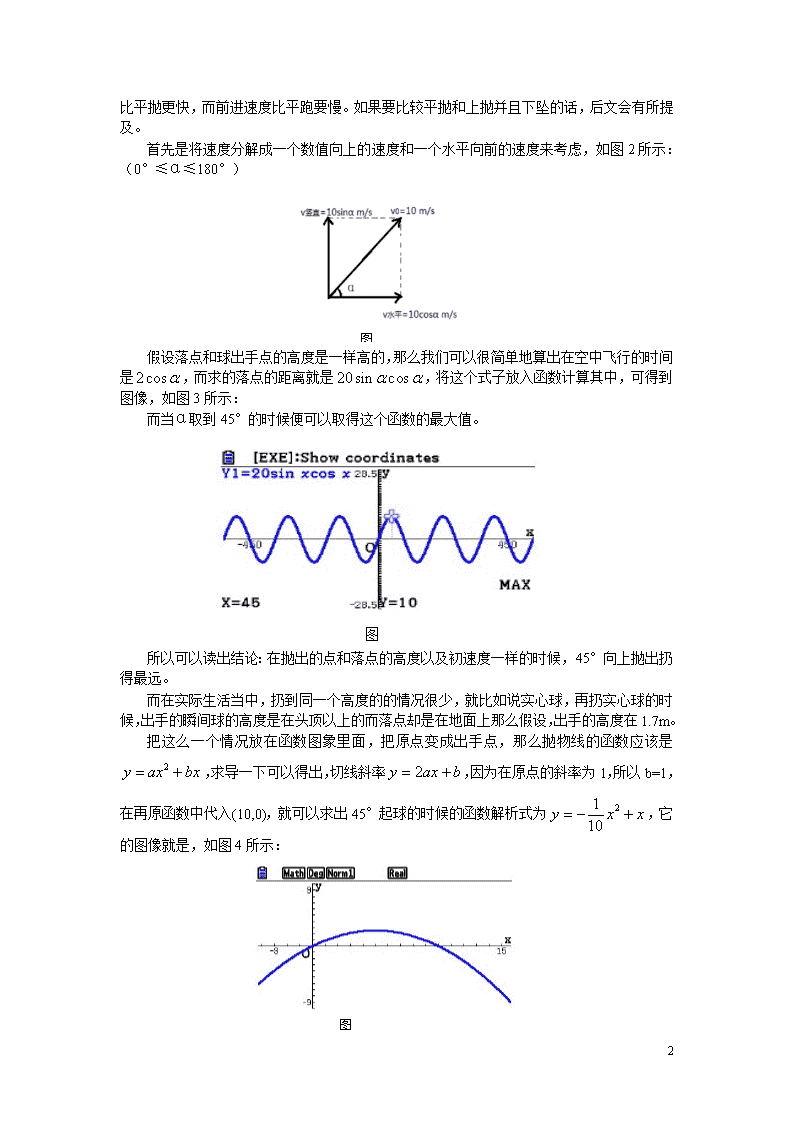
辽宁省沈阳市第十五中学2013年高中数学论文图形计算器应用能力测试活动学生探究出手角度对抛物运动的影响摘要投掷这一动作在生活中非常普遍，而在体育项目中，实心球、标枪、铅球等运动项目也是以此动作为基础而发展起来的。而在抛物运动中，则分为平抛、斜抛、上抛、下抛等多种情况，使用何种方式能使物体被抛最远就成了我们思考的方向。通过数学图形计算器上的函数功能描绘出抛物线以及最远的距离得出一个普遍的、在理想状态下的一个通式和结论。关键字抛物线、高度差、扔物体研究背景投掷这一动作在生活中非常普遍，而在体育项目中，实心球、标枪、铅球等运动项目也是以此动作为基础而发展起来的。如果能通过计算以相同的力量投出又能飞行的距离最远的角度，必然可以为这些项目的突破做出贡献。研究目的漫无目的的投掷也是一种浪费，浪费体力浪费能量，怎么扔东西最省力并且最远就是一个比较棘手的问题了。通过一系列的物理公式以及数学计算得出一个普遍的投掷公式和结论。研究路线如图1。图1研究内容在扔某样东西的时候，我们普遍的认为用相同的力45°向上抛并且下坠后最远，事实真的是这样的吗？假设研究对象为质量m为1kg的小球，忽略所有阻力作用，只考虑重力作用，小球所获得的初速度v0为10m/s，重力加速度g=10m/s2。5\n如果没下坠而且没有达到最高点，那么后点必然比前点要远。而斜向下抛的话下坠速度比平抛更快，而前进速度比平跑要慢。如果要比较平抛和上抛并且下坠的话，后文会有所提及。图2首先是将速度分解成一个数值向上的速度和一个水平向前的速度来考虑，如图2所示：（0°≤α≤180°）假设落点和球出手点的高度是一样高的，那么我们可以很简单地算出在空中飞行的时间是，而求的落点的距离就是，将这个式子放入函数计算其中，可得到图像，如图3所示：图3而当α取到45°的时候便可以取得这个函数的最大值。所以可以读出结论：在抛出的点和落点的高度以及初速度一样的时候，45°向上抛出扔得最远。而在实际生活当中，扔到同一个高度的的情况很少，就比如说实心球，再扔实心球的时候，出手的瞬间球的高度是在头顶以上的而落点却是在地面上那么假设，出手的高度在1.7m。图4把这么一个情况放在函数图象里面，把原点变成出手点，那么抛物线的函数应该是，求导一下可以得出，切线斜率，因为在原点的斜率为1，所以b=1，在再原函数中代入(10,0)，就可以求出45°起球的时候的函数解析式为，它的图像就是，如图4所示：5\n图5将y=-1.7代入，如图5所示：这样就可以求出45°起球的时候可以扔11.48米。当44°起球的时候，可以求出扔的是11.52097米>11048米。所以当起球高度和落点高度不一致的时候，45°不是扔得最远的。那么这个时候几度起球是最远的呢？设x°起球最远，根据物理学公式可以得出扔出去的距离是得到图像并可以读出大约40°的时候扔出去最远。而通过一系列的物理公式我们可以表达出当落点距离起点所在的平面的距离是h（若在起点以上则为负）时，扔出去距离y是：图7图6将h=-3、-1，0，1，2，3代入成为6个函数图像，如图6~11所示：5\n图11图10图9图8由此可以看出来，起点越高，扔出最大距离的合适角度越小。当h<0时，450时,00时,00时,0

查看更多