基于matlab物体运动的描述

基于matlab物体运动的描述

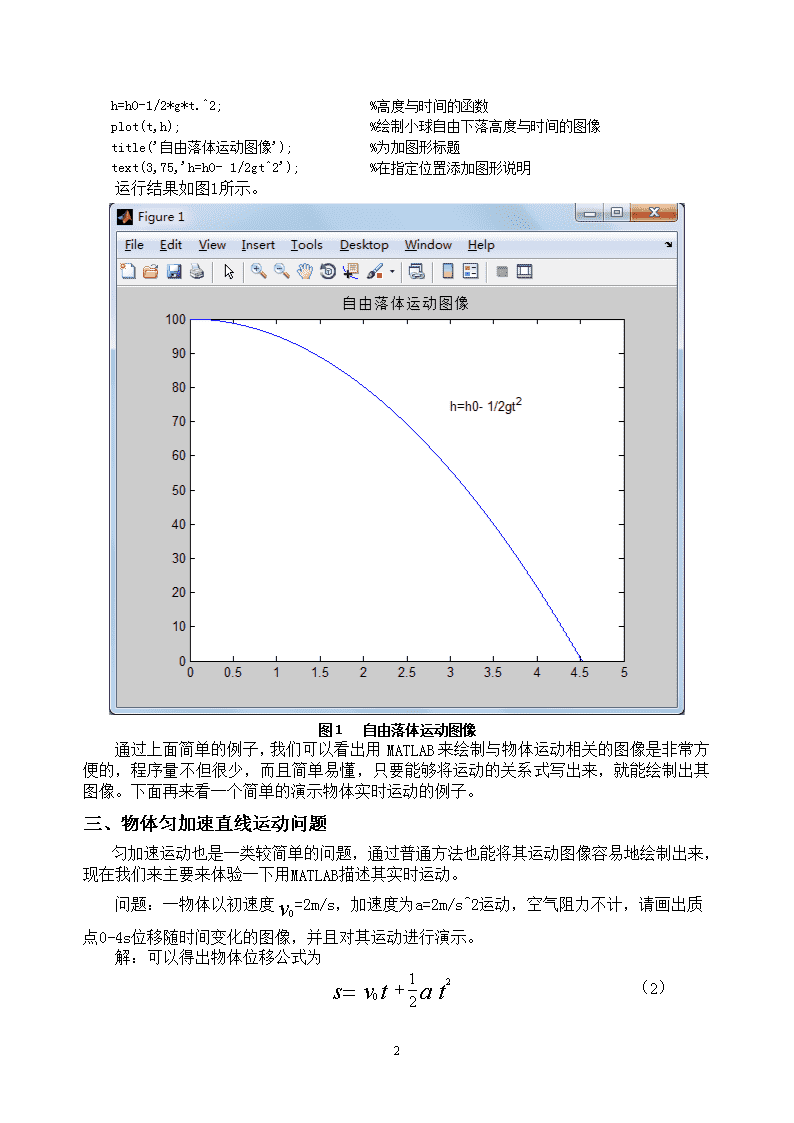
《MATLAB语言》课程论文基于MATLAB物体运动的描述姓名：张凯俭学号：12010245338专业：通信工程班级：通信班指导老师：汤全武学院：物理电气信息学院完成日期：2011.12.915\n基于MATLAB运动物体的描述（张凯俭120102453382010级通信班）[摘要]宇宙中没有绝对静止的物质，凡是物质都在运动。世界上的各种现象都是物质运动的表现形式，按照低级到高级的发展顺序，物质运动分为：机械运动、物理运动、化学运动、生物运动、社会运动五种基本形式，其中尤以物理学中物体的运动最为重要，因为它是事物相互联系的基础。在物理学中我们时常研究物体的运动，主要是用理论物理和实验物理来研究，但是理论物理只能定性和定量地研究，不能直观地将其具体的运动描述出来，实验物理也有一定的局限性，而MATLAB正能够解决这一问题，它不但可以定量地计算，还可以描述任何物体的运动，包括其运动图像和对运动的实时演示，将抽象问题形象直观地表达出来，有助于人们理解，MATLAB解决问题程序量少、简单易懂可以实现大众化，大大提高了工作和学习效率。[关键词]运动MATLAB语言实时演示图形绘制一、问题的提出物理学中物体运动模型是非常抽象的，但是它非常的重要，对解决实际问题有很大的帮助，而MATLAB语言可以非常容易地演示这些模型，使其具体化，相比其它诸如Mathematica、Maple、C、VB等类的语言来说，被称作为第四代计算机语言的MATLAB语言影响大、流行广、函数资源丰富、语法规则简单，以其更加贴近人的思维方式使编程人员从繁琐的程序代码中解放出来，大大提高了效率。MATLAB1984年由美国MathWorks公司推出，它既具有结构化的控制语句（如for循环、while循环、break语句和if语句），又有面向对象编程的特性，不但运算符丰富、程序的可移植性很好，基本上不做修改就可以在各种型号的计算机和操作系统上运行，而且它的图形功能和工具箱十分强劲，被广泛应用于线性代数、自动控制理论、数字信号处理、时间序列分析、动态系统仿真、图像处理等诸多课程的基本教学工具，成为大学生、研究人员和开发人员必须掌握的基本技能。下面我们就应用它来描述几种物体运动的问题.二、自由落体运动问题落体运动在生活中是处处存在的，我们时常会见到它，在物理学中也能非常容易地绘制出它的s-t图形和v-t图形，下面我们就以这个简单的例子来体验一下MATLAB描绘图形的简洁性，直观性。问题：一个小球，质量为1kg，从高=100m的高空自由下落，当地重力加速度，请画出小球离地高度随时间变化的图像。解：不难看出小球离地高度随与时间的函数为（1）MATLAB编写程序如下:clc;clear;%清空命令行h0=100;%定义初始高度常量g=9.8;%定义加速度常量t0=abs(sqrt(h0*2/g));%求落地时间t=0:0.001:t0;%产生时间行向量15\nh=h0-1/2*g*t.^2;%高度与时间的函数plot(t,h);%绘制小球自由下落高度与时间的图像title('自由落体运动图像');%为加图形标题text(3,75,'h=h0-1/2gt^2');%在指定位置添加图形说明运行结果如图1所示。图1自由落体运动图像通过上面简单的例子，我们可以看出用MATLAB来绘制与物体运动相关的图像是非常方便的，程序量不但很少，而且简单易懂，只要能够将运动的关系式写出来，就能绘制出其图像。下面再来看一个简单的演示物体实时运动的例子。三、物体匀加速直线运动问题匀加速运动也是一类较简单的问题，通过普通方法也能将其运动图像容易地绘制出来，现在我们来主要来体验一下用MATLAB描述其实时运动。问题：一物体以初速度=2m/s，加速度为a=2m/s^2运动，空气阻力不计，请画出质点0-4s位移随时间变化的图像，并且对其运动进行演示。解：可以得出物体位移公式为（2）15\n分别将题目中所给参数带入可得（3）用物理学方法可很容易的在草稿纸上画出。下面我们用MATLAB画出它的位移随时间变化的图像。MATLAB编写程序如下:t=0:0.001:4;%定义时间t以0.001为步长，从0到4秒v=2;%定义初速度为2m/sa=2;%定义加速度为2m/s^2s=v*t+1/2*a*t.^2;%定义位移s与时间t的函数plot(t,s)%绘制位移与时间函数的图像title('匀加速直线运动图像');%为加图形标题text(2,8,'s=2t+t^2');%在指定位置添加图形说明运行结果如图2所示。图2匀加速直线运动图像可以看出用MATLAB绘制位移—时间图像非常简单明了，再来看用MATLAB来演示小球真实的运动及其轨迹。MATLAB编写程序如下:v0=2;%定义初速度a=2;%定义加速度15\nt=0:0.001:4;%定义一个以0.001为步长，从0到4秒的时间行向量y=2;%任意去一个常数，方便小球运动演示x=v0*t+1/2*a*t.^2;%得到小球运动轨迹的位移坐标数值i=0;%定义变量并赋初始值fort=0:4/400:4;%利用for循环演示小球运动i=i+1;%变量递增x(i)=v0*x(i)+1/2*a*x(i).^2;%得到小球位移随时间变化的坐标值m=plot(x,y,x(i),y,'or');%绘制小球轨迹和在某时刻的图像，以小圆圈表示小球set(m,'LineWidth',6)%加粗小圆圈title('小球匀加速直线运动演示')%为图形加标题axisequal%纵横坐标轴采用等长刻度axisoff%取消坐标轴getframe;%截取每一幅画面，以便演示动画效果end%for结束运行结果如图3所示。图3小球匀加速直线运动演示截图通过以上简单问题的程序及运行结果我们可以看出用MATLAB不但可以描述物体运动的位移随时间变化图像，还可以描述物体运动轨迹和实时演示物体运动，所以运用MATLAB描述物体运动非常方便、直观，15\n而且简单、明了。当熟练运用MATLAB后，我们可以描述任意物体的运动，以便于解决生活中、学习中、工作中的各种物体运动问题。下面我们来看几个较复杂的问题。四、圆周运动问题物理学中，有一章内容专门介绍圆周运动，可见其在物理学中的重要地位，但是在学习过程中我们只能从书上学习到关于它的几个基本公式如：（4）（5）（6）但是缺乏对其实时运动的演示，不能直观地理解它，所以下面我们对圆周运动进行编写程程序，演示它的运动。问题：请用MATLAB对小球圆周运动进行演示MATLAB编写程序如下:clc;clear;%清空命令行n=200;%定义n=200t=0:pi/n:2*pi;%产生以pi/n为步长，从0到2*pi的行向量x=cos(t);%得到横坐标x的数值y=sin(t);%得到纵坐标y的数值k=0;%对k赋初始值0fort=0:pi/n:2*pi%利用for循环演示小球运动过程k=k+1;%变量递增x(k)=cos(t);%得到横坐标x（k）的数值y(k)=sin(t);%得到纵坐标y（k）的数值m=plot(x,y,x(k),y(k),'or');%绘制小球和其运动轨迹，以红色小圆圈表示小球line([0,x(k)],[0,y(k)],'Color','k','LineStyle',':');%从圆心到球心的跟踪直线axisequal%纵、横做标注采用等长刻度axisoff%取消坐标轴getframe;%截取每一幅画面，以便演示动画效果end%for循环结束运行结果如图4所示。通过上面例子，可看出圆周运动通过MATLAB能够容易地演示出来，直观、形象。五、抛体运动问题抛体运动的范围应用比较广，特别是应用在军事领域的投掷炮弹、发射导弹等，这就需要对整个抛出过程进行精密的计算，但是计算是一方面，要是能够将其过程演示出来会更有助于人们对其理解和操控。所以我们来用MATLAB对抛体运动进行演示。抛体运动分为平抛、斜抛、和竖直上抛，我们可以将其综合到一起，编写一个总的程序，使其能够应用于任何抛体运动，只要人工输入初始速度和发射角即可演示出其运动过程，请看下面问题：问题：小球初速度为，将它以与水平线夹角为α角斜向上抛起，请演示其运动情况。15\n图4圆周运动演示截图MATLAB编写程序如下:v0=input('v0为?');%定义初始速度，并且要求输入初始速度jiaodu=input('物体初始角度为：');%定义物体初始角度，并且要求输入角度g=input('重力加速度为？');%定义重力加速度，并且要求输入重力加速度tt=2*(v0*sin(jiaodu*pi/180))/g;%求物体落地时间t=linspace(0,tt);%产生从开始到落地的时间行向量x=v0*cos(jiaodu*pi/180)*t;%得到水平位移的坐标数值y=v0*sin(jiaodu*pi/180)*t-0.5*g*t.^2;%得到竖直位移坐标数值j=0;%定义变量j，并赋予初始值为0fort=linspace(0,tt)%利用for循环来演示抛体运动j=j+1;%变量递增x(j)=v0*cos(jiaodu*pi/180)*t;%得到物体在某一时刻的水平位移数值y(j)=v0*sin(jiaodu*pi/180)*t-0.5*g*t.^2;%得到物体在某一时刻的竖直位移数值m=plot(x,y,x(j),y(j),'or');%绘制物体运动轨迹和在某时刻的位置，以小圆圈代表小球set(m,'LineStyle',':','LineWidth',2);%改变小球和运动轨迹的线型和宽度xlabel('水平距离/m')%为横坐标添加说明ylabel('高度/m')%为纵坐标添加说明15\ntitle('抛体运动演示')%为图形添加标题getframe;%截取每一幅画面，以便演示动画效果end%for循环结束运行结果如下：v0为?20%回车物体初始角度为：60%回车重力加速度为？9.8%回车运行图形如图5所示。图5抛体运动演示截图上述抛体程序可实现范围较广的抛体运动，可见MATLAB可以应用于较广的范围，只需要改变初始条件就能够很好地体现其通用性。六、简谐、阻尼振动问题（7）可知其是简谐振动最基本的运动学方程,在我们学习简谐振动过程中，根据传统公式，在计算中只知道用振幅、角速度、和初相位来带公式，在画图过程中，只知道它的图形是正弦或余弦曲线，不能较准确地画出其图形，所以我们采用MATLAB来绘制其图形。下面我们来看一个用MATLAB来画其图形的例子。问题：有15\n一定质量的小球系一轻质弹簧的一段，弹簧的另一端系在固定不动的挡板上，让小球在光滑的平面上向一段运动，振幅为A，周期为T，出相位为φ，根据已知量来描述小球的运动轨迹。MATLAB程序编写如下：A=input('请输入振幅=？');%定义振幅，并要求输入omiga=input('请输入角频率=？')%定义角频率，并要求输入xw=input('请输入出相位=？');%定义出相位，并要求输入t=0:0.05*pi:4*pi;%产生以0.05*pi为步长，从0到4*pi的时间行向量x=A*sin(omiga*t+xw);%建立表达式并计算plot(t,x);%绘制图形title('小球简谐振动轨迹图形');%添加图形标题text(pi,0.4,'X=Asin(omiga*t+xw)');%在指定位置为图形添加标注运行结果如下：请输入振幅=？1%回车请输入角频率=？1%回车请输入出相位=？0.1*pi%回车运行图形如图6所示：图6小球简谐振动轨迹图形在我们初次学习指点的简谐运动时，往往存在一种迷茫感，只看到抽象的公式，再就是根据几个已知量来算出其他相关量，而不能清晰地想象的小球的运动轨迹，通过以上程序及图形我们可以看出运用MATLAB可以绘画出清晰的小球运动轨迹图。阻尼运动可以看做是一种能量逐步衰减的的简谐振动，但是其确实比较抽象的，15\n单单地只依靠脑子想象是不容易的，因此我们可以依靠MATLAB强大的绘图功能来演示其，做到将抽象的概念具体化。问题:一个弹簧一端固定在天花板上，另一端与小球链接，请用MATLAB简单地演示小球的实际振动情况。MATLAB编写程序如下：rectangle('position',[12,8,3,0.3],'FaceColor',[0.1,0.3,0.4]);%生成固定弹簧的天花板axis([0,15,-1,10]);%设置坐标轴范围holdon;%保持原有图形plot([13,13],[7,8],'k','linewidth',2);%画与弹簧连接的线，设置为黑色，并且设直线宽为2y=2:.2:7;%得到弹簧对应的纵坐标数据L=length(y);%获取数据的长度x=12+mod(1:L,2)*2;%生成弹簧的横坐标数据x(1)=13;x(end-3:end)=13;%计算出弹簧上下端点的横坐标值A=plot(x,y,'k')%画出黑色弹簧B=0:0.01:2*pi;%生成圆球的角度数据r=0.2;%设置圆球的半径为0.2i1=r*sin(B);%计算出圆球对中心的纵坐标数据Y1=fill(13+r*cos(B),2+i1,'r');%画出圆球set(gca,'ytick',[0:2:9]);%设置y轴的刻度set(gca,'yticklabels',num2str([-1:3]'));%重新设置y轴的刻度值plot([0,15],[2,2],'black');%画出平衡位置H1=plot([0,13],[2,2],'y');%跟踪球心的直线，设置为黄色Q=plot(0,2.5,'color','r');%画出运动曲线;Td=[];%记录时间的变量yd=[];%记录y轴位置的变量T=0;%设置初始时的时间值text(2,8,'弹簧阻尼运动演示','fontsize',24);%添加标注文字set(gcf,'doublebuffer','on');%设置渲染效果whileT<12;%利用whilie循环处理阻尼运动过程pause(0.2);%为显示动画效果而暂停一下Dy=1-0.5*exp(-T/4)*cos(pi*T);%计算T时刻弹簧对平衡位置的位移Y=-(y-2)*Dy+7;%计算弹簧的纵坐标数值Yf=Y(end)+t1;%计算圆球的纵坐标数值Td=[Td,T];yd=[yd,Y(end)];%更新运动曲线的数据set(A,'ydata',Y);%更新弹簧的位置数据set(Y1,'ydata',Yf,'facecolor',rand(1,3));%更新圆球的位置数据set(H1,'xdata',[T,13],'ydata',[Y(end),Y(end)]);%更新跟踪线的数据set(Q,'xdata',Td,'ydata',yd);%更新圆球的数据T=T+0.1;%更新时间endKd=find(diff(sign(diff(yd)))==-2)+1;%计算极大值的位置X=Td(Kd);%得到极大值处的横坐标数值Y=yd(Kd);%得到极大值处的纵坐标数值15\nX=[0,X,Td(end)];%得到上侧包络线的横坐标数据Y=[yd(1),Y,yd(end)];%得到上侧包络线的纵坐标数据plot(X,Y,':');%画出上侧包络线Kx=find(diff(sign(diff(yd)))==2)+1;%计算极小值的位置X=Td(Kx);%得到极小值处的横坐标数值Y=yd(Kx);%得到极小值处的纵坐标数值X=[0,X,Td(end)];%得到下侧包络线的横坐标数据Y=[-(yd(1)-4),Y,-(yd(end)-4)];%得到下侧包络线的纵坐标数据plot(X,Y,':');%画出下侧包络线运行结果如图7所示。图7弹簧阻尼运动演示截图通过程序和运行结果我们就可以容易地理解弹簧的阻尼运动，将抽象概念具体化。七、螺旋曲线运动物体沿螺旋线运动虽然是一种比较陌生的物理学模型，在学习过程中不经常接触到它，但其作为模型说明问题确是非常必要的，它可以说明很多复杂的问题。可是如果不能将其具体化，理解起来会有一定的困难，下面通过MATLAB来演示其运动情况，帮助理解。问题：请演示一个小球沿封闭螺旋线运动情况。MATLAB编写程序如下：functioncs=zkj(k,ki);%此函数演示红色小球沿一条封闭螺旋曲线运动,k为小球循环数15\nt1=(0:1000)/1000*10*pi;%产生具有1001个元素的行向量z1=cos(t1);%得到坐标z1的数值y1=sin(t1);%得到坐标y1的数值x1=-t1;%得到x1的数值t2=(0:10)/10;%产生具有11个元素的行向量x2=x1(end)*(1-t2);%将x1末尾元素与t2行向量倒序相乘的值赋给x2y2=y1(end)*(1-t2);%将y1末尾元素与t2行向量倒序相乘的值赋给y2z2=z1(end)*ones(size(x2));%产生与x2同维数的全1矩阵，并且将其与z1的末尾元素相乘的值赋给z2t3=t2;%将t2赋给t3z3=(1-t3)*z1(end);%将z1末尾元素与t3行向量倒序相乘的值赋给z3x3=zeros(size(z3));%产生与z3同大小的全0矩阵x3y3=x3;%将矩阵x3赋给y3t4=t2;%将t2赋给t4x4=t4;%将t4赋给x4y4=zeros(size(x4));%产生与x4同大小的全0矩阵y4z4=y4;%将y4赋给z4x=[x1,x2,x3,x4];%x1、x2、x3、x4组成矩阵xy=[y1,y2,y3,y4];%y1、y2、y3、y4组成矩阵yz=[z1,z2,z3,z4];%z1、z2、z3、z4组成矩阵zplot3(x,y,z,'color',[1,0.6,0.4],'linewidth',2.5)%绘制小球运动的x、y、z三维函数并改变图形颜色和线宽view(30,10);%指定图形视点axisoff%取消坐标轴title('小球沿封闭螺旋线运动演示')%为图形添加标题h=line('xdata',x(1),'ydata',y(1),'zdata',z(1),'color',[1,0,0],'Marker','.','MarkerSize',40,'EraseMode','xor')%定义小球的颜色、点形、大小和擦除方式n=length(x);%将x的长度存入ni=1;j=4;%定义变量i、jwhile1%用while循环控制小球运动set(h,'xdata',x(i),'ydata',y(i),'zdata',z(i));%设置三个坐标轴属性drawnow;%刷新屏幕pause(0.0005)%暂停一下i=i+1;%变量加1ifnargin==2&nargout==1%if语句，判断条件是否成立if(i==ki&j==1);f=getframe(gcf);%if语句，判断条件是否成立，若成立，则截取当前画面信息end%内嵌if语句结束end%if语句结束ifi>n%判断小球是否运动到螺旋线终点i=1;j=j+1;%到终点时返回，做下一次运动，并且已循环次数加1ifj>k;break;%若j大于循环次数k，则循环停止end%内嵌if语句结束end%if语句结束15\nend%while循环结束调用时输入下列命令:cs=zkj(10,2000);运行结果如图8所示。图8小球沿封闭螺旋线运动演示截图观看了以上运行结果后，我们就可以很容易地理解螺旋线运动了。下面看一个物理学运动用数理方法解得问题。八、有界弦振动问题有界弦振动在数理方程中是一类比较常见的问题，众所周知，它是比较复杂的，非常抽象，让人理解起来有很大的困难，特别是求其解析解，很多人也许可能会求出解，但是始终不能在脑子里形成一种具体的图像，不知道它到底是什么样的，下面我们就用MATLAB来绘出它解的分布，以描述其振动情况。问题：解下列有界弦振动方程，并用MATLAB绘制其解的图像（8）（9）（10）15\n解：可得解析解为（令系数为1）：（11）可看出此问题的解是很复杂的，因此我们需要用MATLAB来解决此问题。n=1本振解随时间变化的图形分布MATLAB编写程序为：cleara=1;l=1;x=0:0.05:1;t=0:0.001:3;u=0;n=1;%函数参数[X,T]=meshgrid(x,t);%函数变量u=(cos(n*pi*a*T/l)+sin(n*pi*a*T/l)).*sin(n*pi*X/l);%函数定义式figure(1)%控制窗口数量axis([01-0.050.05])%图形取点，x分布mesh(X,T,u);%绘制三维网格图title('n=1本振随时分布的透视图')%添加图形标题xlabel('x')%图像坐标轴'x'ylabel('t')%图像坐标轴'y'zlabel('u')%图像坐标轴'u'运行结果如图9所示。图9n=1时本振随时分布的透视图n=2本振解随时间变化的图形分布MATLAB编写程序为：clear15\na=1;l=1;x=0:0.05:1;t=0:0.001:3;u=0;n=2;%函数参数[X,T]=meshgrid(x,t);%函数变量u=(cos(n*pi*a*T/l)+sin(n*pi*a*T/l)).*sin(n*pi*X/l);%函数定义式figure(1)%控制窗口数量axis([01-0.050.05])%图形取点，x分布mesh(X,T,u);%绘制三维网格图title('n=2本振随时分布的透视图')%添加图形标题xlabel('x')%图像坐标轴'x'ylabel('t')%图像坐标轴'y'zlabel('u')%图像坐标轴''u'运行结果如图10所示。图10n=2时本振随时分布的透视图通过以上程序和运行结果可以看出我们能将一个非常复杂的数理方程问题直观的描述出来，这样不但可以加深印象，而且可以很容易的理解这类复杂的问题。九、结论通过以上基于MATLAB描述的几种物体的运动情况，我们很容易得出以下结论：1.MATLAB解决物理运动学图像的绘制问题非常简单，即使是数理方程中复杂的有界弦振动问题，它省去了手工直接绘制简单图形和间接绘制复杂图形的繁琐，只需简单地对公式进行编程就可以绘制出所需图像，其简洁直观性不言而喻。15\n2.MATLAB对物体运动情况进行实时演示直观、明了、真切，特别是对一些比较复杂的物体运动（螺旋线运动、阻尼振动）的演示非常逼真。它所编写的程序量少，克服了其它语言程序的繁杂性，简单易懂。MATLAB函数功能强大、定义简单，格式自由，使用灵活、不局限，非常有利于将我们所接触到的抽象事物具体化，确实是我们工科学生非常好的一种工具。十、课程体会时光飞快，转眼间已至学期末，在这一学期对学业的艰苦求索中，老师和同学们给了我很多帮助。首先感谢我的指导老师汤老师，教会了我很多，让我懂得了MATLAB许多的优点，也感谢我的同学，给予我很大的帮助，他们我学到了许多知识，尤其是接触到了一门新语言——MATLAB。以前也学过一门计算机语言，那就是C语言，但是在学习C语言的过程中，碰到了很多的困难，它的题目繁多，而且程序量非常大，逻辑性非常强，格式局限不自由，一道题目如果少个分号都会出现错误，致使运行不出来。接触到了MATLAB后我才发现在运算符、结构化语句、函数等很多方面MATLAB不但可以与其它语言相抗衡，而且在程序量、程序设计自由度、程序移植性等方面远远优于其他语言。在每次实验课结束后，我都会体验到MATLAB新的功能。八次的实验课和这次课程设计让我深深认识到矩阵实验室——MATLAB不但对线性代数矩阵的分析与处理有着强大的功能，而且其选择结构、循环结构程序的设计和函数文件的应用是非常方便，尤其是它的低层绘图、高层绘图以及动画的制作中的函数非常简单实用，很容易地就可以将一个非常复杂的图形和动画以编写较小的程序而演示出来，可以大范围地应用于各个学科，帮助学习。时代在发展，社会在进步，科学技术越来越发达，随之而出现的问题也就越来越多、越来越难，那么在许多领域研究问题就需要更好的工具，而MATLAB这个在11月各种语言排行榜上位居前列的新秀正是我们所需要的，它将在科学发展史上留下抹不去的身影。[参考文献][1]刘卫国.MATLAB程序设计与应用（第二版）[M].北京：高等教育出版社，2006.[2]马文蔚.物理学（第四版）[M].北京：高等教育出版社，1999.[3]豆丁网文献.参考《MATLAB在数学物理方法中的应用》[4]刘卫国.MATLAB程序设计与应用（第二版）Matlab绘图豆丁网[5]陈育宁.数学物理方法.[M].宁夏：人民教育出版社，2008.[6]MATLAB中文论坛网.参考《抛体运动》[7]刘正君.《MATLAB科学计算与可视化仿真宝典》.电子工业出版社,2009.15