基于 matlab 的 puma560 机器人运动仿真与轨迹规划 5

基于 matlab 的 puma560 机器人运动仿真与轨迹规划 5

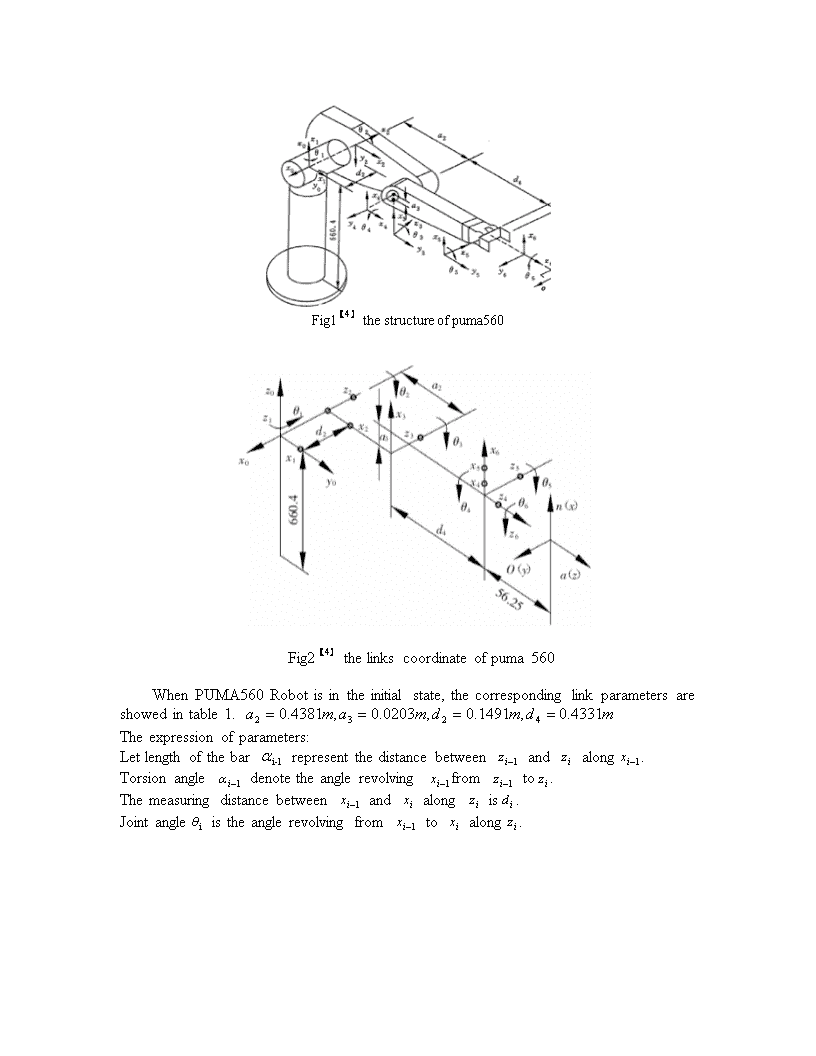
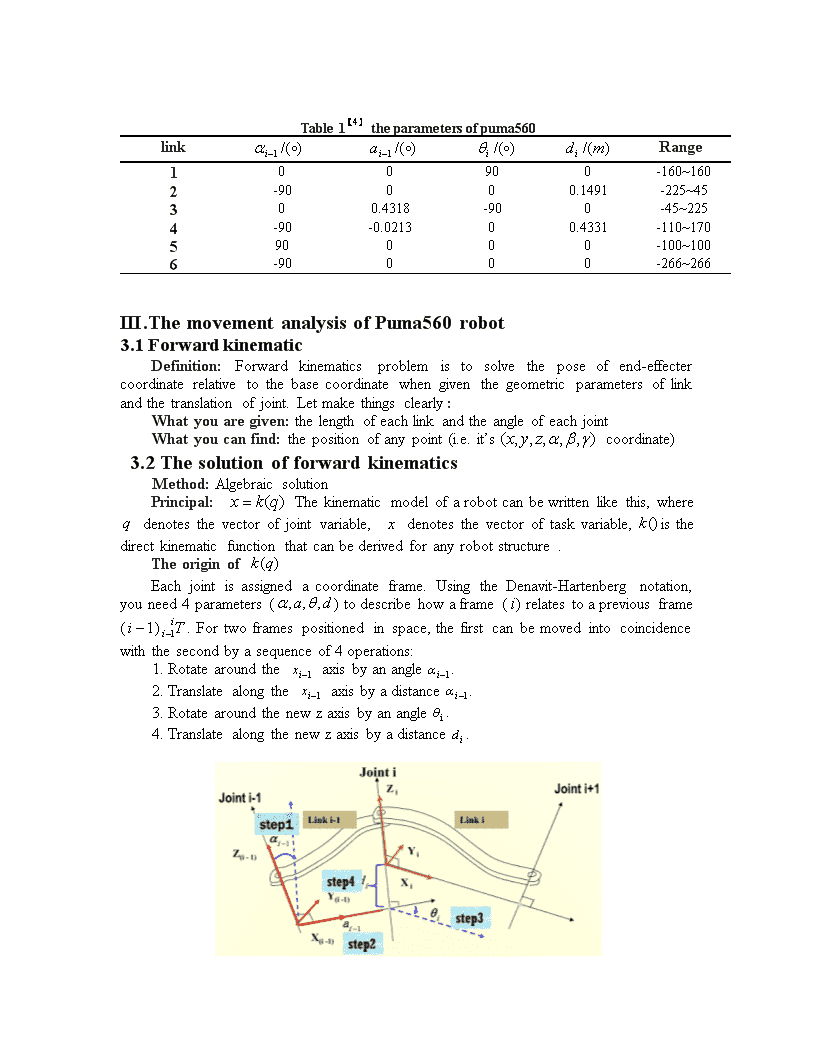
ThemovementsimulationandtrajectoryplanningofPUMA560robotShibozhaoAbstract:Inthisessay,weadoptmodelingmethodtostudyPUMA560robotintheuseofRoboticsToolboxbasedonMATLAB.Wemainlyfocusonthreeproblemsinclude:theforwardkinematics,inversekinematicsandtrajectoryplanning.Atthesametime,wesimulateeachproblemabove,observethemovementofeachjointandexplainthereasonfortheselectionofsomeparameters.Finally,weverifythefeasibilityofthemodelingmethod.Keywords:PUMA560robot;kinematics;RoboticsToolbox;Thesimulation;I.IntroductionAsautomationbecomesmoreprevalentinpeople’slife,robotbeginsmorefurthertochangepeople’sworld.Therefore,weareobligedtostudythemechanismofrobot.Howtomove,howtodeterminethepositionoftargetandtherobotitself,andhowtodeterminetheanglesofeachpointneededtoobtaintheposition.Inordertostudyrobotmorevalidly,weadoptrobotsimulationandobject-orientedmethodtosimulatetherobotkinematiccharacteristics.Wehelpresearchersunderstandtheconfigurationandlimitoftherobot’sworkingspaceandrevealthemechanismofreasonablemovementandcontrolalgorithm.Wecanlettheusertoseetheeffectofthedesign,andtimelyfindouttheshortcomingsandtheinsufficiency,whichhelpusavoidtheaccidentandunnecessarylossesonoperatingentity.ThispaperestablishesamodelforRobotPUMA560byusingRoboticsToolbox,andstudytheforwardkinematicsandinversekinematicsoftherobotandtrajectoryplanningproblem.II.TheintroductionoftheparametersforthePUMA560robotPUMA560robotisproducedbyUnimationCompanyandisdefinedas6degreesoffreedomrobot.Itconsists6degreesoffreedomrotaryjoints(Thestructurediagramisshowninfigure1).Referringtothehumanbodystructure,thefirstjoint（J1）calledwaistjoints.Thesecondjoint（J2）calledshoulderjoint.Thethirdjoint（J3）calledelbowjoints.ThejointsJ4J5,J6,arecalledwristjoints.Where,thefirstthreejointsdeterminethepositionofwristreferencepoint.Thelatterthreejointsdeterminetheorientationofthewrist.TheaxisofthejointJ1locatedverticaldirection.TheaxisdirectionofjointJ2,J3ishorizontalandparallel,a3metersapart.JointJ1,J2axisareverticalintersectionandjointJ3,J4axisareverticalcrisscross,distanceofa4.Thelatterthreejoints’axeshaveanintersectionpointwhichisalsooriginpointfor{4},{5},{6}coordinate.(Eachlinkcoordinatesystemisshowninfigure2)\nFig1thestructureofpuma560Fig2thelinkscoordinateofpuma560WhenPUMA560Robotisintheinitialstate,thecorrespondinglinkparametersareshowedintable1.Theexpressionofparameters:Letlengthofthebarrepresentthedistancebetweenandalong.Torsionangledenotetheanglerevolvingfromto.Themeasuringdistancebetweenandalongis.Jointangleistheanglerevolvingfromtoalong.\nTable1theparametersofpuma560linkRange100900-160~1602-90000.1491-225~45300.4318-900-45~2254-90-0.021300.4331-110~170590000-100~1006-90000-266~266III.ThemovementanalysisofPuma560robot3.1ForwardkinematicDefinition:Forwardkinematicsproblemistosolvetheposeofend-effectercoordinaterelativetothebasecoordinatewhengiventhegeometricparametersoflinkandthetranslationofjoint.Letmakethingsclearly:Whatyouaregiven:thelengthofeachlinkandtheangleofeachjointWhatyoucanfind:thepositionofanypoint(i.e.it’scoordinate)3.2ThesolutionofforwardkinematicsMethod:AlgebraicsolutionPrincipal:Thekinematicmodelofarobotcanbewrittenlikethis,wheredenotesthevectorofjointvariable,denotesthevectoroftaskvariable,isthedirectkinematicfunctionthatcanbederivedforanyrobotstructure.TheoriginofEachjointisassignedacoordinateframe.UsingtheDenavit-Hartenbergnotation,youneed4parameters()todescribehowaframe()relatestoapreviousframe().Fortwoframespositionedinspace,thefirstcanbemovedintocoincidencewiththesecondbyasequenceof4operations:1.Rotatearoundtheaxisbyanangle.2.Translatealongtheaxisbyadistance.3.Rotatearoundthenewzaxisbyanangle.4.Translatealongthenewzaxisbyadistance.\n(1.1)(1.2)Therefore,accordingtothetheoryabovethefinalhomogeneoustransformcorrespondingtothelastlinkofthemanipulator:(1.3)3.3InversekinematicDefinition:Robotinversekinematicsproblemisthatresolveeachjointvariablesoftherobotbasedongiventhepositionanddirectionoftheend-effecterorofthelink(ItcanshowaspositionmatrixT).AsforPUMA560Robot,variableneedtoberesolved.Letmakethingsclearly:Whatyouaregiven:Thelengthofeachlinkandthepositionofsomepointontherobot.Whatyoucanfind:Theanglesofeachjointneededtoobtainthatposition.3.4ThesolutionofinversekinematicsMethod:AlgebraicsolutionPrincipal:WhereistherobotJacobian.JacobiancanbeseenasamappingfromJointvelocityspacetoOperationalvelocityspace.3.5ThetrajectoryplanningofrobotkinematicsThetrajectoryplanningofrobotkinematicsmainlystudiesthemovementofrobot.Ourgoalistoletrobotmovesalonggivenpath.Wecandividethetrajectoryofrobotsintotwokinds.Oneispointtopointwhiletheotheristrajectorytracking.Theformerisonlyfocusonspecificlocationpoint.Thelattercaresthewholepath.Trajectorytrackingisbasedonpointtopoint,buttherouteisnotdetermined.So,trajectorytrackingonlycanensuretherobotsarrivesthedesiredposeintheendposition,butcannotensureinthewholetrajectory.Inordertolettheend-effecterarrivingdesiredpath,wetrytoletthedistancebetweentwopathsassmallaspossiblewhenweplanCartesianspacepath.Inaddition,inordertoeliminateposeandposition’suncertaintybetweentwopathpoints,weusuallydomotivationplanamongeveryjointsundergangcontrol.Inaword,leteachjointhassamerundurationwhenwedotrajectoryplanninginjointspace.\nAtsametime,inordertomakethetrajectoryplanningmoresmoothly,weneedtoapplytheinterpolatingmethod.Method:polynomialinterpolating[1]Given:boundarycondition(1.3)(1.4)Output:jointspacetrajectorybetweentwopoints=（1.5）Polynomialcoefficientcanbecomputedasfollows:(1.6)IV.KinematicsimulationbasedonMATLABHowtouselinkInRoboticsToolbox,function’link’isusedtocreateabar.Therearetwomethods.OneistoadoptstandardD-HparametersandtheotheristoadoptmodifiedD-Hparameters,whichcorrespondtotwocoordinatesystems.WeadoptmodifiedD-Hparametersinourpaper.Thefirst4elementsinFunction‘link’areα,a,θ,d.Thelastelementis0(representRotationaljoint)or1(representtranslationjoint).Thefinalparameteroflinkis’mod’,whichmeansstandardormodified.Thedefaultisstandard.Therefore,ifyouwanttobuildyourownrobot,youmayusefunction‘link’.Youcancallitlikethis:’L1=link([00pi00],'modified');Thestepofsimulationis:Step1:Firstofall,accordingtothedatafromTable1,webuildsimulationprogramoftherobot(showninAppendixrob1.m).Step2:Present3Dfigureoftherobot(showninFig4).Thisisathree-dimensionalfigurewhentherobotlocatedtheinitialposition().Wecanadjustthepositionofthesliderincontrolpaneltomakethejointrotation(inFig5),justlikecontrollingrealrobot.Step3:PointAlocatedatinitialposition.Itcandedescribedas.ThetargetpointisPointB.Thejointrotationanglecanbeexpressedas.Wecanachievethesolutionofforwardkinematics\nandobtaintheend-effecterposerelativetothebasecoordinatesystemis(0.737,0.149,0.326),relativetothethreeaxesofrotationangleisthe(0,0,-1).Therobot’sthree-dimensionalposeinisshowninFig6.Step4:Accordingtothehomogeneoustransformationmatrix,wecanobtaineachjointvariablefromtheinitialpositiontothespecifiedlocationStep5:SimulatetrajectoryfrompointAtopointB.Thesimulationtimeis10s.Timeintervalis0.1s.Then,wecanpicturelocationimage,theangularvelocityandangularaccelerationimage(shownasFig8)whichdescribeeachjointtransformsovertimefromPointAtoPointB.Inthispaper,weonlypresentthepictureofjoint3.Byusingthefunction‘T=fkine(r,q)’,weobtain‘T’athree-dimensionalmatrix.Thefirsttwodimensionalmatrixrepresentthecoordinatechangewhilethelastdimensionistime‘t’.Fig4Fig5\nFig6Fig7\nFig8VTheproblemduringthesimulationThereasonforselectionofsomeparameterTheparameteroflink:Fromkinematicsimulationandprogram,youcanseethatIsetcertainvaluenotarbitrarywhenIcall‘link’.ThatisbecauseIwantthesimulationcanbemoreclosetotherealsituation.So;Iadopttheparameterofpuma560(youcanseeitfromtheprogram)andthereisnodifferencebetweenmyrobotandpuma560radically.Theparameterof:WhenIchoosetheparameterof,Ijustwanttotestsomething.Forexample,whenyoudenotetheparameterof‘’likethis‘’,youwanttousethefunction‘fkine(p560,)’toobtainthehomogenousfunction‘T’,then,youwanttouse‘ikine(p560,T)’totestwhetherthe‘’iswhatyouhavesettledbefore.Theresultisasfollows:=[0-pi/4-pi/40pi/80];T=fkine(p560,);=ikine(p560,T)=[0-pi/4-pi/40pi/80]\nActually,notalloftheparametercandolikethis.Forexample,whenyoutry=[pi/2,pi/2,pi/2,pi/2,pi/2,pi/2],theanswerisnotitself.\nVI.References[1]http://en.wikipedia.org/wiki/Robot_[online],7-ferbury-2015[2]http://www.docin.com/p-947411515.html[online],7-ferbury-2015[3]http://en.wikipedia.org/wiki/Jacobian_algorithm[accessed8-February-2015][4]YoulunXiong,HanDing,EncangLiu,Robot[M],Tinghuauniversitypress,1993VIIAppendixclc;clear;%modified改进的D-H法L1=link([00pi00],'modified');L2=link([-pi/2000.14910],'modified');L3=link([00.4318-pi/200],'modified');L4=link([-pi/20.020300.43180],'modified');L5=link([pi/20000],'modified');L6=link([-pi/20000],'modified');r=robot({L1L2L3L4L5L6});r.name='zhaoshibo';%模型的名称drivebot(r)track.m%前3个关节对机械手位置的影响qA=[0,0,0,0,0,0];%起始点关节空间矢量qB=[0-pi/4-pi/40pi/80];%终止点关节空间矢量t=[0:0.1:10];%仿真时间[q,qd,qdd]=jtraj(qA,qB,t);%关节空间规划plot(r,q)%关节3的角速度、角速度和角加速度曲线figuresubplot(1,3,1)plot(t,q(:,3))%关节3的位移曲线xlabel('时间t/s');ylabel('关节的角位移/rad');gridonsubplot(1,3,2)plot(t,qd(:,3))%关节3的位移曲线xlabel('时间t/s');ylabel('关节的角速度/（rad/s)');gridonsubplot(1,3,3)plot(t,qdd(:,3))%关节3的位移曲线xlabel('时间t/s');ylabel('关节的角加速度/（rad/s^2)');gridon