《生物统计学复习》PPT课件

《生物统计学复习》PPT课件

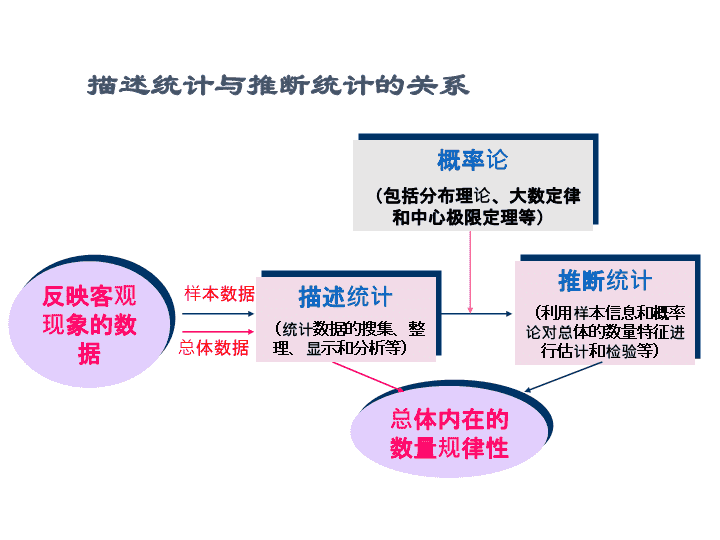
生物统计学总复习2015-06-29\n一、什么是统计学Statistics？统计学是收集、分析、表述和解释统计数据的科学。统计学是关于数据的科学。资料的收集就是取得统计数据。数据整理是将数据分组、归纳和汇总并将其用图表的形式表达出来。数据分析是通过统计方法研究数据，并结合实际背景阐述实际问题的特征的过程。数据解释是对分析结果进行说明。统计学分为描述统计学和推断统计学。\n反映客观现象的数据总体内在的数量规律性推断统计（利用样本信息和概率论对总体的数量特征进行估计和检验等）概率论（包括分布理论、大数定律和中心极限定理等）描述统计（统计数据的搜集、整理、显示和分析等）总体数据样本数据描述统计与推断统计的关系\n几个基本概念总体(population)、个体（individual）与样本(sample)总体（N）：一个统计问题所研究对象的全体有限总体：一个班级学生的身高无限总体：临床试验中来推断某一药品疗效高、某一棉田棉铃虫的头数个体：组成总体的每一基本单元样本（n）：从总体中抽取的部分个体，用于对总体进行推断（n≤30，小样本；n>30，大样本）通过某事物的一部分（样本），来估计事物的全部（总体）特征\nJJJJJJJ\n几个基本概念（续）\n几个基本概念（续）变量(variable)与观测值(observation)变量（变数）：相同性质的事物表现差异性的某种特征，其表现随个体而异身高、体重、叶绿素含量、叶片形状随机变量：变量取值的变化是不可预测的变量通常记为：x，y，z，…观测值：对变量进行测量或观察所获得的数值观测值也称为：变量值（valueofvariables）、资料/数据（data）\n二、均值和方差：第i个观察值或变数n：观察值或变数的个数∑：求和符号（sigma）计算公式：\n标准差和方差总体方差和总体标准差样本方差和样本标准差\n三、概率与概率分布概率分布-几个概念概率函数(probabilityfunction)随机变量取某一特定值的概率函数（离散型随机变量）二项分布（对立事件）和泊松分布(出现概率较小，样本容量大)概率密度函数(probabilitydensityfunction)随机变量取某一特定值的密度函数（连续型随机变量）概率分布函数(probabilitydistributionfunction)随机变量取值小于或等于某特定值的概率\n离散型随机变量的概率分布概率分布图\n概率分布函数累积函数密度函数连续型随机变量的密度函数及概率分布函数x=某一特定值时，P=0\n13若n→∞，二项分布连接线表现为一个光滑的曲线。这一曲线称之为正态分布曲线或正态概率曲线。其概率密度函数为：记做：N(μ,σ2)\n14由于正态曲线受μ和σ的制约，曲线随这两个参数的变化而改变。构造一个新变数，这个变数要消去μ和σ的影响。假定新变数用u来表示，则：标准正态分布的概率密度函数u变换标准正态分布u服从均数为0、标准差为1的正态分布\n\n16原总体样本1样本2样本n新总体n统计量如果从容量为N的总体抽样（放回），若每次抽取容量为n的样本，那么一共可以得到Nn个样本。每个样本可以计算一个平均数，如果将这些平均数集合起来便构成一个新总体。由于每次随机抽样所得的平均数可能会存在差异，所以由平均数构成的新总体也应该有其分布，这种分布称为平均数的抽样分布。样本均值的抽样分布\n1、样本平均数的期望值由于不同的样本可得到不同的样本均值，因此，考察样本均值的期望就显得非常重要。用表示样本均值的期望值，表示总体均值，可证明在简单随机抽样中。2.样本平均数的标准差称为标准误。\nt分布当总体标准差σ未知时，且样本数小于30时,以样本标准差S代替σ所得到的统计量记为t。在计算时，由于采用S来代替σ，使得t变量不再服从标准正态分布，而是服从t分布服从自由度为n-1的t分布\n2、t分布密度曲线以纵轴为对称轴，左右对称，且在t＝0时，分布密度函数取得最大值3、与标准正态分布曲线相比,t分布曲线顶部略低，两尾部稍高而平.df越小这种趋势越明显.df越大，t分布越趋近于标准正态分布.当n>30时，t分布与标准正态分布的区别很小；n>100时，t分布基本与标准正态分布相同；n→∞时，t分布与标准正态分布完全一致正态分布曲线与t分布曲线的比较t分布的特征1、t分布受自由度df=n-1的制约，每一个自由度都有一条t分布密度曲线\nＦ分布设从一正态总体中随机抽取样本容量为n，m的两个独立样本,其样本的方差为，则定义两者的比值为F：服从自由度为n-1,m-1的F分布\nF分布特征1)F分布的平均数μ＝1，F的取值区间为[0，+∞)2)F分布曲线的形状仅决定于df1和df2.在df1＝l或2时,F分布曲线呈严重倾斜的反向J型，当df1>=3时转为左偏曲线(在平均值的左边)不同自由度下的F分布曲线\n四、统计推断统计推断由一个样本或一糸列样本所得的结果来推断总体的特征假设检验参数估计原理：概率很小的事件在一次抽样试验中实际是几乎不可能发生的。=0.05/0.01\n假设检验（Hypothesis）如何进行检验：样本平均数总体均数推断样本随机抽样总体\n1、提出假设对立无效假设/零假设/检验假设备择假设/对应假设0＝0误差效应处理效应H0HA\n2、确定显著水平＝0.05显著水平*极显著水平**能否定H0的人为规定的概率标准称为显著水平，记作。统计学中，一般认为概率小于0.05或0.01的事件为小概率事件,所以在小概率原理基础上建立的假设检验也常取=0.05和=0.01两个显著水平。P<＝0.01＝0.05\n3、选定检验方法，计算检验统计量，确定概率值u=x-x136-126=√40=1.581P(u>1.581)=2×0.0571=0.1142根据研究设计的类型和统计推断的目的选择使用不同的检验方法。本例：服从N(x,x2)分布。例：\n4、作出推断结论：是否接受假设P>P<小概率原理接受H0否定HA否定H0接受HA可能正确可能错误\nu0.05=1.64u0.01=2.33单尾检验分位数双尾检验分位数u0.05=1.96u0.01=2.58２２否定区否定区否定区接受区接受区查表时，单尾概率乘以2等于双尾概率＞\n大样本平均数的假设检验－－u检验小样本平均数的假设检验－－t检验单样本双样本样本平均数的假设检验\n1、总体方差σ2已知，无论n是否大于30都可采用u检验法。2、总体方差σ2未知，但n>30时，可用样本方差s2来代替总体方差σ2，仍用u检验法。3、总体方差σ2未知，且n<30时，可用样本方差s2来代替总体方差σ2，采用df=n-1的t检验法。应用情景：\n试验设计成组数据平均数的比较成对数据平均数的比较分到两个组中的数据，没有关系，相互独立。两个样本平均数的假设检验将性质相同的两个样本（供试单位）配偶成对，每一对除随机地给予不同处理外，其他试验条件应尽量一致，排除实验单位不一致对实验结果的影响。\n1、两个总体方差σ12和σ22已知，或σ12和σ22未知，但两个样本都是大样本，即n1>30且n2>30时，用u检验法。2、两个总体方差σ12和σ22未知，且两个样本都是小样本，即n1<30且n2<30时，用t检验法。成组数据平均数的比较-应用情景成对数据平均数的比较略\n所谓方差的同质性，就是指各个总体的方差是相同的。方差的同质性检验就是要从各样本的方差来推断其总体方差是否相同方差的同质性检验\n五、方差分析t检验可以判断两组数据平均数间的差异显著性对多个处理进行平均数差异显著性检验时，采用t检验法的缺点：方差：又叫均方，是标准差的平方，是表示变异的量。\n确定各种原因在总变异中所占的重要程度。处理效应试验误差相差不大，说明试验处理对指标影响不大。相差较大，即处理效应比试验误差大得多，说明试验处理影响是很大的，不可忽视。xij=μ+τi+εij(i=1,2,3…,k；j=1,2,3…,n)μ－总体平均数τi－处理效应εij－试验误差xij－是在第i次处理下的第j次观测值\n多重比较（multiplecomparisons）要明确不同处理平均数两两间差异的显著性，每个处理的平均数都要与其他的处理进行比较，这种差异显著性的检验就叫多重比较。即：统计上把多个平均数两两间的相互比较称为多重比较。概念五、多重比较\n多重比较方法较多（multiplecomparisons）\n不同离子对木聚糖酶活性的影响(mg/ml)0.000.250.500.751.001.250.000.060.120.180.240.300.000.400.801.201.602.000.000.400.600.801.001.20Na+K+Cu2+Mn2+水平实验指标因素***对多因素试验而言，处理就是指水平与水平的组合\n定义：是指对试验指标同时受到两个试验因素作用的试验资料的方差分析。二因素都是固定因素二因素均为随机因素固定模型随机模型混合模型一个因素是固定因素，一个因素是随机因素二因素方差分析三种模型在计算上类似，但在对待检验及结果解释时有所不同。\n主效应和互作主效应（maineffect）：各试验因素的相对独立作用（不同饲料的增重差异，不同品种玉米产量不同）互作、交互（interaction）：某一因素在另一因素的不同水平上所产生的效应不同。\n方差分析的基本假定正态性可加性方差同质性\n二因素方差分析\n六、回归与相关的概念相关变量因果关系平行关系回归分析(regressionanalysis)相关分析(correlationanalysis)一个变量的变化受到另一个变量或几个变量的制约两个以上变量之间共同受到另外因素的影响\n(一)、直线回归的变异来源(x,y)实际值与估计值之差，剩余或残差。估计值与均值之差，它与回归系数的大小有关。\n因变量y的平方和，总平方和，SST或SS总回归平方和U/SSR离回归平方和Q/SSE变异分解\n两个变量是否存在线性关系，采用F检验法进行。也以采用t检验法进行（需分别检验a、b值）。若x与y间不存在直线关系，则总体回归系数β=0;若x与y间存在直线关系，则总体回归系数β≠0.F值较大时，说明方程的变异主要有回归平方和（U）造成，方程成立。t检验法F检验法回归方差离回归方差=F\n直线回归的适应范围一般以自变量的取值为限。直线回归注意问题在自变量范围内求出的估计值，一般称为内插(interpolation);超过自变量取值范围所计算出的估计值，称为外延(extrapolation)。若无充分理由证明超过自变量取值范围还是直线，应该避免外延。\n决定系数coefficientofdetermination变量x引起y变异的回归平方和占y总变异平方和的比率