统计学资料3

统计学资料3

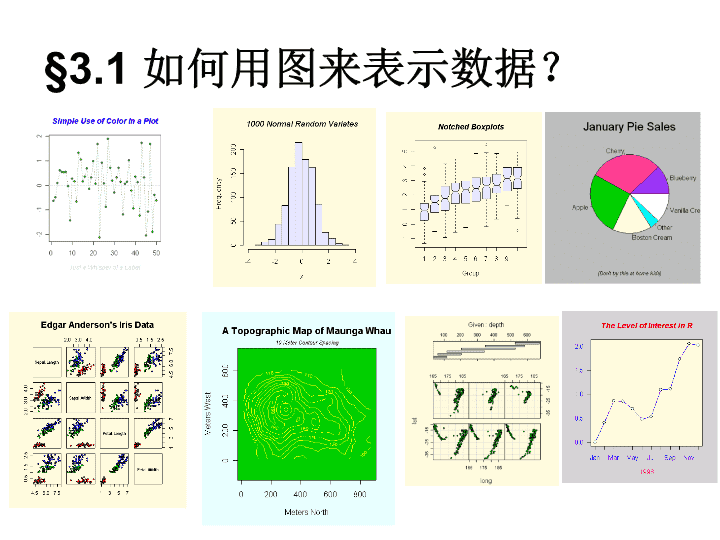
第三章数据的描述\n在对数据进行深入加工之前，总应该对数据有所印象。可以借助于图形和简单的运算，来了解数据的一些特征。由于数据是从总体中产生的，其特征也反映了总体的特征。对数据的描述也是对其总体的一个近似的描述。\n§3.1如何用图来表示数据？\n§3.1.1定量变量的图表示:1.直方图对于一个定量变量，比如某个地区（地区1）测量了163个高三男生的身高（S3height1.txt）。用图形来表示这个数据，使人们能够看出这个数据的大体分布或“形状”的一个办法是画直方图(histogram)。图3.1就是利用这个数据由SPSS软件所画的直方图。\n该图的横坐标是身高区间，这里每一格代表5cm的身高范围（格子宽度因不同的数据性质或要求而定，这里的格子宽度为5cm），而纵坐标为各种身高区间的身高的频数。直方图\n§3.1.1定量变量的图表示:2.盒型图简单一些的是盒形图(boxplot，又称箱图、箱线图、盒子图)。图3.2的左边一个是根据地区1高三男生的身高数据所绘的盒形图；其右边的图代表另一个地区（地区2）的高三学生的身高（height.txt，height.sav，第三章例.xls）。\n盒型图盒子的中间横线是数据的中位数(median)，封闭盒子的上下两横线（边）为上下四分位数（点）；按照SPSS的默认选项，如果所有样本中的数目都在离四分位点1.5倍盒子长度之内，则线的端点为最大和最小值，否则线长就是1.5倍的盒子长度（盒子长度称为四分位间距），在其外面的度量单独点出\n§3.1.1定量变量的图表示:3.茎叶图在直方图和盒形图中，很难恢复数据的原貌。而另一种图：茎叶图(stem-and-leafplots)可以恢复数据以地区1高三男生身高为例（图3.3），茎叶图既展示了分布形状又有原始数据。它象一片带有茎的叶子。茎为较大位数的数字，叶为较小位数的数字。\n茎叶图其中茎叶图中茎的单位为10cm，而叶子单位为1cm。比如，由于第一行茎为150cm，因此叶子中的九个数字001223344代表九个数目150、150、151、152、152、153、153、154、154cm等。每行左边有一个频数（比如第一行有9个数目，第二行有17个等等）；可以看出最长的一行为从165cm到169cm的一段（有35个数）。\n§3.1.1定量变量的图表示:4.散点图数据会有两个变量，如美国男士和女士初婚年限数据（marriage.txt）。该数据描述了自1900年到1998年男女第一次婚姻延续的时间。这里年份是一个变量，婚姻延续时间是第二个变量。由于不可能将所有人的婚姻年限都给出来，所以每年就取了一个中间的值(中位数)作为代表。\n散点图\n§3.1.2定性变量的图表示：饼图定性变量（或属性变量，分类变量）不能点出直方图、散点图或茎叶图，但可以描绘出它们各类的比例。下面用SPSS绘的图3.5（饼图，piechart）表示了说世界各种主要语言人数的比例(language.txt).\n饼图\n§3.1.2定性变量的图表示：条形图而用同样数据画的图3.6称为条形图（barchart）。从每一条可以看出讲各种语言的实际人数，而且分别给出了每个语种中母语和日常使用的人数（在图中并排放置）。条形图显示比例不如饼图直观。\n条形图\n§3.2如何用少量数字来概括数据？大量的数字既繁琐又不直观；需要对数据做人们时间和耐心所允许的简化我们可以用“平均”，“差距”或百分比等来概括大量数字。由于定性变量主要是计数，比较简单，常用的概括就是比例或百分比。下面主要介绍关于定量变量的数字描述。\n§3.2如何用少量数字来概括数据？可用少量所谓汇总统计量或概括统计量(summarystatistic)来描述定量变量的数据。这些数字是从样本数据得来的，因而也是样本的函数，任何样本的函数，只要不包含总体的未知参数，都称为统计量(statistic)。样本的随机性决定统计量的随机性（统计量也是随机变量）\n§3.2如何用少量数字来概括数据？概括统计量经常对应于总体的无法观测到的某些参数。这时，统计量可作为这些参数的估计。一些统计量还可以用来检验样本和假设的总体是否一致。\n§3.2如何用少量数字来概括数据？注：一些统计量前面有时加上“样本”二字，以区别于总体的同名参数。如“样本均值”和“样本标准差”，以区别于总体均值和总体标准差；但在不会混淆时可以只说“均值”和“标准差”。\n§3.2.1数据的“位置”数据有位置吗？这里三个数据的位置一样吗？\n§3.2.1数据的“位置”“位置”一般是关于数据中某变量观测值的“中心位置”或者数据分布的中心（center或centertendency）。和这种“位置”有关的统计量就称为位置统计量(locationstatistic)。位置统计量当然不一定都是描述“中心”了，比如后面要讲的k百分位数（或k％分位数）。\n§3.2.1数据的“位置”最常用的位置统计量就是小学时所学到的算术平均数，它在统计中叫做均值(mean)；严格地说叫做样本均值(samplemean)，以区别于总体均值。如果记样本中的观测值为x1,…,xn，则样本均值定义为\n(样本)中位数(median)是数据按照大小排列之后位于中间的那个数(如果样本量为奇数)，或者中间两个数目的平均(如果样本量为偶数)。由于中位数不易被极端值影响，所以中位数比均值稳健(robust)。§3.2.1数据的“位置”\n上下四分位数（或分别称为第一四分位数和第三四分位数，firstquantile,thirdquantile）则分别位于（按大小排列的）数据的上下四分之一的地方。§3.2.1数据的“位置”\n§3.2.1数据的“位置”一般地还称上四分位数为75百分位数（75pecentile，有75％的观测值小于它），下四分位数为25百分位数（有25％的观测值小于它）。一般地，k百分位数（k-pecentile）意味着有k％的观测值小于它。如果令a=k%，则k百分位数也称为a分位数(a-quantile)。样本中出现最多的数目，称为众数(mode)\n§3.2.2数据的“尺度”这两个数据“胖瘦”一样吗？\n§3.2.2数据的“尺度”数据中数目的分散程度由尺度统计量（scalestatistic）来描述。尺度统计量是描述数据散布，即描述集中与分散程度或变化（spread或variability）的度量。\n§3.2.2数据的“尺度”从前面两个高三男生身高数据的盒形图。左边的数据平均要高些，但右边的数据散布范围要小得多。统计中有许多尺度统计量。一般来说，数据越分散，尺度统计量的值越大。\n§3.2.2数据的“尺度”极差(range)；就是极大值和极小值之间的差。前面两个高三男生身高数据的极差分别为50cm和32cm。盒形图盒子的长度为两个四分位数之差，称为四分位数极差或四分位间距(interquantilerange)；它描述了中间半数观测值的散布情况。极差和四分位极差实际上各自只依赖于两个值，信息量太少。\n§3.2.2数据的“尺度”另一个常用的尺度统计量为（样本）标准差(standarddeviation)。度量样本中各数值到均值距离的一种平均。标准差实际上是方差(variance)的平方根。如果记样本中的观测值为x1,…,xn，则样本方差为\n§3.2.2数据的“尺度”两个均值一样，但右边的要“胖”些，方差为左边的一倍\n§3.2.3数据的标准得分假定两个水平类似的班级（一班和二班）上同一门课，但是由于两个任课老师的评分标准不同，使得两个班成绩的均值和标准差都不一样(数据：grade.txt)。\n§3.2.3数据的标准得分一班分数的均值和标准差分别为78.53和9.43，而二班的均值和标准差分别为70.19和7.00。那么得到90分的一班的张颖是不是比得到82分的二班的刘疏成绩更好呢？怎么比较才能合理呢？\n§3.2.3数据的标准得分虽然这种均值和标准差不同的数据不能够直接比较，但是可以把它们进行标准化，再比较标准化后的数据。一个标准化的方法是把某样本原始观测值（亦称得分，score）和该样本均值之差除以该样本的标准差；得到的度量称为标准得分(standardscore，又称为z-score)。\n§3.2.3数据的标准得分即，某观测值xi的标准得分定义为\n§3.2.3数据的标准得分在我们的例子中，张颖的标准得分为(90-78.53)/9.43＝1.22，而刘疏的标准得分为(82-70.19)/7＝1.69。显然如果两个班级平均水平差不多，刘疏的成绩应该优于张颖的成绩；这是在标准化之前的数据中不易看到的。\n可以看出，原始数据是在各自的均值附近，而散布也不一样。但它们的标准得分则在0周围散布，而且散布也差不多。实际上，任何样本经过这样的标准化后，就都变换成均值为0、方差为1的样本。标准化后不同样本观测值的比较只有相对意义，没有绝对意义。