《管理统计学》PPT课件x

《管理统计学》PPT课件x

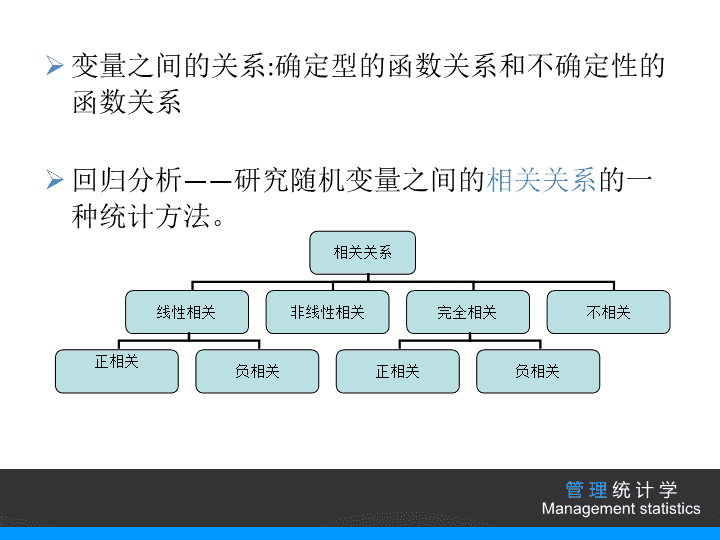
演讲者：xxx第十一章相关与回归分析管理统计学Managementstatistics\n管理统计学Managementstatistics1.变量间的相关关系2.一元线性回归3.多元线性回归4.可线性化的非线性回归目录\n变量之间的关系:确定型的函数关系和不确定性的函数关系回归分析——研究随机变量之间的相关关系的一种统计方法。相关关系线性相关非线性相关完全相关不相关正相关负相关正相关负相关管理统计学Managementstatistics\n相关关系的特点变量间关系不能用函数关系精确表达一个变量的取值不能由另一个变量唯一确定当变量取某个值时，变量的取值可能有几个各观测点分布在直线周围\n不相关正相关负相关相关但无线性关系管理统计学Managementstatistics\n相关系数——对变量之间关系密切程度的度量的取值范围是[-1,1]:完全相关/完全正相关/完全负相关/不存在线性相关关系/负相关/正相关管理统计学Managementstatistics\n对相关系数的显著性检验提出假设:=0计算检验的统计量确定显著性水平，并作出决策若t>拒绝;若t<接受。管理统计学Managementstatistics\n例11.1设有10个厂家的投入和产出如下，根据这些数据，我们可以认为投入和产出之间存在相关性吗？厂家12345678910投入20402030101020202030产出30604060304040503070管理统计学Managementstatistics\n决定系数——说明自变量解释因变量变化百分比的度量。回归分析——一组样本数据出发，确定变量之间的数学关系式，对这些关系式的可信程度进行各种统计检验，并从影响某一特定变量的诸多变量中找出哪些变量的影响显著，哪些不显著。然后利用所求的关系式，根据一个或几个变量的取值来预测或控制另一个特定变量的取值，并给出这种预测或控制的精确程度。管理统计学Managementstatistics\n相关分析与回归分析的区别分析对象的相互地位不同分析对象的变量类型不同两者的目的不同管理统计学Managementstatistics\n一元线性回归的基本概念1一元线性回归（linearregression），只研究一个自变量与一个因变量之间的统计关系。2对于只涉及一个自变量的简单线性回归模型可表示为：3其中，b0和b1称为模型的参数；e是误差项，有4描述y的平均值或期望值如何依赖于x的方程称为回归方程对于一个给定的x值，y的期望值为：\n最小二乘回归法（leastsquaresregression）就是寻找一条直线，使得所有点到该直线的垂直距离的平方和最小。用数据寻找一条直线的过程也叫做拟合一条直线。\n包含残差的散点图Textinhere真实值与预测值的差就是回归直线在每个给定点上的误差，我们称之为残差（residual）。从几何上讲，残差是回归直线到样本数据点之间的垂直距离，确定斜率和截距的方程使回归直线位于样本点之间。这样，从回归直线到样本点之间的垂直距离相互抵消，使总和为0。一元线性回归方程\n残差一般沿着轴显示投入与产出例子中沿轴的残差分布：残差也用来确定异常点（outliers），异常点就是与其他点偏离，与总体趋势不符的数据点。异常点往往使残差幅度加大，在散点图中很容易识别。回归直线方程会受到计算中每个点的影响，因此，异常点的存在可能会使回归直线向异常点偏离。\n回归方程的显著性检验（总体显著性检验）观测值与其平均值的偏差平方和称为总离差平方和。记为SST（totaldeviationsumofsquares）SST来源于两个方面：一是由于自变量x的取值不同造成的；二是除x以外的其他因素(如对的非线性影响、测量误差等)的影响造成的。可分解为两部分：\n总离差平方和反映因变量的个观察值与其均值的总离差DescriptionofthecontentsDescriptionofthecontentsDescriptionofthecontentsDescriptionofthecontents其中称作回归平方和（regressionsumofsquares）,记作SSR；称作残差平方和（residualsumofsquares）,记作SSE。SST=SSR+SSE回归平方和反映自变量的变化对因变量y取值变化的影响残差平方和反映除以外的其他因素对取值的影响，也称为不可解释的平方和或剩余平方和\n回归系数的显著性检验在简单回归（一元回归）中只有一个回归系数需要检验，而回归系数就是回归直线的斜率，所以检验总体显著性的F检验就等价于回归系数的检验。对回归系数的显著性检验就是检验x与y之间是否具有线性关系，或者说，检验自变量x对因变量y的影响是否显著。北京理工大学管理与经济学院学Managementstatistics管理统计学Managementstatistics\n检验步骤如下：提出假设(没有线性关系)(有线性关系)计算检验的t统计量，自由度为n-2；确定显著性水平，并进行决策若拒绝H0；若接受H0。回归系数的显著性检验步骤如下：\n预测标准误差预测标准误差是y的实际值与y的估计推算值离差的一般水平，反映y的预测值对y的实际值的代表性的优劣。预测标准误差的计算公式为：式中：n-2是自由度，Syx是y对x的预测标准误差。北京理工大学管理与经济学院学Managementstatistics管理统计学Managementstatistics\n回归方程在估计和预测中的应用点估计y的平均值的点估计利用估计的回归方程，对于自变量x的一个给定值x0，求出因变量y的平均值的一个估计值就是平均值的点估计。y的个别值的点估计利用估计的回归方程，对于自变量x的一个给定值x0，求出因变量y的一个个别值的估计值就是个别值的点估计。北京理工大学管理与经济学院学Managementstatistics管理统计学Managementstatistics\n区间估计对于自变量的一个给定值x0，根据回归方程得到因变量的一个估计区间。置信区间估计利用估计的回归方程，对于自变量x的一个给定值x0，求出因变量y的平均值的估计区间，这一估计区间称为置信区间。用公式表示在1-a置信水平下的置信区间：北京理工大学管理与经济学院学Managementstatistics管理统计学Managementstatistics回归方程在估计和预测中的应用\n相关系数，决定系数和预测标准误差的三者关系相关系数衡量的是两变量之间相关的强弱程度。当散点图中各点都趋近于回归直线时，相关系数也较大（趋于1）。因此，预测标准误差和相关系数用的是不同的度量方法来表达相同的信息。他们的计算当中都会用到。相关系数的平方是决定系数。决定系数衡量的变量y中有百分之多少能用变量x来解释。北京理工大学管理与经济学院学Managementstatistics管理统计学Managementstatistics\n决定系数r2可以直接从ANOVA中得出。它表示回归平方和占总离差平方和的比例。当SSE或标准误差减小时，r2增加。预测标准误差也可以从ANOVA中得出：北京理工大学管理与经济学院学Managementstatistics管理统计学Managementstatistics\n多元线性回归描述因变量y如何依赖于自变量和误差项的方程称为多元线性回归模型。涉及个自变量的多元线性回归模型可表示为：总体回归参数是未知的，要利用样本数据去估计。用样本统计量代替回归方程中的未知参数,即得到估计的回归方程：北京理工大学管理与经济学院学Managementstatistics管理统计学Managementstatistics\n二元线性回归方程为：其中，分别是的偏回归系数。同理三元线性回归方程为：由样本数据推算、估计回归方程中各个回归系数，是多元回归分析中的一个重要方面，下面简要介绍回归系数的计算方法。北京理工大学管理与经济学院学Managementstatistics管理统计学Managementstatistics\n二元线性回归方程中回归系数可由以下方程组解出：用手解这些方程枯燥而费时，一般来说，自变量超过3个时，要用矩阵运算，可以借助计算机软件解出参数。北京理工大学管理与经济学院学Managementstatistics管理统计学Managementstatistics\n对多元回归模型的评估如果检验水平合适而且数据足够多，用多元回归模型几乎可以处理所有数据组。模型一旦建立，一件很重要的事就是检验模型与数据是否很好拟合以及与回归分析的假设前提是否相符。检验回归模型是否恰当的方法有很多，如：检验模型整体的显著性、检验回归系数的显著性、计算残差、检验样本决定系数等。北京理工大学管理与经济学院学Managementstatistics管理统计学Managementstatistics\n模型的整体检验对多元回归方程的整体性检验，就是要看自变量是否整体上对随机变量y有影响。检验方法是将回归离差平方和(SSR)同残差平方和(SSE)加以比较，应用F检验来分析二者之间的差别是否显著。如果是显著的，因变量与自变量之间存在线性关系；如果不显著，则因变量与自变量之间不存在线性关系。北京理工大学管理与经济学院学Managementstatistics管理统计学Managementstatistics\n多元回归模型的整体性检验的步骤如下：提出假设H0:H1:至少有一个回归系数不等于0。计算检验统计量F回归平方和；残差平方和确定显著性水平和分子自由度m,分母自由度n-m-1,找出临界值Fa；作出决策：若FFa，拒绝H0；若F

查看更多