- 2022-09-01 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
统计学实验设计
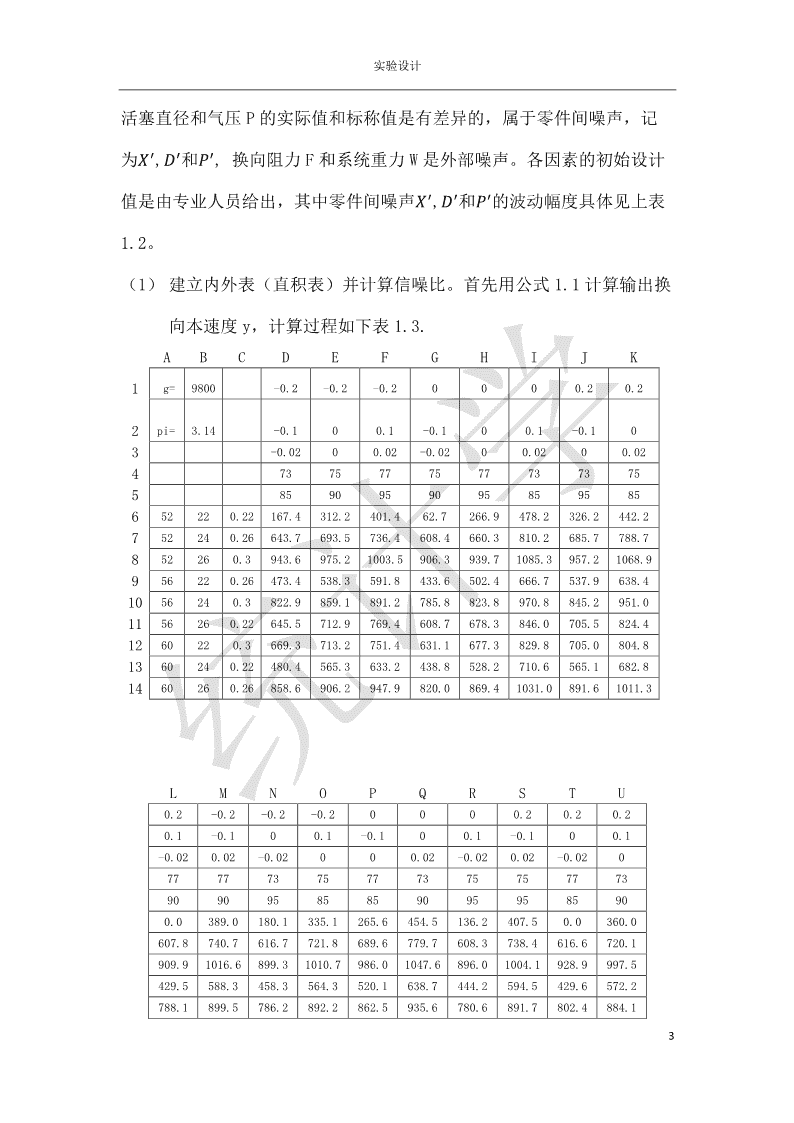
实验设计稳健性设计题目:分别用内外表稳健型设计和综合噪声法稳健设计寻找因素间的最优搭配。姓名:樊海涛专业:统计学学号:12070601061\n在一项关于活塞气动换向实验的研究中,实验指标是换向本速度y,其目标值是960mm/s。影响实验指标的3个可控因素是换向行程2X(mm),活塞直径D(mm),气缸气压P(kgf/mm);影响实验指标的3个外噪音因素是换向阻力F(kgf),系统重力W(kg),实验指标y与6个影响因素的关系是:11y=√Xg(D2P−2F)(mm/s)(图1)W22其中g=9800mm/s是重力加速度,π=3.142是圆周率。如果根号内的数值为负数时则取y=0。因素与噪声水平如下表:表1.2水平123可X525660控D222426因素P0.220.260.3X’X-0.2XX+0.2噪D’D-0.1DD+0.1声P’P-0.02PP+0.02因素F737577W859095(一)用内外表稳健性设计方法寻找符合要求的稳健搭配,其中内表417使用L9(3)正交表的前三列,外表使用L18(2*3)的第2~6列。解这个问题是可计算项目,共5个影响因素,换向行程X,活塞直径和气压P是可控因素,换向阻力F和系统重力W是不可控因素,换向行程X,\n实验设计活塞直径和气压P的实际值和标称值是有差异的,属于零件间噪声,记为?′,?′和?′,换向阻力F和系统重力W是外部噪声。各因素的初始设计值是由专业人员给出,其中零件间噪声?′,?′和?′的波动幅度具体见上表1.2。(1)建立内外表(直积表)并计算信噪比。首先用公式1.1计算输出换向本速度y,计算过程如下表1.3.ABCDEFGHIJK1g=9800-0.2-0.2-0.20000.20.22pi=3.14-0.100.1-0.100.1-0.103-0.0200.02-0.0200.0200.024737577757773737558590959095859585652220.22167.4312.2401.462.7266.9478.2326.2442.2752240.26643.7693.5736.4608.4660.3810.2685.7788.7852260.3943.6975.21003.5906.3939.71085.3957.21068.9956220.26473.4538.3591.8433.6502.4666.7537.9638.41056240.3822.9859.1891.2785.8823.8970.8845.2951.01156260.22645.5712.9769.4608.7678.3846.0705.5824.41260220.3669.3713.2751.4631.1677.3829.8705.0804.81360240.22480.4565.3633.2438.8528.2710.6565.1682.81460260.26858.6906.2947.9820.0869.41031.0891.61011.3LMNOPQRSTU0.2-0.2-0.2-0.20000.20.20.20.1-0.100.1-0.100.1-0.100.1-0.020.02-0.02000.02-0.020.02-0.02077777375777375757773909095858590959585900.0389.0180.1335.1265.6454.5136.2407.50.0360.0607.8740.7616.7721.8689.6779.7608.3738.4616.6720.1909.91016.6899.31010.7986.01047.6896.01004.1928.9997.5429.5588.3458.3564.3520.1638.7444.2594.5429.6572.2788.1899.5786.2892.2862.5935.6780.6891.7802.4884.13\n实验设计606.1775.3618.2741.4708.9814.8608.2772.5615.1739.8631.5753.1642.4743.5705.9797.4633.5752.2639.4742.9432.2632.1464.5591.5548.1681.9448.4637.1432.7599.0821.1958.4819.5940.3911.1994.4813.2949.2836.8931.1在表1.3,按照表所示的格式输入数据,在D6单元格内输入公式:=IF((($A6+D$1)*$B$1*(0.5*$B$2*($B6+D$2)^2*($C6+D$3)-2*D$4)/D$5)<0,0,SQRT(($A6+D$1)*$B$1*(0.5*$B$2*($B6+D$2)^2*($C6+D$3)-2*D$4)/D$5)),再把公式复制到“D7:V15”中,就得到1.3中所示的换向本速度y的计算结果,然后再对每个内表实验计算出信噪比计算结果如下图1.4yi均值ViXDPSNR52220.22…276.9622173.415.2552240.26…692.594167.9920.6152260.3…976.463173.2424.7856220.26…534.575688.1717.0056240.3…859.603339.0023.4556260.22…710.616118.2519.1660220.3…712.433832.3821.2260240.22…559.568220.4315.8060260.26…906.174556.2622.56(2)稳健设计。找出最稳健的因素水平搭配,从表1.4可以看到,内表的第三组搭配X=52,D=26,P=0.3的信噪比SNR=24.78最大,得直接看到的最稳健的因素水平搭配是X1D3P3,但这组搭配输出换向本速度976.46,比目标值960,大了16.46,这时需要在换向行程X,活塞直径D和气压P中找到一个调节因素,这个调节因素对信噪比SNR不敏感,而对电流强度y敏感,为止继续下面的工作。4\n实验设计(3)找出对信噪比SNR不敏感的因素。以信噪比为响应因素。以信噪比为响应因素做方差分析,得到方差分析表1.5如下,这个表同时列出了因素在各个水平下信噪比的平均值。下图1.6实验号XDPSNR11115.25212220.61313324.78421217.00522323.45623119.16731321.22832115.80933222.56通过spss做因素方差分析,结果如下图1.7;主体间效应的检验因变量:信噪比SNRIII型平方源和df均方FSig.a校正模型260.332643.3895.340.166截距3204.69213204.692394.441.003X17.82128.9101.097.477D93.678246.8395.765.148P148.833274.4179.159.098误差16.24928.125总计3481.2739校正的总计276.5818a.R方=.941(调整R方=.765)从图1.7中看到,换向行程X,活塞直径D和气压P的sig(P值)都大于0.05,对信噪比都没有显著影响;其中X的P=0.477是最大值,可能是它的存在影响其它因素的显著性,所以剔除换向行程X后再做一次方差5\n实验设计分析,结果如表1.8所示主体间效应的检验因变量:信噪比SNRIII型平方源和df均方FSig.a校正模型242.511460.6287.118.042截距3204.69213204.692376.249.000D93.678246.8395.499.071P148.833274.4178.737.035误差34.07048.517总计3481.2739校正的总计276.5818a.R方=.877(调整R方=.754)在剔除换向行程X后,调整R方变化很小,仅减小0.011,对模型的整体拟合效果没有太大的影响,但气压P从原来的不显著变成显著水平,是信噪比的敏感因素,活塞直径D值虽然减小了,但是依旧不显著,是信噪比的不敏感因素。从上面可以得到综合比较法最稳健的搭配,在P因素的3个水平中,3水平的信噪比最大为23.15,D因素3水平中,3水平的信噪比最大为22.16,D也是信噪比的不敏感因素,从实际考虑D也可以选择一些其他值,X因素的3个水平中2水平为信噪比为19.87,3水平信噪比19.86,这两个水平相差甚微,应该从成本,效率,安全的角度考虑去选择,为了可继续性,本文就随便选择2水平,所以最稳健的因素搭配是X2D3P3,这个搭配最关键的是P要选择3水平,因为它是信噪比的敏感因素,XD可以有专业人员解释实际与理论进行选择。(4)灵敏度设计。由于换向行程X活塞直径D都是信噪比的不敏感因6\n实验设计素,如果它对换向本速度y有显著影响,就可以作为调节因素,为此以內表每个处理下换向本速度的平均值yi为响应变量做方差分析,得方差分析表如下1.9所示。主体间效应的检验因变量:平均值yi源III型平方和df均方FSig.a校正模型369320.633661553.439136.462.007截距4311090.90014311090.9009557.557.000X9387.35124693.67610.406.088D191187.714295593.857211.929.005P168745.568284372.784187.052.005误差902.1322451.066总计4681313.6669校正的总计370222.7658a.R方=.998(调整R方=.990)从表1.9可知,R方为0.990,说明模型整体拟合效果非常高,但换向行程依然不显著,所以可知X对信噪比跟换向本速度都不显著,都不敏感因,所以X对稳健性和目标值都没大的影响,所以在实验时可以剔除不与考虑,但上表中有一个亮点就是D的sig(P值)=0.005<0.05,是影响换向本速度y的显著因素,但是D在对信噪比时又是不显著的因素,因此可以确定活塞直径D是这个实验的调节因素。(5)实验验证由于换向本速度y是活塞直径D的增函数,所以要把活塞直径的取值进一步减小,取X=52,D=25.56,P=0.30时y=960.6,;X=52,D=25.55P=0.30时y=959.8且信噪比几乎没有什么变化,这两个y值都与目标值y=960非常接近,这种做法整体上还是很让人满意的。这也完全符合田口玄一博士的稳健性思想。7\n实验设计4(二)用综合噪声法作稳健性设计,使用L9(3)正交表安排X,D,P这3个因素,其中:N1条件为:X-0.2,D-0.1,P-0.02和F3,W3N2条件为:X+0.2,D+0.1,P+0.02和F1,W1用内外表方法做稳健型设计时总试验次数是内外表试验次数的乘积,因而需要大量的试验次数,这是它的一个主要缺点,这个缺点严重影响了它的适用范围,通常只是针对可计算项目才使用这种方法。在必须通过实验才能得到实验结果而又不能承担试验费用的情况下,可以采用综合噪声法进行稳健性设计。定义:不管有多少个噪声因素,也不管每个噪声因素有多少个水平,把这些噪声因素综合成一个2水平的综合噪声因素的方法,称为综合噪声法。这个综合噪声因素记作N。综合噪声的两个水平分别为:N1:负侧最坏水平,是使产品性能指标达到最小值的各噪声因素水平的组合。N2:正侧最坏水平,是使产品性能指标达到最大值的各噪声因素水平的组合。零件间噪声水平是由3个可控因素的水平分别加减一个误差常数产生4的,选用L9(3)正交表安排內表实验,为了减少实验的次数,采用综合噪声实验方法,噪声因素各取两个水平,然后将噪声因素综合为换向本速度最小条件N1和换向本速度最大条件N2这两种情况。如下表1.10.8\n实验设计ABCDEFGH1g=9800-0.20.22pi=3.142-0.10.13-0.020.02yi均值ViSNR4737558590652220.22167.4440.6304.037306.93.0752240.26643.7774.3709.08538.317.7852260.3943.61045.9994.75237.322.8956220.26473.4629.9551.712252.713.91056240.3822.9932.1877.55963.921.11156260.22645.5808.6727.113299.315.91260220.3669.3791.3730.37449.318.51360240.22480.4672.5576.418445.912.41460260.26858.6990.4924.58692.019.9(2)稳健设计,找出最稳健的因素水平搭配,从表1.10可以看出,内表的第三组搭配信噪比SNR=22.8最大,是最稳健的因素水平搭配,其水平搭配是X1D3P3.下表1.11列出了各因素水平信噪比的平均值与上述实验的得到搭配X因素不同,D,P均相同。XDP水平114.4611.7810.44水平216.9617.0617.14水平316.9519.5320.79(2)分析因素对信噪比SNR的敏感性。采用方差分析,以信噪比作为响应变量作方差分析;下图1.129\n主体间效应的检验因变量:信噪比SNRIII型平方源和df均方FSig.a校正模型271.670645.2787.979.116截距2339.65712339.657412.301.002X12.50026.2501.101.476D94.042247.0218.286.108P165.128282.56414.550.064误差11.34925.675总计2622.6769校正的总计283.0198a.R方=.960(调整R方=.840)从表1.12看出,所有因素的P值都大于0.05,这是先剔除一个最不显著的因素X,再做方差分析,如下图1.13.主体间效应的检验因变量:信噪比SNRIII型平方源和df均方FSig.a校正模型259.170464.79210.867.020截距2339.65712339.657392.403.000D94.042247.0217.886.041P165.128282.56413.847.016误差23.85045.962总计2622.6769校正的总计283.0198a.R方=.916(调整R方=.831)得可控因素D和P的p值分别为0.041和0.016,是对信噪比有显著影响的因素,因而X是信噪比不敏感的因素。\n实验设计下图1.14g=9800-0.20.2pi=3.142-0.10.1-0.020.02yi均值ViSNR7377859552220.22167.4402.9285.227732.13.952240.26643.7739.2691.54569.420.252260.3943.61007.4975.52036.226.756220.26473.4593.9533.67263.615.956240.3822.9894.4858.72554.824.656260.22645.5772.2708.88020.317.960220.3669.3753.9711.63583.321.560240.22480.4635.3557.811993.514.160260.26858.6951.1904.84274.522.8哎综合噪声法中,忘了把F,W分别取最小值,最大值,所以上述方法跟正确做法数据有出入,但方法是对的,我就不重负做了,正确数据如上表。有时间继续研究。11查看更多