- 2022-09-01 发布 |
- 37.5 KB |
- 21页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
统计学实验报告
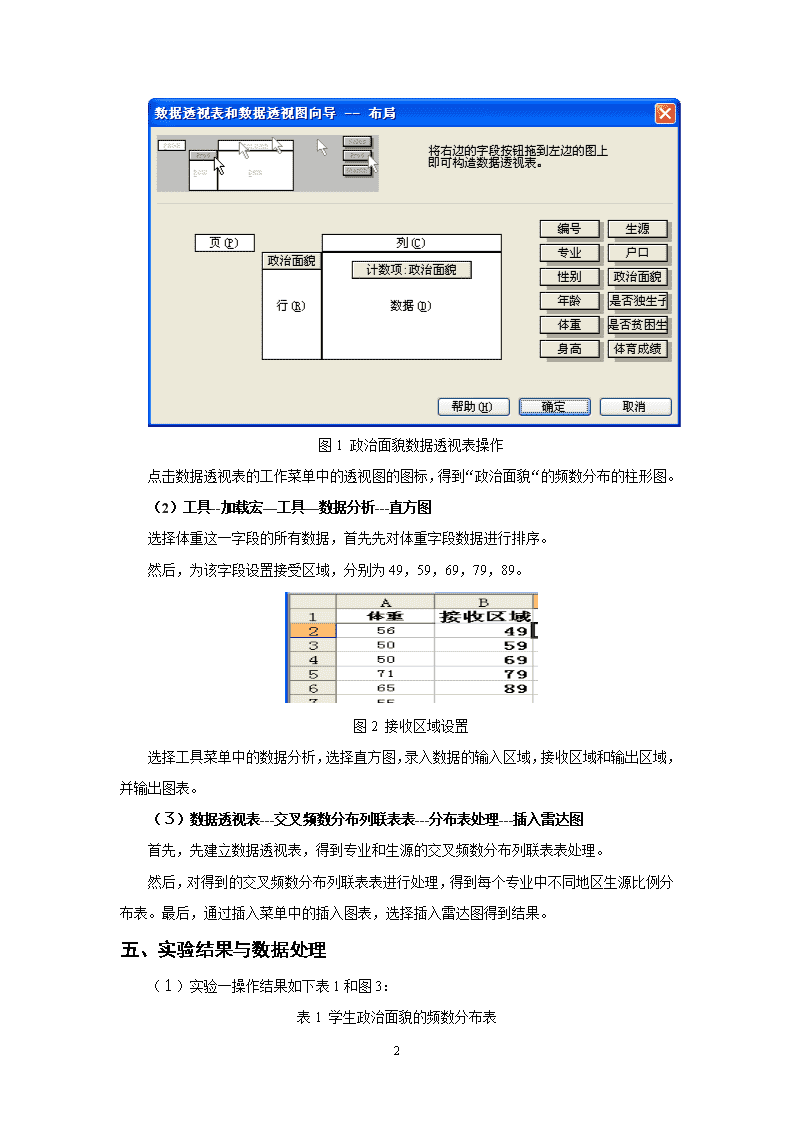
福建农林大学经济与管理学院旅游学院实验报告课程名称:统计学专业班级:学号:学生姓名:指导教师:成绩:2011年12月20日5\n实验一:EXCEL的数据整理与显示一、实验目的及要求:(一)目的1.了解EXCEL的基本命令与操作、熟悉EXCEL数据输入、输出与编辑方法;2.熟悉EXCEL用于预处理的基本菜单操作及命令;3.熟悉EXCEL用于整理与显示的基本菜单操作及命令。(二)内容及要求根据学生实验数据2011-2012,1.用Excel制作一张学生政治面貌的频数分布表,并绘制一张柱状图,反映不同政治面貌的学生人数分布情况。2.对学生的体重进行等距分组,整理成频数分布表,并绘制直方图。3.编制生源与专业交叉分布的列联表,并画出雷达图,比较两个专业的学生生源的分布是否相似。二、仪器用具硬件:计算机(安装Windows98、Windows2000或WindowsXP或以上)软件:EXCEL三、实验原理统计中数据整理与显示的相关理论。四、实验方法与步骤(1)选中所有的数据—数据—数据透视表和数据透视图打开数据表,选中所提供的所有数据。点击“数据”,选择“数据透视表和数据透视图”,进入数据透视表和数据透视图向导页面,选择数据区域—布局—将“政治面貌”字段拉入“行”区域,在“数据“中拉入”政治面貌“,选择其汇总方式为“计数”,见图1,将结果保持在新工作表中,得到学生政治面貌的频数分布表。5\n图1政治面貌数据透视表操作点击数据透视表的工作菜单中的透视图的图标,得到“政治面貌“的频数分布的柱形图。(2)工具--加载宏—工具—数据分析---直方图选择体重这一字段的所有数据,首先先对体重字段数据进行排序。然后,为该字段设置接受区域,分别为49,59,69,79,89。图2接收区域设置选择工具菜单中的数据分析,选择直方图,录入数据的输入区域,接收区域和输出区域,并输出图表。(3)数据透视表---交叉频数分布列联表表---分布表处理---插入雷达图首先,先建立数据透视表,得到专业和生源的交叉频数分布列联表表处理。然后,对得到的交叉频数分布列联表表进行处理,得到每个专业中不同地区生源比例分布表。最后,通过插入菜单中的插入图表,选择插入雷达图得到结果。五、实验结果与数据处理(1)实验一操作结果如下表1和图3:表1学生政治面貌的频数分布表5\n政治面貌汇总共青团员160其他7中共党员13总计180图3学生政治面貌的频数分布柱状图(2)实验二操作结果如下表2、和图4:表2接收区域结果输出接收区域频率累积%40-495832.22%50-597071.11%60-694093.33%70-791199.44%80-891100.00%其他0100.00%图4 学生体重频率分布直方图5\n(3)实验三操作结果如下表3、表4和图5:表3生源与专业交叉分布的列联表专业生源北京、天津、上海农村省会城市县城小城镇、集镇中等城市总计会计251314231223110物流1412131451270总计392527371735180表4生源与专业交叉分布的列联表数据处理生源专业会计物流北京、天津、上海0.22730.2农村0.11820.1714省会城市0.12730.1857县城0.20910.2小城镇、集镇0.10910.0714中等城市0.20910.1714总计11图5生源与专业交叉分布雷达图六、讨论与结论对于实验一,我比较常用的是数据透视表和数据透视图。关于这数据透视表和数据透视图,刚开始应用的时候,比较生疏。其实,在学校统计学之前,我们已经接触过这数据透视表和数据透视图了。但是,由于使用不经常,导致对其掌握不够。在今年学习统计学后,对于透视表中行和列的数据选择方面就比较不清楚该把哪个因素放在行向量,哪个应该放在列向量。5\n第二个实验题目,对于我来说,就比较陌生了。如果没有认真地在课上,听老师的讲解,我就不知道如何下手了。这关于接收区域,这是以前从来就没有接触过的。还好,我认真听课了,虽然,操作地不是很流畅。但是,大概的步骤就比较清楚。而后面,为了视图的美观,我们又要修改接收区域。其实,在excel所输出的操作结果里,“人数”这一栏系统总是默认为“频率”。但是,其实这一项是频数。操作时如果不注意,我们就会被误导了。对于第三题中的雷达图,我之前也没有自己操作过。这操作过程中,我原先是没有进行我所描写的步骤里的第二步的。就是说没有对得到的交叉列联表进行处理。只是单纯的利用输出的数量进行画图。但是,总会出现错误。后来,老师告诉我,这雷达图画图使用的数据必须是百分比数据。这才把这一题给解决了。其实,这统计学学习还挺有趣的。因为这一门课程,我才发觉自己对excel的利用是非常不够的。生活中其实很多地方都可以直接利用excel的强大功能了。5\n实验报告评分表学生姓名念彩娟学号091735013专业年级2009旅游管理实验项目名称实验一:EXCEL的数据整理与显示实验学时3学时评价项目权重评价内容评价结果得分ABCD实验态度20%实验态度端正,遵守实验室守则,严格按照实验要求进行操作。20161412实验过程30%实验项目符合大纲,实验方法科学;步骤操作合理,逻辑条理清晰,符合指导书要求。30242118实验结论与讨论30%实验结论正确,分析、讨论深入。30242118实验报告描述20%语言精炼、流畅、准确、灵活,逻辑性强;结构严谨规范,条理清晰,布局合理,系统严密。20161412总分教师签名5\n实验二:EXCEL的数据特征描述、列联分析、多元回归分析一、实验目的及要求:(一)目的熟悉EXCEL用于数据描述统计、列联分析、多元回归的基本菜单操作及命令。(二)内容及要求根据学生实验数据2011-2012,1.对学生的身高进行描述统计,说明学生身高的一些基本特征。2.对不同户口中贫困生的分布情况编制列联表,并分析贫困生的数量的多少是否与户口的不同是有关。3.根据学生的体育成绩(y1)与学生的年龄(x1)、体重(x2)和身高(x3),性别(x4)建立一个多元回归模型,并判断此模型有无意义。二、仪器用具硬件:计算机(安装Windows98、Windows2000或WindowsXP或以上)软件:EXCEL三、实验原理统计中数据整理与显示的相关理论。四、实验方法与步骤(1)加载宏—分析数据库—工具—数据分析—描述统计—录入数据—得到结果—进行分析首先,先通过工具菜单,选择“加载宏”,选择“分析工具库”。再通过工具中出现的“数据分析”中的“描述统计”,录入输入区域为所有“身高”字段的数据,默认分组方式为“逐列”,选择输出区域,默认系统的其他选项,选择确定后,得到身高特征描述统计表。5\n图1描述统计页面图2身高数据的众数、中位数和平均数及其构成趋势图由描述统计结果及图2可以分析得到:a、由集中趋势度量值中位数、众数和平均值的关系:平均值>中位数>众数,且其偏度为0.248125331>0,故身高因素呈右偏分布;b、由标准差与平均值的比值得到离散系数为0.048458,说明身高变量的离散程度小。c、有峰态度量峰度=-0.696982464可知,身高因素呈平峰分布。(2)数据透视表—布局—列联表—计算得到期望系数—计算期望值—引入统计函数“CHITEST”—对结果进行分析首先,通过“数据”菜单中的透视表和透视图得到贫困生与户口的交叉列联表。5\n由得到的交叉列联表中的数据得到城市户口的期望系数和农村的期望系数。并由此计算得到相应的期望值,得到观察值和期望值对比分布表。表1观察值和期望值对比分布列联表户口贫困生非贫困生贫困生城市户口观察值12214期望值119.3816.62农村户口观察值368期望值38.625.38总计15822将观察值和期望值列表,通过插入统计函数“CHITEST”计算得到p值为0.587505>0.1,因此可以认定贫困生的数量的多少与户口的不同无关。(3)按顺序提取因素—对体育成绩变量的数据进行处理—处理定性数据性别变量—数据分析—回归—分析结果并得到回归方程模型—判断模型有效性首先,将学生的体育成绩(y1)与学生的年龄(x1)、体重(x2)和身高(x3)按顺序提取放在新的工作表中。考虑到,男女生体育成绩不具可比性,先对体育成绩进行处理。先对数据进行“筛选”,选出性别为“女”的学生的所有体育成绩,利用函数公式,将其成绩分别除以0.8,得到结果。然后,用同样步骤选出性别“男”的体育成绩,分别除以1得到结果。又考虑到性别因素是定性因素,对该因素引入0-1变量,以0代表性别为“男”,1代表性别为“女”。然后,通过数据分析中的回归,录入x值和y值,选定适当输出区域,得到计算结果如下表2、表3和表4。表2回归统计结果项目数据结果MultipleR0.796934RSquare0.635103AdjustedRSquare0.626763标准误差25.01996观测值180表3方差分析结果 dfSSMSFSignificanceF回归分析4190671.347667.8376.146872.77007E-37残差175109549.7625.9985总计179300221 5\n表4T检验结果 Coefficients标准误差tStatP-valueLower95%Upper95%Intercept461.0678.625.860.00305.90616.23年龄-1.672.05-0.810.42-5.712.37体重0.310.340.900.37-0.360.98身高-0.920.43-2.150.03-1.76-0.08性别-56.936.20-9.180.00-69.17-44.69最后,对结果进行分析,由回归建立回归方程,我们可得到回归函数模型如下:,并通过回归分析中的、方差分析的分析<0.05和T检验的P值结果,综合判断模型的有效性。五、实验结果与数据处理(1)实验一操作结果如下表5:表5身高特征描述统计项目数据项目数据平均164.7722222区域36标准误差0.595129756最小值150中位数163.5最大值186众数155求和29659标准差7.984503536观测数180方差63.75229671最大(1)186峰度-0.696982464最小(1)150偏度0.248125331置信度(95.0%)1.174372756(2)实验二操作结果如下表2:表6贫困生与户口列联表户口贫困生总计非贫困生贫困生城市12214136农村36844总计(人)15822180将观察值和期望值列表,通过插入统计函数“CHITEST”计算得到p值为0.587505>0.1,因此可以认定贫困生的数量的多少与户口的不同无关。(3)实验三操作结果。由回归得到结果,我们可得到回归函数模型如下:5\n由和修正后的可知,该回归方程能解释体育成绩与三个因素的关系的比率分别0.635103和0.626763,说明该模型可行。查看方差分析结果,其<0.05,该结果是可接受的。查看T检验,发现四个因素中,年龄、体重两个因素不能通过T检验。因此,认为该模型是没有意义的。六、讨论与结论其实,对于这一份实验报告内的内容,因为之前经常应用,总体上我掌握的比较好。我认为,对于这个实验报告,比较有必要提的就是对数据分析工具的应用了。因为,掌握了数据分析工具,很多问题都可以应用这一工具解决的。这一份实验报告中,除了要掌握数据分析工具外,还要具备一定的知识。像我们必须了解这工具处理输出的结果中的数据都分别代表什么意思。比如,我们做回归拟合与预测,我们必须要懂得输出的回归统计表格中的R-Squre是用百分比数据代表我们平时用来表示该拟合的方程模型能够解释数据的程度。如果比值越大,则表示该模型越能够解释数据;否则,反之。还有,方差分析表格中,我们其实需要看的最重要的一个数据,便是significanceF这个项了。这一项就是方差分析中的P值了。如果其值大于0.1,则表示该回归模型不能通过方差检验。而如果其比值小于0.05,则可以认为该模型十分有意义;否则,就可以认为该模型没有意义。同样,在T检验中,我们要注意的就是P-value这个选项了。这个选项的应用标准和方差分析中significanceF的应用标准是一样的。不论在T检验中,有几项没有通过经检,都认为模型不具有存在意义。当然,在T检验中,除了要注意P-value这个选项外,还要注意Coefficients这个选项了。因为,我们所需要的回归方程就是从这而来了。Intercept这一栏中的数据,就是线性回归模型中的常数项了,以下的项就根据不同因素,代表各个自变量的系数。只有掌握了该具备的知识,对于系统输出的结果才能看得懂其意思。否则,即使学会了机械的操作,也无济于事。5\n实验报告评分表学生姓名念彩娟学号091735013专业年级2009旅游管理实验项目名称实验二:用EXCEL展示数据的分布特征、列联分析、多元回归实验学时3学时评价项目权重评价内容评价结果得分ABCD实验态度20%实验态度端正,遵守实验室守则,严格按照实验要求进行操作。20161412实验过程30%实验项目符合大纲,实验方法科学;步骤操作合理,逻辑条理清晰,符合指导书要求。30242118实验结论与讨论30%实验结论正确,分析、讨论深入。30242118实验报告描述20%语言精炼、流畅、准确、灵活,逻辑性强;结构严谨规范,条理清晰,布局合理,系统严密。20161412总分教师签名5\n实验三:时间序列分析一、实验目的及要求:(一)目的掌握EXCEL用于移动平均、线性趋势分析的基本菜单操作及命令。(二)内容及要求综合运用统计学时间序列中的移动平均、季节指数运算、时间序列因素分解、图形展示等知识,并结合经济学等方面的知识,对一家大型百货公司最近几年各季度的销售额数据(见Book13)的构成要素进行分解,并绘制图形进行分析。二、仪器用具硬件:计算机(安装Windows98、Windows2000或WindowsXP或以上)软件:EXCEL三、实验原理时间序列分析中的移动平均分析原理、季节指数原理等。四、实确定验方法与步骤(1)首先,先将数据进行处理,按顺序整理成按季度为单位发展的时间序列。然后,通过移动平均剔除法,采用“4步移动,2步移正”求出该百货公司各季度销售额的中心化移动平均值,并得到销售额与中心化移动平均值的比值。表1某百货公司销售额的中心化移动平均值及其比值年/季时间标号t销售额Y移动平均值中心化移动平均值(CMA)比值(Y/CMA)1991/11993.1——————22971.2——————332264.11542.9251627.9881.390735441943.31713.051833.0881.0601241992/151673.61953.1252161.0880.774425261931.52369.052511.0880.769189373927.82653.1252736.7251.435219483079.62820.3252897.9631.0626781993/192342.42975.62953.0630.793212102552.62930.5253104.6750.8221793113747.53278.8253392.8251.1045374124472.83506.8253718.41.2028837\n续表1某百货公司销售额的中心化移动平均值及其比值年/季时间标号t销售额Y移动平均值中心化移动平均值(CMA)比值(Y/CMA)2144245.24480.8754718.4130.8997093155951.14955.955037.1751.1814364166373.15118.45225.9881.2195021995/1173904.25333.5755496.2630.7103372185105.95658.955941.1250.8594163197252.66223.36420.6751.129574208630.56618.056729.4751.2824921996/1215483.26840.97031.3380.7798232225997.37221.7757233.0380.8291543238776.17244.37199.351.2190134248720.67154.47161.1131.2177721997/1255123.67167.8257269.8380.70477522660517371.857324.4250.826143279592.272777254.351.3222694288341.27231.77328.5131.1381851998/1294942.47425.3257338.8130.673462306825.57252.37300.0380.9349953318900.17347.7757356.2131.2098754328723.17364.657293.71.1959771999/1335009.97222.757112.3380.7043962346257.97001.9256894.7380.9076343358016.86787.556918.7251.1587114367865.67049.96995.1251.124442000/1376059.36940.356908.10.877132385819.76875.856908.6750.8423763397758.86941.5————4408128.25426.675————接着,将得到的比值再按季度进行重新排列,计算出各比值的平均值与季节指数并对数据进行重新整理得到下表2。表2各季节指数计算表年份季度12341991————1.3907354941.0601239719920.77442490.769191.4352191031.0626776619930.79321040.822181.104536781.2028829619940.77385760.899711.1814360231.2195015819950.71033730.859421.129569711.2824923219960.77982320.829151.2190128281.2177716819970.7047750.826141.3222687081.1381845919980.67346050.9351.2098753261.1959773519990.70439570.907631.1587106011.1244402420000.87712970.84238————7\n续表2各季节指数计算表合计6.79141437.6907911.1513645710.5040523平均0.75460160.854531.2390405081.16711693季节指数0.75172780.851281.2343218361.16267216总平均值9.034406——————最后,利用得到的季节指数,插入折线图,得到销售额的季节变动图。(2)通过公式计算得到季节分离后的序列值。然后,利用“数据分析”中的回归工具,建立线性回归,得到回归趋势值如表3,并对模型进行统计检验如表4、表5和表6。表31991—2000年各季度销售额的预测值年/季时间标号销售额(Y)季节指数(S)季节分离后的时间序列(Y/S)回归后的趋势(T)最终预测值预测误差1991/11993.10.7517281321.092207.0981659.137-666.03722971.20.8512781140.8732370.8052018.214-1047.01332264.11.2343221834.2872534.5113128.402-864.302441943.31.1626721671.4082698.2173137.142-1193.841992/151673.60.7517282226.3382861.9242151.388-477.788261931.50.8512782268.9413025.632575.653-644.153373927.81.2343223182.1523189.3373936.668-8.86798483079.61.1626722648.7263353.0433898.49-818.891993/192342.40.7517283116.0213516.752643.639-301.2392102552.60.8512782998.553680.4563133.092-580.4923113747.51.2343223036.083844.1624744.934-997.4344124472.81.16267238474007.8694659.838-187.0381994/1133254.40.7517284329.2274171.5753135.889118.51082144245.20.8512784986.8544335.2823690.531554.66923155951.11.2343224821.3524498.9885553.199397.90064166373.11.1626725481.4254662.6955421.185951.91481995/1173904.20.7517285193.6354826.4013628.14276.06012185105.90.8512785997.9224990.1074247.97857.93043197252.61.2343225875.7775153.8146361.465891.1354208630.51.1626727422.9875317.526182.5332447.9671996/1215483.20.7517287294.1295481.2274120.3911362.8092225997.30.8512787045.0535644.9334805.4081191.8923238776.11.2343227110.0585808.647169.7311606.3694248720.61.1626727500.4815972.3466943.8811776.7191997/1255123.60.7517286815.7656136.0524612.641510.958622660510.8512787108.1356299.7595362.847688.15277\n续表31991—2000年各季度销售额的预测值3279592.21.2343227771.2316463.4657977.9961614.2044288341.21.1626727174.1636627.1727705.228635.97191998/1294942.40.7517286574.726790.8785104.892-162.4922306825.50.8512788017.9436954.5855920.286905.21383318900.11.2343227210.5187118.2918786.262113.83794328723.11.1626727502.6317281.9978466.576256.52421999/1335009.90.7517286664.5137445.7045597.143-587.2432346257.90.8512787351.1817609.416477.725-219.8253358016.81.2343226494.9037773.1179594.528-1577.734367865.61.1626726765.1067936.8239227.923-1362.322000/1376059.30.7517288060.4978100.536089.393-30.09352385819.70.8512786836.4268264.2367035.164-1215.463397758.81.2343226285.8818427.94310402.79-2643.994408128.21.1626726990.9658591.6499989.271-1861.07表4回归统计结果项目数据MultipleR0.882769RSquare0.779281AdjustedRSquare0.773473标准误差1031.834观测值40表5方差分析结果 dfSSMSFSignificanceF回归分析11.43E+081.43E+08134.1654.93E-14残差38404578871064681总计391.83E+08 表6T检验结果 Coefficients标准误差tStatP-valueLower95%Upper95%下限95.0%上限95.0%Intercept2043.39332.516.150.001370.262716.521370.262716.52XVariable1163.7114.1311.580.00135.09192.32135.09192.32由以上表格结果可得到线性回归方程:y=163.71x+2043.4,且模型通过了方差分析检验和T检验,所以该模型有意义。(3)利用季节指数与回归趋势值的乘积,得到含有季节性预测的最终预测值。应用各期实际销售额、季节分离后的销售额、季节分离后的趋势值这三个变量,插入折线图,得到三者的对比情况。(4)通过题(2)中得到的线性回归方程模型,对2001年的各季度的销售额进行预测。五、实验结果与数据处理7\n(1)实验一操作过程如下:表7季节指数分布季节指数10.75172820.85127831.23432241.162672图1某百货公司销售额的季节变动图(2)实验二操作入下:图2销售额的线性趋势预测图7\n(3)实验三操作如下:图3销售额季节分离后的序列及其趋势图4销售额的预测六、讨论与结论7\n这一份实验报告,主要是学会掌握时间序列预测法、指数平滑法等方法。这一份报告的操作,是三份实验报告里最难完成的一份。我虽然在课上听了老师的讲解,但是还是云里雾里的感觉。后来,自己又拿了书本中的例题,对例题进行一步一步地解剖分析,一点一点地掌握这其中的方法。然后,根据实验报告中的内容,一点一点地斟酌,不断地推敲,才最终掌握了这些方法。这一份的实验内容操作,主要是掌握其中的计算方法,并能够学会对其进行深度地分析。最忌讳地就是不知所云的时候,胡乱地噫定。因为感兴趣,我是对这个实验报告内容进行研究了很久,才得到结果。当然,这报告还要注重美观。其实,系统输出的结果,很多都很粗糙。需要我们对其深度地加工。如果直接利用系统输出的结果,整个报告页面的美观度就会下降很多。但是,稍微对其中的一些细节进行加工后,整体感觉就好很多了。这统计学课程,我是相当感兴趣的。因为之前在学习数学建模的时候,经常需要对数据进行处理。但无奈对excel的强大功能认识不够。我们很多都不得不去学习其他的数学软件的操作。现在,认识到了excel的作用后,以后对数据的处理就方便很多了。7\n实验报告评分表学生姓名念彩娟学号091735013专业年级2009级旅游管理实验项目名称实验三:复合型时间序列分解预测EXCEL处理实验学时4学时评价项目权重评价内容评价结果得分ABCD实验态度20%实验态度端正,遵守实验室守则,严格按照实验要求进行操作。20161412实验过程30%实验项目符合大纲,实验方法科学;步骤操作合理,逻辑条理清晰,符合指导书要求。30242118实验结论与讨论30%实验结论正确,分析、讨论深入。30242118实验报告描述20%语言精炼、流畅、准确、灵活,逻辑性强;结构严谨规范,条理清晰,布局合理,系统严密。20161412总分教师签名7查看更多