计算机算法导引

计算机算法导引

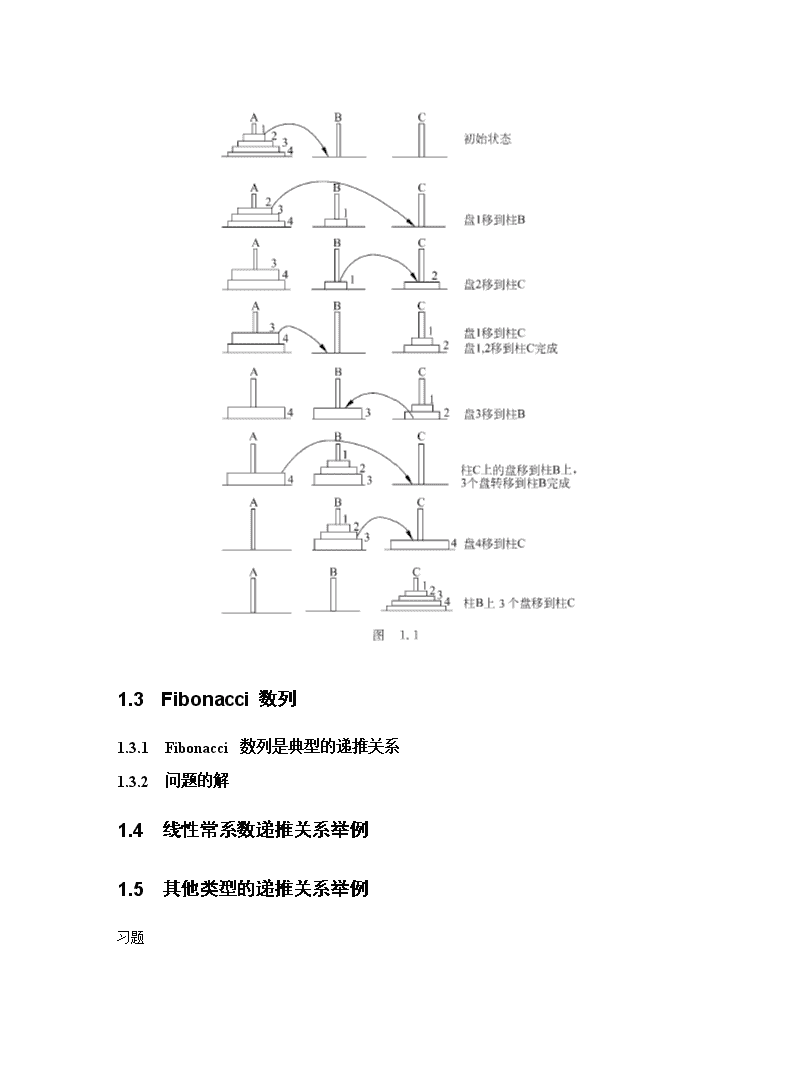
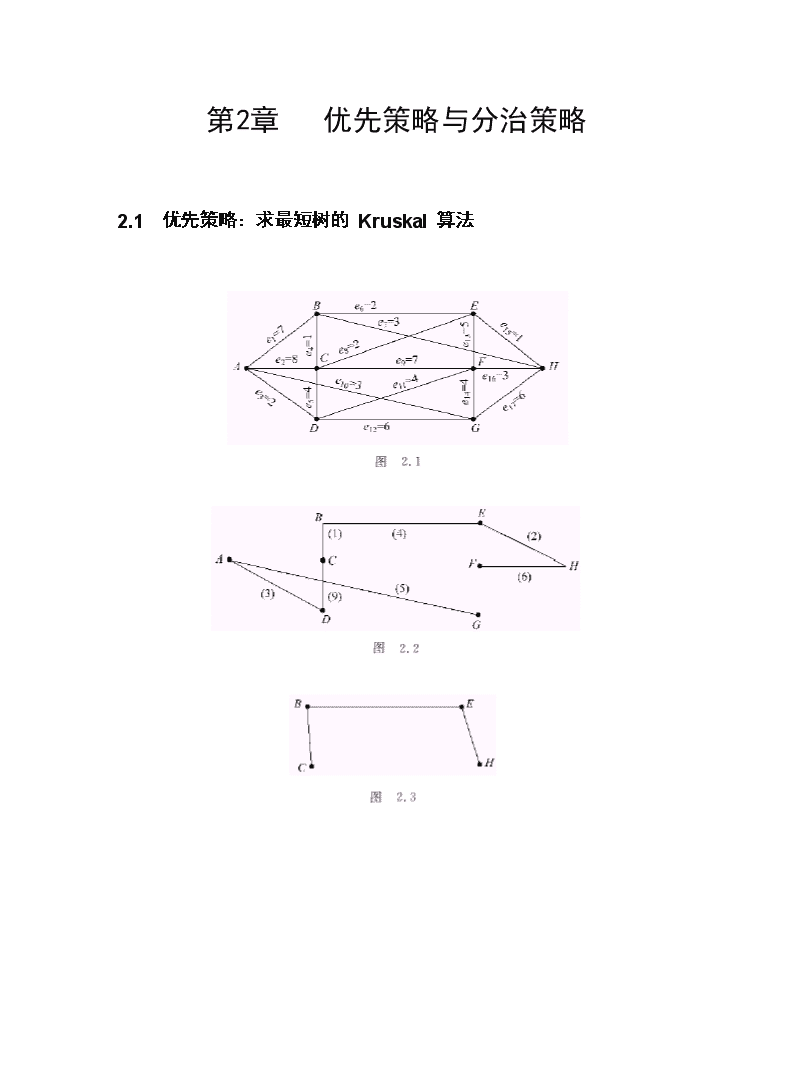
第1部分基本算法第1章数学准备1.1母函数1.2递推关系\n1.3Fibonacci数列1.3.1Fibonacci数列是典型的递推关系1.3.2问题的解1.4线性常系数递推关系举例1.5其他类型的递推关系举例习题\n第2章优先策略与分治策略2.1优先策略：求最短树的Kruskal算法\n2.2求最短树的Prim算法\n2.3求最短路径的Dijkstra算法2.4文件存储问题2.5有期限的任务安排问题2.6数据压缩和Huffman树\n\n\n\n2.7分治策略与二分查找2.8整数乘法2.9矩阵乘积的Strassen算法2.10矩阵乘积的Winograd算法2.11布尔矩阵乘积的分段预处理方法2.12归并排序法\n2.13快速排序法2.14求序列中的第k个元素习题\n第2章动态规划3.1最短路径问题\n3.2最佳原理\n\n3.3流动推销员问题3.3.1算法及例题3.3.2复杂性估计3.4矩阵链乘问题\n3.5最长公共子序列3.6图的任意两点间的最短距离3.7同顺序流水作业的任务安排问题\n3.8可靠性问题3.9最佳二分树3.9.1二分树的一些性质\n3.9.2最佳二分树的构成\n\n习题\n第2章概率算法4.1生日问题4.2概率算法举例\n4.3随机数的产生器4.3.1线性同余式法4.3.2离散对数法4.3.3BBS法4.3.4素数法4.4素数的概率判定算法4.4.1关于素数的若干定理\n4.4.2Fermat数4.4.3MillerRabin的素数概率测试法4.5定理证明的数学准备4.5.1数论的基本知识4.5.2群论的基本知识4.5.3中国剩余定理4.5.4xn≡1modp的解4.6定理A的证明4.7定理B的证明习题\n第2章并行算法5.1并行计算机和并行算法的基本概念\n5.2递推关系的并行计算\n5.3图的并行算法举例\n\n\n5.4矩阵乘积的并行计算\n\n5.5分布计算5.6快速傅里叶变换5.6.1FFT问题的背景5.6.2预备定理5.6.3快速算法\n\n5.6.4傅里叶逆变换5.6.5计算结果的重排\n5.6.6复杂性估计5.7卷积及其应用5.7.1卷积5.7.2多项式的一种快速乘法5.8数论变换5.9排序网络5.9.1引论\n5.9.201原理\n5.9.3Bn型网络\n\n5.9.4Mn归并网络\n5.10Batcher奇偶归并网络\n5.11脉动阵列的并行处理5.11.1矩阵和向量乘法的并行处理\n5.11.2矩阵乘法的并行处理\n5.11.3带状矩阵的并行乘法\n\n习题\n第2章搜索法6.1引论6.2DFS搜索法\n\n6.3无向图的DFS算法\n6.4有向图的DFS算法\n\n6.5互通块问题\n6．6强连通块问题\n6.7BFS算法\n\n6.8拓扑排序6.9minmax搜索法\n6.10流动推销员问题的分支定界法\n图6.256.11同顺序加工任务安排问题\n习题\n第2章数据结构7.1“堆”和“堆集排序法”7.1.1堆\n\n7.1.2堆集排序法\n7.1.3优先级队和二进制堆\n\n\n7.223树\n\n7.3234树\n\n7.4红黑树7.4.1RB树性质7.4.2插入\n\n\n7.4.3删除\n7.5B树7.5.1B树性质7.5.2B树的插入\n\n\n\n7.5.3B树的删除\n7.6关于高度的均衡树7.6.1AVL树——关于高度均衡的二分树\n7.6.2关于高度均衡的二分树的插入和删除\n\n7.7哈希表7.7.1什么是哈希表7.7.2哈希函数的构造方法7.7.3解决冲突的方法\n\n7.7.4哈希算法的分析(线性探测法分析)7.7.5二重哈希法习题\n第2部分若干专题第8章排序算法8.1排序8.2下界估计\n8.3二分插入排序法8.4下溢排序法\n8.5FordJohnson归并插入排序法8.5.1算法的非形式化描述8.5.2一般情形的讨论\n8.5.3算法分析8.6外存排序8.6.1外存归并排序法8.6.2三条带的外存归并排序法\n\n8.6.3阶式归并法\n第9章计算几何及计算数论9.1关于线段问题\n\n9.2凸包问题与Voronoi问题9.2.1凸包问题\n9.2.2Voronoi图9.2.3Voronoi图的构造法\n9.2.4Voronoi图的应用简介9.2.5Voronoi图的拓广\n9.3串匹配9.3.1搜索法9.3.2KMP算法\n9.3.3BM算法9.3.4RK算法9.4数论的算法问题9.4.1求最大公因数9.4.2因数分解之一：Pollardρ法\n9.4.3Dixon随机平方因数分解法9.4.4椭圆曲线因数分解法\n9.5大数模幂运算9.6NmodM9.6.1Barrett归约9.6.2模乘算法9.6.3Montgomery模幂运算9.6.4n是偶数的情况\n第10章线性规划10.1问题的提出\n10.2线性规划的几何意义\n\n10.3单纯形法理论基础\n10.4单纯形法及单纯形表格\n\n10.5改善的单纯形法表格\n10.6对偶原理10.6.1对偶概念10.6.2对偶问题的经济意义10.6.3对偶问题的性质10.6.4对偶定理10.6.5影子价格\n10.7对偶单纯形法\n\n10.8退化情况及其他10.8.1退化情况\n\n10.8.2退化情况的循环不已与Bland法则\n10.9DantzigWolfe分解算法\n10.10整数规划10.10.1问题的提出\n10.10.201规划和DFS搜索法\n\n\n10.10.3分支定界法\n10.11Klee与Minty举例\n\n第3部分复杂性理论与智能型算法第11章算法复杂性理论11.1图灵机\n\n11.2图灵机和算法11.3k条带的图灵机11.4非确定型图灵机11.5停机问题\n\n11.6布尔表达式11.7布尔变量和网络11.8问题的转换\n11.9Cook定理11.10几个NP完备的例子\n\n\n11.11复杂度类11.12近似解法11.12.1任务安排的近似算法\n\n11.12.2装箱问题的近似算法11.12.3流动推销员问题的近似算法\n\n11.12.4顶点覆盖问题的近似算法11.13近代密码学简介11.13.1密码概念11.13.2背包公钥密码11.13.3RSA公钥密码\n第12章智能型算法12.1遗传算法12.2什么是遗传算法12.3TSP问题12.3.1编码12.3.2初始“种群”的生成12.3.3杂交12.3.4变异算术12.3.5模式定理12.4模拟退火算法简介\n\n习题