- 2022-08-30 发布 |
- 37.5 KB |
- 5页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
计算机导论考试
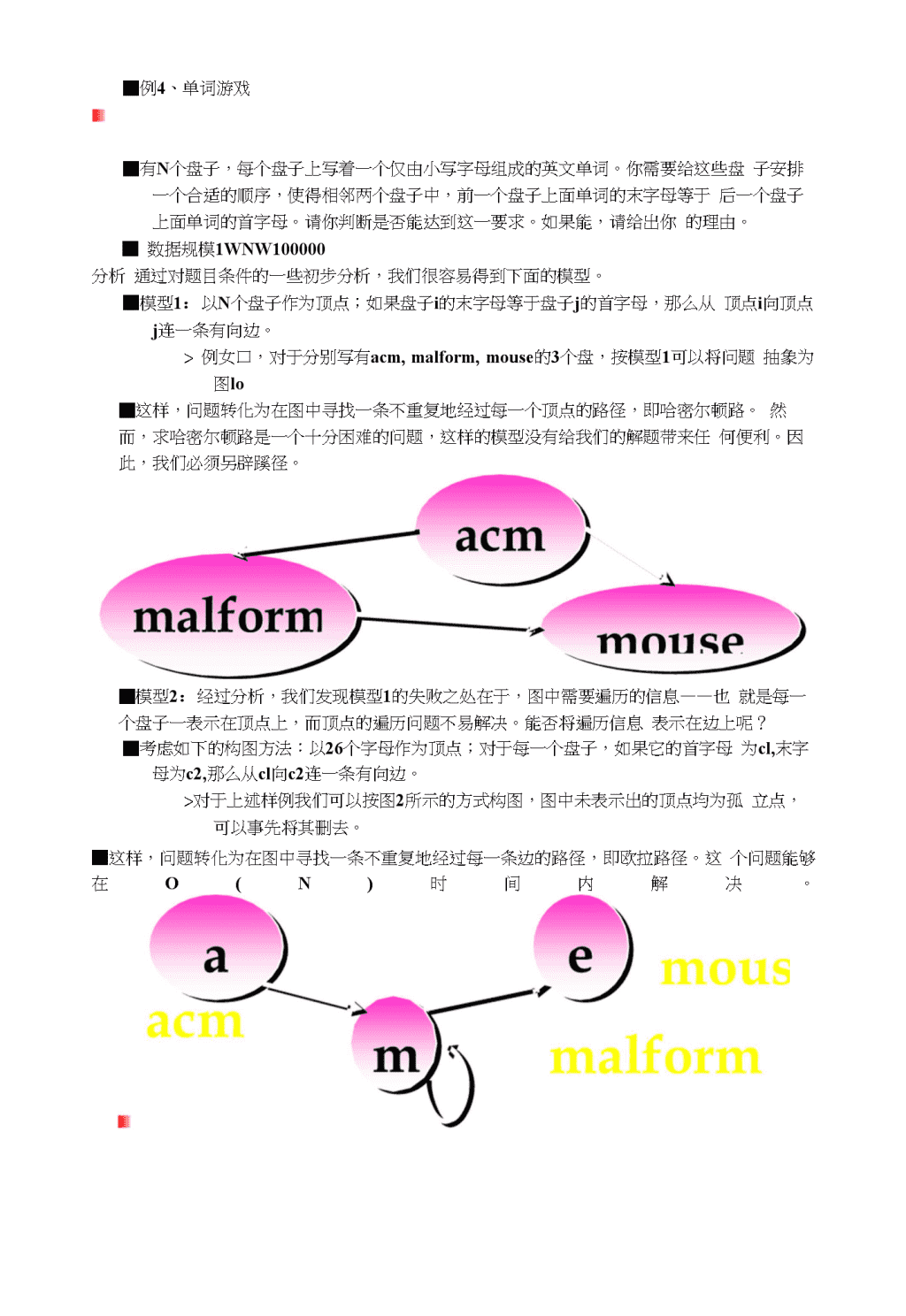
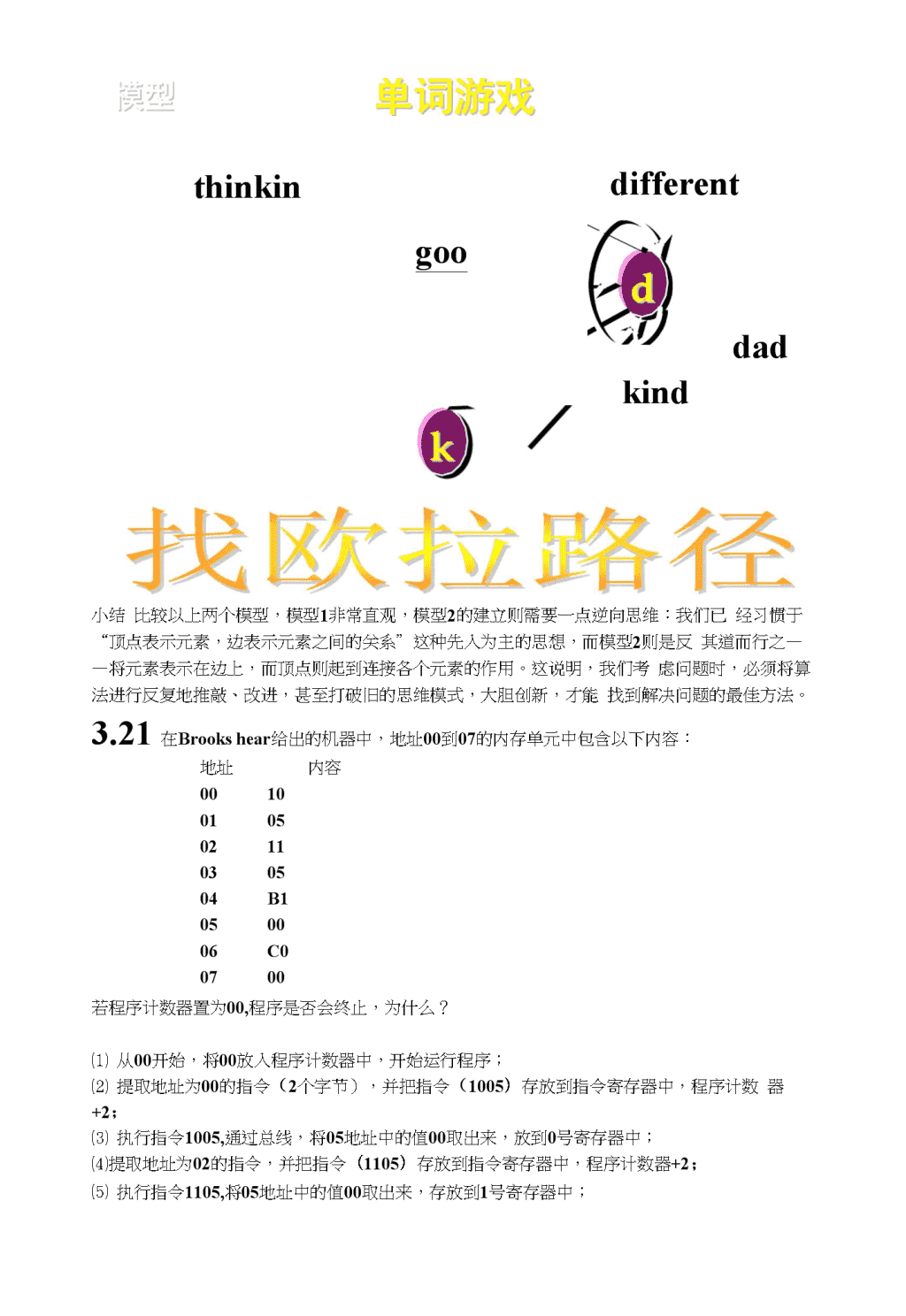
■例4、单词游戏■有N个盘子,每个盘子上写着一个仅由小写字母组成的英文单词。你需要给这些盘子安排一个合适的顺序,使得相邻两个盘子中,前一个盘子上面单词的末字母等于后一个盘子上面单词的首字母。请你判断是否能达到这一要求。如果能,请给出你的理由。■数据规模1WNW100000分析通过对题目条件的一些初步分析,我们很容易得到下面的模型。■模型1:以N个盘子作为顶点;如果盘子i的末字母等于盘子j的首字母,那么从顶点i向顶点j连一条有向边。>例女口,对于分别写有acm,malform,mouse的3个盘,按模型1可以将问题抽象为图lo■这样,问题转化为在图中寻找一条不重复地经过每一个顶点的路径,即哈密尔顿路。然而,求哈密尔顿路是一个十分困难的问题,这样的模型没有给我们的解题带来任何便利。因此,我们必须另辟蹊径。■模型2:经过分析,我们发现模型1的失败之处在于,图中需要遍历的信息——也就是每一个盘子一表示在顶点上,而顶点的遍历问题不易解决。能否将遍历信息表示在边上呢?■考虑如下的构图方法:以26个字母作为顶点;对于每一个盘子,如果它的首字母为cl,末字母为c2,那么从cl向c2连一条有向边。>对于上述样例我们可以按图2所示的方式构图,图中未表示出的顶点均为孤立点,可以事先将其删去。■这样,问题转化为在图中寻找一条不重复地经过每一条边的路径,即欧拉路径。这个问题能够在O(N)时间内解决。\n单词游戏■有6个盘子,每个盘子上分别写着由小写字母组成的英文单词thinking,good,different,dad,dark,kindo试问是否存在一个合适的顺序安排这些盘子,使得相邻两个盘子中,前一个盘子上面单词的末字母等于后一个盘子上面单词的首字母。找哈密顿路\nthinkindifferentgoodadkind小结比较以上两个模型,模型1非常直观,模型2的建立则需要一点逆向思维:我们已经习惯于“顶点表示元素,边表示元素之间的关系”这种先入为主的思想,而模型2则是反其道而行之——将元素表示在边上,而顶点则起到连接各个元素的作用。这说明,我们考虑问题时,必须将算法进行反复地推敲、改进,甚至打破旧的思维模式,大胆创新,才能找到解决问题的最佳方法。3.21在Brookshear给出的机器中,地址00到07的内存单元中包含以下内容:地址内容001001050211030504B1050006C00700若程序计数器置为00,程序是否会终止,为什么?⑴从00开始,将00放入程序计数器中,开始运行程序;⑵提取地址为00的指令(2个字节),并把指令(1005)存放到指令寄存器中,程序计数器+2;⑶执行指令1005,通过总线,将05地址中的值00取出来,放到0号寄存器中;⑷提取地址为02的指令,并把指令(1105)存放到指令寄存器中,程序计数器+2;⑸执行指令1105,将05地址中的值00取出来,存放到1号寄存器中;\n⑹提取地址为04的指令,并把指令(B100)存放到指令寄存器中,程序计数器+2;(7)执行指令B100,因0号寄存器中的数据与1号寄存器中的数据相同,故将数00放到程序计数器中;⑻重复(2)~(7)o由上述分析可见,程序不会终止。即程序不断地从05地址单元中取出数据放到寄存器0和寄存器1中,寄存器0和寄存器1中的数据始终相等,跳转指令总是跳回到程序开始,如此反复,永不终止。4.8就“兔子问题”而言,请问一对兔子14个月内可繁殖成多少对兔子?兔子问题:假设一对刚出生的兔子一个月后就能长大,再过一个月就能生下一对兔子,并且此后每个月都能生一对兔子,且新生的兔子在第二个月后也是每个月生一对兔子。问:在n个月之内可以繁殖成多少对兔子?斐波那契数列:0,1,1,2,3,5,8,13,21,34,・・・规则:F0=0,Fl=l,Fn+2二Fn+l+Fn,月份012345678910111213141兔子01123581321345589144233377一对兔子14个月内可繁殖成377对兔子。补充练习5:辭)用贪婪算法解决背包问题,有3种常用的贪婪准则:准则1:每次都选择价值最大的物品装包。准则2:每次都选择重量最小的物品装包。准则3:每次都选择Vi/Wi值(价值密度)最大的物品装包。设n:物品的个数,Wi:物品i的重量,Vi:物品i的价值,C:背包的重量容量。现在n=3,Wl=70,Vl=60;W2=30,V2=50;W3=40,V3=40;C=110o要求尽可能使装入的物品总价值最大,请写出使用不同准则所选择的物品,并计算其总价值。答:(1)应用准则1,选择物品1和2,总价值为110;(2)应用准则2,选择物品2和3,总价值为90;(3)应用准则3,选择物品2和3,总价值为90;5.27请用伪代码给出求解斐波那契数的递归算法。斐波那契数列:0,1,1,2,3,5,8,13,21,34,...递归基础:F0=0,Fl=l,递归步骤:Fn=Fn-l+Fn-2,n^2unsignedlongF(intn){if(n<0){printf(“参数n应该为非负整数!\n,9);else{if(n<=l)returnn;elsereturnF(n-l)+F(n-2);用递归的方法求非负整数N的阶乘Factor(N)阶乘F(n)=nl的递归定义如下:\n递归基础:F(0)=l;递归步骤:F(/i)=wXF(n-l),unsignedlongFactor(intn){if(n<=l)return1;elsereturnn*Factor(n-l);}}设变量/表示累计乘积结果,变量i表示循环次数。用自然语言对算法描述如下:(1)将1赋给/;(2)将1赋给i;(3)将/Xi赋给/;(4)将i+1赋给i;(5)若上N,转(3)继续;(6)返回/,算法结束。伪代码如下:BEGINIniInfdo{fXinfi+lni}while(i<=N)return(f)ENDC语言程序如下:unsignedlongFactor(intN){intf,i;f=l;for(i=l;i<=N;i++)returnf;查看更多