- 2022-08-29 发布 |
- 37.5 KB |
- 3页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
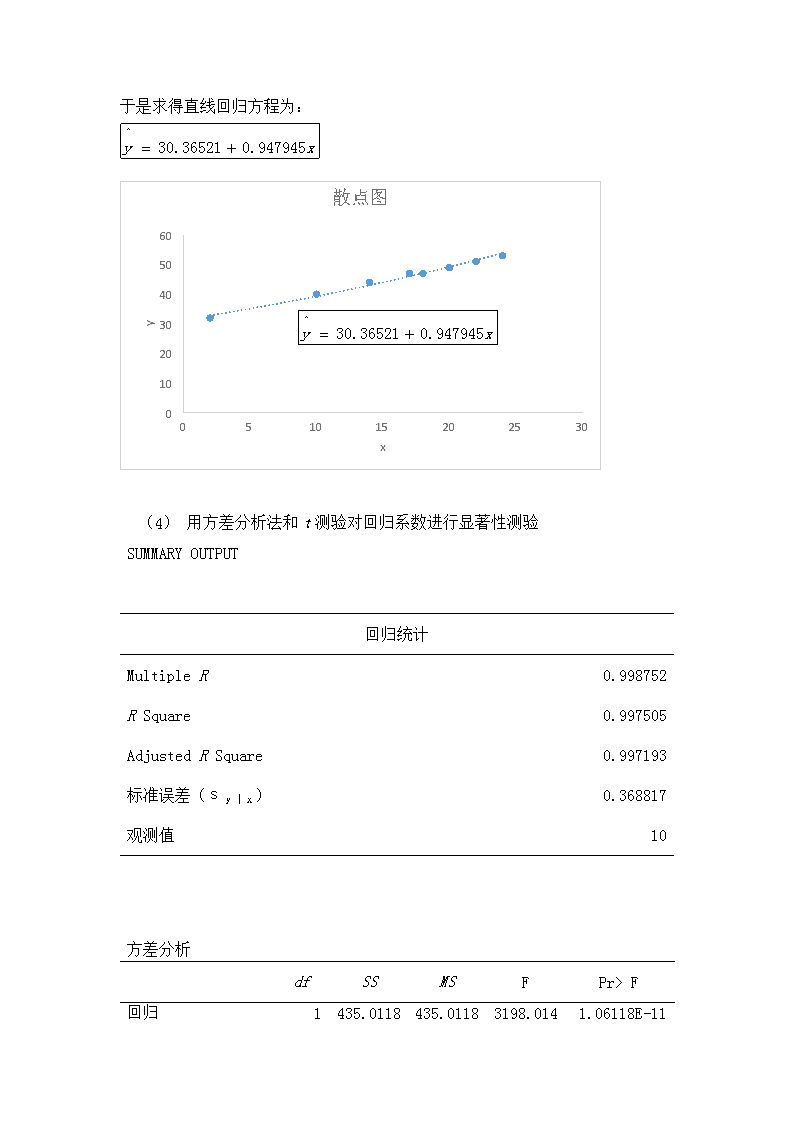
试验统计学实验报告
华南农业大学实验报告某病虫监测站连续10年观察了在秋季第一次平均气温出现低于等于25℃的日期x和同年某种害虫幼虫的暴食期y。变量x和y均以9月1日为1进行统计,数据如下表所示。观察年份1984198519861987198819891990199119921993x202422141821710416y49535144473247403446(1)试求x与y之间的相关系数。xyx1y0.9987515651X与y之间的相关系数是0.998751565。(2)对相关系数进行显著性测验sr=0.017661082|t|=56.55098425>t0.05X与y之间相关显著(3)试求变量y在x上的直线回归方程n=1014714.72645SSx=484.1;44344.320061SSy=436.1;SPxy=458.9于是正规方程为:10a+147b=443147a+2645b=6971可解得:b=0.947945a=30.36521\n于是求得直线回归方程为:(1)用方差分析法和t测验对回归系数进行显著性测验SUMMARYOUTPUT回归统计MultipleR0.998752RSquare0.997505AdjustedRSquare0.997193标准误差(sy|x)0.368817观测值10方差分析 dfSSMSFPr>F回归1435.0118435.01183198.0141.06118E-11\n残差81.0882050.136026总计9436.1 因为p=1.06118E-11<0.05,所以否定原假设,认为Y与X存在显著的线性相关。t测验 Coefficients标准误差tStatP-value下限95.0%上限95.0%Intercept30.36521380.2726187111.383464.71677E-1429.7365530.993874x0.947944640.016762756.5509841.06118E-110.909290.9865994P1=4.72E-14<0.05,否定原假设,a与0有显著差异。P2=1.06E-11,否定原假设,Y与X存在显著的线性关系。(1)如果某一年低于25℃的平均气温出现在9月12日,则有95%把握判断该虫的暴食期出现在什么时期?某一年低于25℃的平均气温出现在9月12日,即x=12。30.36521+0.947945*12=41.74055sy|x=0.3688170.38945741.74055-0.389457=41.3510941.74055+0.389457=42.13001所以有95%的把握说,该虫的暴食期出现在(41.35109,42.13001)之间。查看更多