- 2022-08-29 发布 |
- 37.5 KB |
- 13页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
统计学复习题
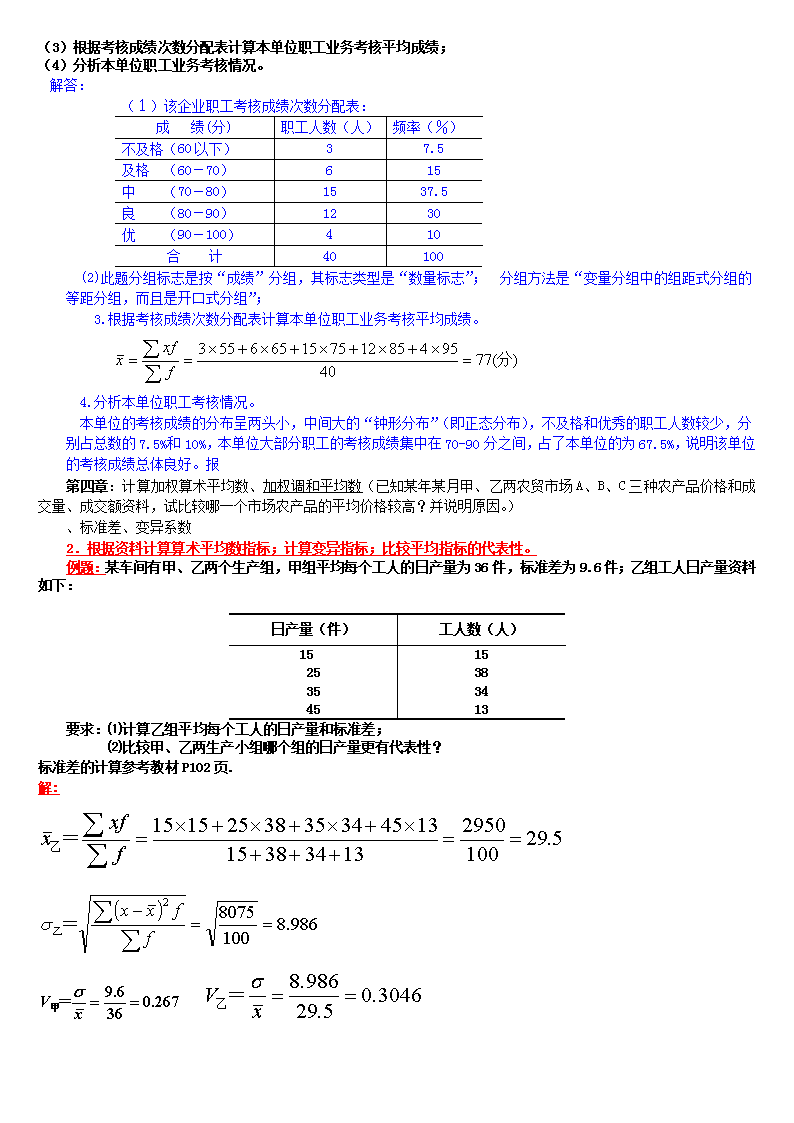
第四部分:简答与计算题复习一、简答题简述品质标志与数量标志的区别并举例说明。P复习指导42+教材13答:统计标志通常分为品质标志和数量标志两种。品质标志表明总体单位属性方面的特征,无法量化,其标志表现只能用文字来表示;如职工的性别、文化程度,企业的经济成份,产品品牌等。品质标志本身不能直接汇总为统计指标,只有对其标志表现所对应的单位进行汇总综合才能形成统计指标即总体单位总量。数量标志表明总体单体数量的特征,其标志表现可以用数值来表示,即标志值.如职工的年龄,工资,身高。数量标志可以直接汇总为统计指标。举例说明如何理解调查单位与填报单位的关系答:调查单位是调查资料的直接承担者,报告单位是调查资料的提交者,二者有时一致,有时不一致。如,对某市工业企业生产经营情况调查,该市所有的工业企业是调查对象,而每一工业企业是调查单位,同时又是报告单位;又如对某市工业企业职工收入状况调查,该市所有工业企业的全体职工是调查对象,每一职工是调查单位,而每一工业企业是报告单位。p学习指导63&P书33简述变量分组的种类及应用条件。P学习指导68答:按数量标志分组的目的并不是单纯确定各组在数量上的差别,而是要通过数量上的变化来区分各组的不同类型和性质。数量标志的分组的种类及应用条件从以下几个方面来说明:一是单项式分组和组距式分组。对离散变量根据情况既可用单项式分组,也可用组距式分组。1.离散变量如果变量值的变动幅度小,就可以一个变量值对应一组,称单项式分组。如,居民家庭按儿童数或人口数分组,均可采用单项式分组。2.离散变量如果变量值的变动幅度很大,变量值的个数很多,则把整个变量值依次划分为几个区间,各个变量值则按其大小确定所归并的区间,区间的距离称为组距,这样的分组称为组距式分组。二是等距分组和不等距分组。对连续变量由于不能列举其变量值,只能采用组距式的分组方式,且相邻的组限必须重叠。(如以总产值、商品销售额、劳动生产率、工资等为标志进行分组,就只能是相邻组限重叠的组距式分组。)分组时采用等距分组还是不等距分组,取决于研究对象的性质特点。在连续变量标志值变动比较均匀的情况下宜采用等距分组。等距分组便于各组单位数和标志值直接比较,也便于计算各项综合指标。在连续变量标志值变动很不均匀的情况下宜采用不等距分组。不等距分组有时更能说明现象的本质特征。简述结构相对指标和比例相对指标有什么不同并举例说明P复习指导45答:结构相对指标是以总体总量为比较标准,计算各组总量占总体总量的比重,来反映总体内部组成情况的综合指标。如:各工种的工人占全部工人的比重、升学率、合格率等。比例相对指标是总体不同部分数量对比的相对数,用以分析总体范围内各个局部之间比例关系和协调平衡状况。如:轻重工业比例、男女比等。二、计算分析题(要求写出公式和计算过程,结果保留两位小数。本题共50分)(计算参考作业及期末复习指导。)第三章:编制次数分配数列1.根据所给资料分组并计算出各组的频数和频率,编制次数分布表;根据整理表计算算术平均数.例题:某单位40名职工业务考核成绩分别为:68898884868775737268758297588154797695767160906576727685899264578381787772617081单位规定:60分以下为不及格,60─70分为及格,70─80分为中,80─90分为良,90─100分为优。要求:(1)将参加考试的职工按考核成绩分为不及格、及格、中、良、优五组并编制一张考核成绩次数分配表;(2)指出分组标志及类型及采用的分组方法;\n(3)根据考核成绩次数分配表计算本单位职工业务考核平均成绩;(4)分析本单位职工业务考核情况。解答:(1)该企业职工考核成绩次数分配表:成绩(分)职工人数(人)频率(%)不及格(60以下)37.5及格(60-70)615中(70-80)1537.5良(80-90)1230优(90-100)410合计40100(2)此题分组标志是按“成绩”分组,其标志类型是“数量标志”; 分组方法是“变量分组中的组距式分组的等距分组,而且是开口式分组”; 3.根据考核成绩次数分配表计算本单位职工业务考核平均成绩。4.分析本单位职工考核情况。本单位的考核成绩的分布呈两头小,中间大的“钟形分布”(即正态分布),不及格和优秀的职工人数较少,分别占总数的7.5%和10%,本单位大部分职工的考核成绩集中在70-90分之间,占了本单位的为67.5%,说明该单位的考核成绩总体良好。报第四章:计算加权算术平均数、加权调和平均数(已知某年某月甲、乙两农贸市场A、B、C三种农产品价格和成交量、成交额资料,试比较哪一个市场农产品的平均价格较高?并说明原因。)、标准差、变异系数2.根据资料计算算术平均数指标;计算变异指标;比较平均指标的代表性。例题:某车间有甲、乙两个生产组,甲组平均每个工人的日产量为36件,标准差为9.6件;乙组工人日产量资料如下: 日产量(件)工人数(人)1525354515383413要求:⑴计算乙组平均每个工人的日产量和标准差;⑵比较甲、乙两生产小组哪个组的日产量更有代表性?标准差的计算参考教材P102页.解:\n类似例题讲解:甲、乙两个生产小组,甲组平均每个工人的日产量为36件,标准差为9.6件;乙组工人日产量资料如下:日产量(件)工人数(人)10-2020-3030-4040-5018393112计算乙组平均每个工人的日产量,并比较甲、乙两生产小组哪个组的日产量更有代表性?解答:第五章:计算抽样平均误差、简单随机抽样条件下估计总体平均数和总体成数的区间范围和总量指标的区间范围。3.采用简单重复抽样的方法计算成数(平均数)的抽样平均误差;根据要求进行成数(平均数)的区间估计及总数的区间估计。例题1:某工厂有1500个工人,用简单随机重复抽样的方法抽出50个工人作为样本,调查其月平均产量水平,资料如下:日产量(件)524534540550560580600660工人数(0人)469108643要求:(1)计算样本平均数和抽样平均误差。(2)以95.45%(t=2)的可靠性,估计该厂工人的月平均产量和总产量的区间。解答: n=50,N=1500,t=2(1)计算样本平均数和抽样平均误差\n=560(件)s(标准差ss=(件)计算重复抽样的抽样平均误差:(2)以95.45%的可靠性估计该厂工人的月平均产量和总产量的区间。计算重复抽样的抽样极限误差:该厂工人的月平均产量重复抽样的区间范围是:则,该厂工人的月平均产量区间范围是在550.82件至569.18件之间。总产量为:550.82*1500=826230件 569.18*1500=853770件该厂工人的总产量的区间范围是在826230件至853770件之间。例题2:采用简单随机重复抽样的方法,在2000件产品中抽查200件,其中合格品190件.要求:(1)计算合格品率及其抽样平均误差(2)以95.45%的概率保证程度(t=2)对合格品率和合格品数量进行区间估计。解答:①已知:n=200 N=2000 F(t)=95.45% t=2合格品率:p==95%合格品率的抽样平均误差:合格品率的区间范围:下限=\n上限=即合格品率的区间范围为:91.92%--98.08%合格品数量的区间范围为:91.92%*2000----98.08%*20001838.4件~1961.6件之间.第七章:计算相关系数、建立回归方程并解释回归系数的含义、预测因变量的估计值。4.计算相关系数;建立直线回归方程并指出回归系数的含义;利用建立的方程预测因变量的估计值。例题:某企业上半年产品产量与单位成本资料如下:月 份产量(千件)单位成本(元)123456234345737271736968要求:(1)计算相关系数,说明两个变量相关的密切程度。(2)配合回归方程,指出产量每增加1000件时,单位成本平均变动多少? (3)假定产量为6000件时,单位成本为多少元?解答:回归方程计算表:月份产量x单位成本yx2y2xy123456234345737271736968491691625532951845041532947614624146216284219276340合计2142679302681481n=6=21=4262=792=30268=1481(1)相关系数:=-0.9090说明产量x和单位成本y之间存在着高度负相关关系。见教材183(2)设直线回归方程为yc=a+bxn=6=21=4262=792=30268=1481=(1481-1/6*21*426)/(79-1/6*21*21)=-1.82\n=426/6-(-1.82)*21/6=77.37则yc=77.37-1.82x在这里说明回归系数b的含义,即产量每增加1000件时,单位成本平均降低1.82元.(3)假定产量为6000件,即x=6时,单位成本为:则yc=77.37-1.82x=77.37-1.82*6=66.45(元).即单位成本为:66.45元.世面2.根据企业产品销售额(万元)和销售利润率(%)资料计算出如下数据:n=7=1890=31.12=5355002=174.15=9318要求:(1)确定以利润率为因变量的直线回归方程.(2)解释式中回归系数的经济含义.(3)当销售额为500万元时,利润率为多少?参考答案:(1)确定以利润率为因变量的直线回归方程:Y=-5.5+0.037x(2)解释式中回归系数的经济含义:产品销售额每增加1万元,销售利润率平均增加0.037%.(3)当销售额为500万元时,利润率为:Y=12.95%第八章:数量指标综合指数、质量指标综合指数的计算;加权算术平均数指数和加权调和平均数指数的计算;从相对数和绝对数角度对总量指标的变动进行因素分析。5.计算综合指数及平均指数(加权、调和)并同时指出变动绝对值、计算平均数指数。此类计算的知识背景:综合指数的计算与分析(1)数量指标指数 此公式的计算结果说明复杂现象总体数量指标综合变动的方向和程度。 (-)此差额说明由于数量指标的变动对价值量指标影响的绝对额。(2)质量指标指数 此公式的计算结果说明复杂现象总体质量指标综合变动的方向和程度。 (-)此差额说明由于质量指标的变动对价值量指标影响的绝对额。平均指数计算是综合指数的变形,也可以是独立意义的平均指标指数。在得不到全面资料的情况下必须运用平均指数。平均指数是从个体指数出发来编制总指数的,计算形式为算术平均数指数和调和平均数指数。\n(1)加权算术平均指数的编制,是以基期总量为权数对个体数量指标指数进行加权算术平均,以此计算的加权平均数指数等于数量指标综合指数。加权算术平均数指数=k=q1/q0式中,K表示数量指标的个体指数,表示基期的某个总量指标。也就是说,要编制加权算术平均数指数,一要掌握数量指标个体指数,二要掌握基期总量。(2)加权调和平均数指数的编制,是以报告期总量为权数对个体质量指标指数进行加权调和平均,据此计算的加权调和平均数指数等于质量指标综合指数。加权调和平均数指数=k=p1/p0式中,K表示质量指标个体指数,表示报告期的某个总量指标。也就是说,要编制加权调和平均数指数,一要掌握质量指标个体指数,二要掌握报告期总量。综合指数主要适用于全面资料编制,而平均指数既可以依据全面资料编制,也可以依据非全面资料编制;综合指数一般采用实际资料做权数编制,平均指数在编制时,除了用实际资料做权数外,也可以用估算的资料做权数。相对数变动分析:= × 绝对额变动分析:-=(-)+(-)例题1:某企业生产两种产品的资料如下:产品单位产量q单位成本p(元)基期计算期基期计算期甲乙件公斤50150601608121014要求:(1)计算两种产品总成本指数及总成本变动的绝对额;(2)计算两种产品产量总指数及由于产量变动影响总成本的绝对额;(3)计算两种产品单位成本总指数及由于单位成本影响总成本的绝对额。解答:(1)计算两种产品总成本指数及总成本变动的绝对额;单位产量q单位成本p(元)基期q0计算期q1基期p0计算期p1甲乙件公斤50150601608121014总成本变动绝对额:\n(元)(2)计算两种产品产量总指数及由于产量变动影响总成本的绝对额;产量总指数:由于产量变动而增加的总成本:(3)计算两种产品单位成本总指数及由于单位成本影响总成本的绝对额。单位成本总指数:由于单位成本而增加的总成本:总结:以上计算可见:通过指数体系分析如下:总成本指数=产量总指数*单位成本总指数129.09%=109.09%*118.33% 总成本变动绝对额=产量变动绝对额+单位成本变动绝对额640=200+440可见,两种产品的总成本增加了29.09%,增加了640元;其中由于产量增加了9.09%,而使总成本增加了200元,由于单位成本增加了18.33%,而使总成本增加了440元。类似例题讲解:某企业生产三种产品的资料如下:产品单位产量单位成本(元)基期计算期基期计算期\n甲乙丙件公斤台1005001501205002001545910557要求:(1)计算三种产品单位成本总指数及由于单位成本影响总成本的绝对额。(2)计算三种产品产量总指数及由于产量变动影响总成本的绝对额;(3)计算三种产品总成本指数及总成本变动的绝对额;解答:(1)三种产品的单位成本总指数:由于单位成本而增加的总成本:(2)三种产品的产量总指数:由于产量变动而增加的总成本:(3)指数体系分析如下: 总成本指数=产量总指数*单位成本总指数总成本变动绝对额=产量变动绝对额+单位成本变动绝对额可见,三种产品的总成本增加了18.7%,增加了4750元;其中由于产量增加了2.96%,而使总成本增加了750元,由于单位成本增加了15.33%,而使总成本增加了4000元。例题2.某商店两种商品的销售额和销售价格的变化情况如下:商品单位销售额pq(万元)1996年比1995年销售价格提高(%)p1/po1995年p0q01996年p1q1甲乙米件12040130361012要求:(1)计算两种商品销售价格总指数和由于价格变动对销售额的影响绝对额。\n(2)计算销售量总指数,计算由于销售量变动,消费者增加(减少)的支出金额。解答:销售价格总指数=由于价格上升支出的货币金额多:==166-142.32=23.68(万元)(2)销售量总指数=销售额指数÷销售价格指数由于销售量减少,消费者减少的支出金额:销售量变动绝对额=销售额总变动额-销售价格绝对额=(166-160)-(166-142.32)=-17.68(万元)类似例题讲解如下: 某商店商品销售资料如下:商品类别销售额(万元)2003年比2002年价格升降(%)p1/p02002年2003年百货食品50287534-25(1)试计算零售商品销售价格指数和销售量指数;(2)由于价格降低消费者少支出的货币金额。解答:(1)销售价格指数==99.53%销售量指数=销售额指数÷销售价格指数=140.40%(2)由于价格降低少支出的货币金额==109-109.51=-0.51(万元)例题3:某商店三种商品的销售资料如下:商品名称销售额pq(万元)今年销售量\n比去年增长%k=q1/q0基期p0q0报告期p1q1甲1504808乙2002405丙40045015试计算:⑴销售额指数及销售额增加绝对值。⑵销售量指数及由销售量变动而增加的销售额。(3)计算商品销售价格总指数和由于价格变动对销售额的影响绝对额。商品销售价格指数.解答:(1)销售额指数=(万元)(2)销售量总指数=由于销售量增长10.93%,使销售额增加:(万元)第九章:计算各期环比、定基发展速度、增长速度、年平均增长量、平均发展速度、平均增长速度;求解an;时期数列和间断时点数列序时平均数的计算。6.根据资料计算序时平均数(总量指标及相对、平均指标动态数列);根据资料利用平均发展速度指标公式计算期末水平。计算序时平均数的知识背景(两种情况)①由时期数列计算 ②由时点数列计算 时点数列有连续时点数列和间断时点数列之分,其计算方法也不相同。在间断时点数列的条件下计算又有两种情况:若间断的间隔相等,则采用“首末折半法”计算。公式为: 若间断的间隔不等,则应以间隔数为权数进行加权平均计算。公式为:(3)相对指标动态数列:例题1:某商店2007年商品库存资料如下:(单位:万元)\n1月1日:5.2;7月3l日:3.6;1月31日:4.8;8月3l日:3.4;2月28日:4.4;9月30日:4.2;3月31日:3.6;10月31日:4.6;4月30日:3.2;11月30日:5.0;5月31日:3.0;l2月31日:5.6。6月30日:4.0;根据上述资料,计算各季度平均库存额和全年平均库存额。解:根据得:第一季度平均库存额==4.5万元第二季度平均库存额=3.3万元第三季度平均库存额=3.7万元第四季度平均库存额=4.8万元全年平均库存额==4.41万元。例题2:某企业总产值和职工人数的资料如下:月份3456月总产值(万元)月末职工人数(千人)11506.511706.712006.913707.1试计算该企业第二季度平均每月全员劳动生产率(元/人)解:根据公式 (万元)(千人)第二季度月平均全员劳动生产率为(万元/千人)=1833.33(元/人)\n例题3:某地区历年粮食产量资料如下:年份19951996199719981999粮食产量(万斤)300472560450700要求:(1)计算各年的逐期增长量、累积增长量、环比发展速度、定基发展速度;(2)计算1995年-1999年该地区粮食产量的年平均增长量和粮食产量的年平均发展速度;(3)如果从1999年以后该地区的粮食产量按8%的增长速度发展,2005年该地区的粮食产量将达到什么水平?解答:(1)计算各年的逐期增长量、累积增长量、环比发展速度、定基发展速度;计算结果如下表:时间19951996199719981999粮食产量(万斤)逐期增长量(万斤)累计增长量(万斤)环比发展速度(%)定基发展速度(%) 300--472172172157.3157.356088260118.6186.7450-11015080.4150700250400155.6233.3(2)计算1995年-1999年该地区粮食产量的年平均增长量和粮食产量的年平均发展速度;粮食产量的年平均增长量=( 700-300)÷4=100(万斤)粮食产量的年平均增长速度==24%(3)如果从1999年以后该地区的粮食产量按8%的增长速度发展,2005年该地区的粮食产量将达到什么水平?2005年该地区的粮食产量:1586.87(万斤)查看更多