- 2022-08-29 发布 |
- 37.5 KB |
- 15页

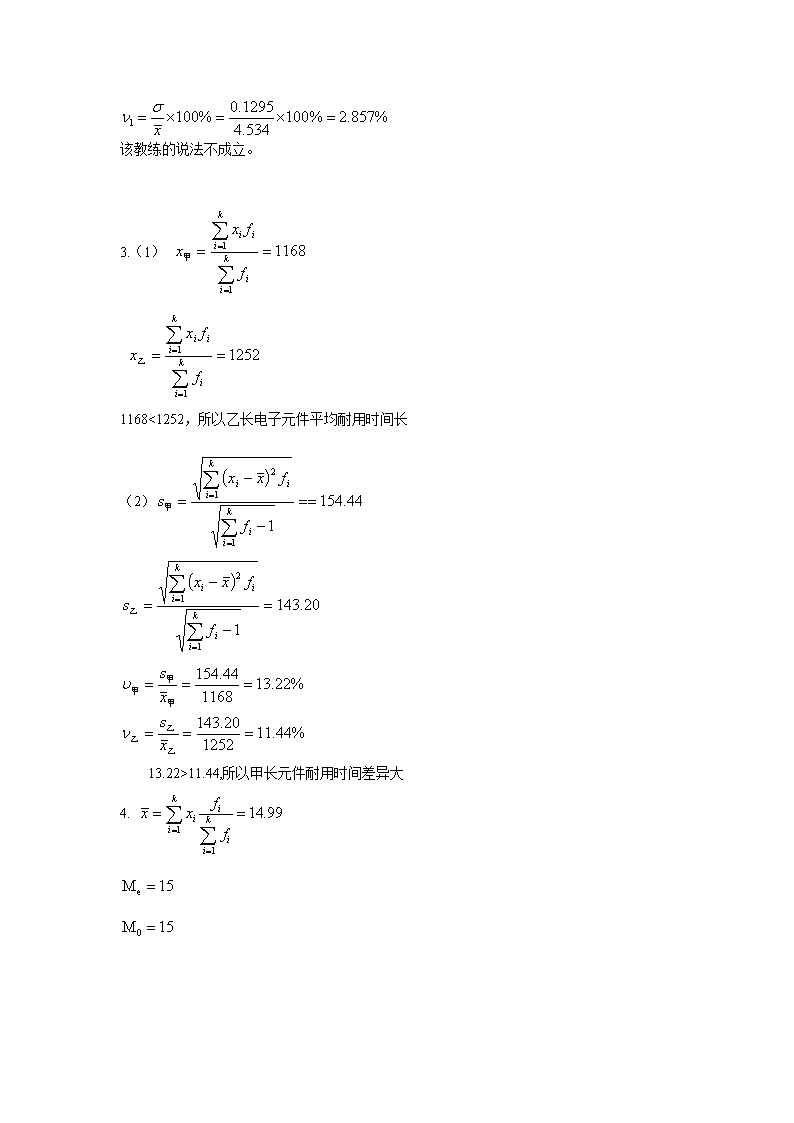

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
统计学课后题答案
《统计学》各章参考答案四、计算题1.乙的代表性强2.\n该教练的说法不成立。3.(1)1168<1252,所以乙长电子元件平均耐用时间长(2)13.22>11.44,所以甲长元件耐用时间差异大4.\n5.6.(1)(2)将所以数据由高到低排序(3)7.\n9.乙班的考核结果明显好于甲班。从离散系数看,乙班为4.04%,甲班为12.85%;从极差来看,乙班为11,甲班为36;从分布来看,乙班基本为正态或钟型分布,甲班明显为左偏分布。10.(1)计算均值和标准差系数来评价优劣(2)所以选择A第五章抽样分布与参数估计四、计算题2.(1)(2)3.n=80>30,大样本,因此用正态分布来估计置信区间(69.29,70.11)4.p=240/400=0.6,np=240>5,n(1-p)=160>5,大样本,因此用正态分布来估计置信区间(55.2%,64.8%)5.p=20/1000=0.02,大样本,因此用正态分布来估计置信区间((0.86%,3.14%))6.首先计算平均每户居民的需求量大样本,因此用正态分布来估计置信区间\n(9.412,10.588)供应1000户,所以最少应准备10.588万kg7.已知N,可以用两种方法放回抽样代入数据n=661代入数据n=7078.其中代入数据n=3859.代入数据得置信区间(0.02,3.98)kg10.代入数据得置信区间为(-0.05%,10.05%)11.代入数据得置信区间为(0.0147,0.0324)第六章假设检验四、计算题1.小样本,方差已知,双侧检验。。。,(P值=0.067),不拒绝原假设,可以认为现在生产的铁水平均含碳量为4.55.2.大样本,方差未知,右侧检验。。。,(P值=0.006),拒绝原假设,厂家声明不可信。3.小样本,方差未知,右侧检验。。由样本数据得到,\n,,,(P值=0.002),拒绝原假设,可以说平均每个调查员每周完成的调查次数大于53次。4.。P=35/60=58.33%,,,(P值=0.099),不拒绝原假设,没有充分证据拒绝银行的声称。5.一个总体方差检验,右侧。。。,不拒绝原假设,即可以认为该线路的运行时间稳定性达到了公司的要求。6.独立样本的均值之差检验,双侧,大样本,方差未知。,,(P值=0.008),拒绝原假设,存在显著差异。7.两总体均值之差检验,匹配小样本。,经计算,,。,(P值=0.002),拒绝原假设,健身课程有效。8.换题9.两总体方差比检验,双侧。。,1.939,拒绝原假设,两个总体方差不相等。第七章方差分析三、计算题1、解::四个行业之间的服务质量相同;\n:四个行业之间的服务质量不完全相同。则由Excel表得:方差分析差异源SSdfMSFP-valueFcrit组间1456.6093485.53623.0.3.12735组内270819142.5263总计4164.60922 因此F=3.41,由于3.13<3.41=F,所以拒绝原假设,即可以认为四个行业之间的服务质量有显著差异。2、解::三个企业生产的电池的平均寿命相同;:三个企业生产的电池的平均寿命不完全相同。则由Excel表得:差异源SSdfMSFP-valueFcrit组间615.62307.817.068390.000313.组内216.41218.03333总计83214 因此F=17.07,3.89<17.07=F,所以拒绝原假设,即可以认为三个企业生产的电池的平均寿命有显著差异。3、解:(1)已知n=30,k=3,MSA=210,SSE=3836因此SSA=(k—1)MSA=420,MSE=SSE/(n—k)=142.074F=MSA/MSE=1.478SST=SSA+SSE=4256,因此方差分析表为差异源SSdfMSFP-valueFcrit组间42022101.4780.3.组内383627142.074———总计425629————(2):三种方法组装的产品数量相同;:三种方法组装的产品数量不完全相同。因为3.35>1.478=F,因此不能推翻原假设,即不能认为三种方法组装的产品数量有显著差异。4、解:行因素(品种)::种子的品种对收获量没有显著影响;\n:种子的品种对收获量有显著影响。列因素(施肥方案)::施肥方案对收获量没有显著影响;:施肥方案对收获量有显著影响。则由Excel表得:差异源SSdfMSFP-valueFcrit行19.06744.766757.0.3.列18.181536.06059.0.3.误差7.901120.总计45.149519 由于,所以拒绝原假设,即种子的品种对收获量有显著影响。由于,所以拒绝原假设,即施肥方案对收获量有显著影响。5、解:行因素(品种)::地区对食品的销售量没有显著影响;:地区对食品的销售量有显著影响。列因素(施肥方案)::包装方法对食品的销售量没有显著影响;:包装方法对食品的销售量有显著影响。则由Excel表得:差异源SSdfMSFP-valueFcrit行22.22222211.111110.0.6.列955.55562477.77783.0.6.误差611.11114152.7778总计1588.8898 由于,所以不能拒绝原假设,即不能认为地区对食品的销售量有显著影响。由于,所以不能拒绝原假设,即不能认为包装方法对食品的销售量有显著影响。\n第八章相关与回归分析三.计算题1.(1),两个变量有较强的负相关关系。 (2)产量每增加1000件时,单位成本平均变动-1.818元。(3)假定产量为6000件时,单位成本为66.44元。2.(1)(2)(3)3.(1)方差分析表 dfSSMSFSignificanceF回归分析1.6.6399.2.17E-09残差1040158.074015.807总计11.67 (2)=0.97由广告费用引起的销售额的变差变动的比例是97%(3),回归系数的含义是广告费用增加(减少)一个单位,销售额平均增加(减少)1.42\n第九章时间序列分析与预测四.计算题:1..2.周1234567数值8131517169-三期移动平均---12151614误差---51-7-误差平方---25149-由上表可知,第七周的预测值=14;均方误差=(25+1+49)/3=26.33.3.周1234567数值8131517169-指数平滑预测-8.009.0010.2011.5612.4511.76误差-5.006.006.804.44-3.45-误差平方-25.0036.0046.2419.7111.89-由上表可知,第七周的预测值=11.76,均方误差=(25+36+46.24+19.71+11.89)/5=27.77,与上题比较均方误差可知,三期移动平均比α=0.2的指数平滑更适合预测.计算可得,α=0.4的指数平滑预测的均方误差=22.53,所以比α=0.2的指数平滑更适合预测.4.期12345678910111213数值909294939394959492939493-三期移动平均预测---92.0093.0093.3393.3394.0094.3393.6793.0093.0093.33误差---1.000.000.671.670.00-2.33-0.671.000.00-误差平方---1.000.000.442.780.005.440.441.000.00-期12345678910111213数值909294939394959492939493-\n指数平滑预测-90.0090.4091.1291.5091.8092.2492.7993.0392.8392.8693.0993.07误差-2.003.601.881.502.202.761.21-1.030.171.14-0.09-误差平方-4.0012.963.532.264.857.631.461.060.031.300.01-三期移动平均预测的均方误差=1.23,α=0.2的指数平滑预测的均方误差=3.56,所以三期移动平均更适合预测,预测值为93.33%.5.市场价格99.599.399.499.699.899.799.8100.599.999.799.699.6-三期移动平均预测---99.4099.4399.6099.7099.77100.00100.07100.0399.7399.63四期移动平均预测----99.4599.5399.6399.7399.9599.9899.9899.9399.70三期移动平均预测的均方误差=0.12,四期移动平均预测的均方误差=0.14,所以三期移动平均预测更适合预测,下一月预测值=99.63(元).6.签约数243523262832223124312423-移动平均预测---27.328.025.728.727.328.325.728.726.326.0指数平滑预测-24.026.225.625.626.127.326.227.226.627.426.826.0三期移动平均预测的均方误差=20.0,α=0.2的指数平滑预测的均方误差=27.8,所以三期移动平均更适合预测.下一月的签约数预测值=26(套).7.股票价格7.357.47.557.567.67.527.527.77.627.55-α=0.2平滑预测-7.3507.3607.3987.4307.4647.4757.4847.5277.5467.547α=0.3平滑预测-7.3507.3657.4217.4627.5047.5097.5127.5687.5847.574α=0.2的指数平滑预测的均方误差=0.017,α=0.3的指数平滑预测的均方误差=0.013,所以α=0.3的指数平滑更适合预测,第十一周的预测值=7.574.8.从图中看出,该地区空调销售量时间序列呈现线性增长趋势,设线性趋势方程为:式中为时间变量,代表2001年,代表2000年,依次类推。根据最小二乘法,\n即趋势方程为:。将代入上式得.即,2007年的销售额预测值是79.84万元.b=0.69,表示销售额平均每年增长0.69万元.9.销售额序列呈现出指数增长趋势.将原销售额序列取自然对数得到对数销售额序列.从右上图可以看出,对数保有量已经表现出线性增长趋势,因此,可以对对数保有量序列建立线性趋势模型。根据最小二乘法可以得到趋势方程:将代入上述方程得2006年对数销售额的预测值:将其转换为保有量的预测值为:(万辆)10.第8题趋势方程:,其中,第9题对数趋势方程:,其中,11.四个季度指数分别为:0.76691.15331.21790.8619剔除季节变动后的序列为:36.5174.5777.1871.9362.5991.9193.6095.13106.93121.39126.45139.22130.40140.46142.87150.82166.92163.01162.58183.31200.82180.35180.64199.55234.73208.09213.48269.16对上述序列利用最小二乘法建立趋势方程:,其中,\n将代入上述趋势方程得2007年各季的趋势预测值,241.51,248.25,255.00,261.74将上述预测值分别乘以四个季度指数0.7669,1.1533,1.2179,0.8619得最终的预测值,185.20,286.32,310.56,225.60第十章指数三、计算题1.(1)(2)2.(1)(2)(3)3.(1)(2)或4.\n从绝对数来看报告期销售额比基期销售额增加了元,是由于价格的提高使销售额增加了元和销售量的提高使销售额增加了元共同作用的结果。从相对数来看报告期的销售额比基期上升了107.43%时由于价格的上升使销售额上升了20%和销售量的增加使销售额上升了72.86%共同作用的结果。5.(1)(2)(3)=第十一章统计综合评价一、选择题1.B2.A3.D4.A5.C6.A二、思考题(略)三、计算题1.计算结果见表,分析略。\n指标标准值权数报告期基期增减(1)(2)(3)(4)=(3)/(1)*(2)(5)(6)=(5)/(1)*(2)(7)=(4)-(6)综合指数%———93.93—96.31-2.38总资产贡献率%10.7209.818.3210.9920.56-2.24资产保值增值率%12016126.9416.93121.2316.160.77资产负债率%601265.1610.4565.1910.470.02流动资金周转率%1.52151.52151.5715.49–0.49成本费用利润率%3.71142.7310.32.9811.25–0.95全员劳动生产率1650010164149095157519.550.4产品销售率%961395.8612.9883830.152.计算结果见表,分析略。甲806897.3379.3173.337662.677063.6468.3365.7161.11乙9096102.6799.1086.679697.339690.9193.3394.2998.89合计甲商店综合得分:73.94乙商店综合得分:94.81查看更多