- 2022-08-29 发布 |
- 37.5 KB |
- 47页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
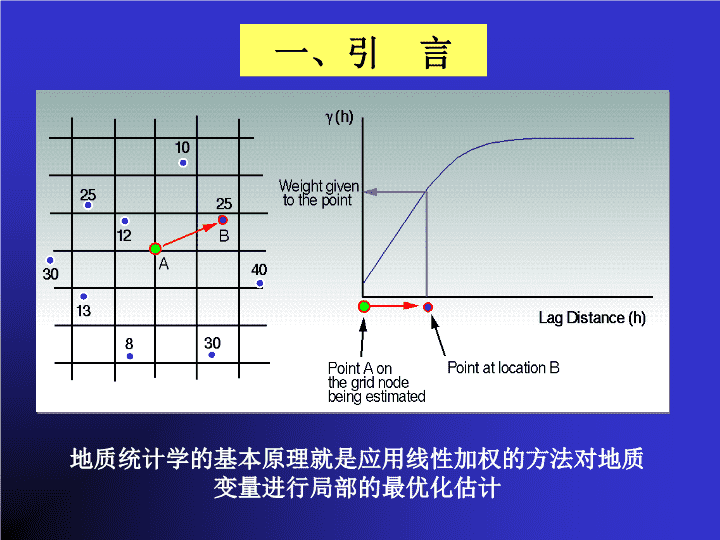
质统计学及其应用
地质统计学简介及其应用报告人:范崇海\n一、引言二、克里金算法介绍三、变差函数分析简介四、一个应用实例五、总结地质统计学简介及基本分析方法\n地质统计学的基本原理就是应用线性加权的方法对地质变量进行局部的最优化估计一、引言\n二、克里金算法介绍克里金算法是一类统计方法,就是估算一个数据场中任意一点的值的方法。前提条件是:相邻数据点的数值在空间中是相关的。且统计数据要达到一定的数量。主要优点是:考虑了数据场的方向性。其核心是:寻找到相邻数据点对所求点的权。\n常用的几种克里金算法1、简单克里金(SimpleKriging)2、普通克里金(OrdinaryKriging)3、非稳态克里金(NostationaryKriging)4、内在趋势克里金(UniversalKriging)(泛克里金)5、外在趋势克里金(KrigingwithanExternalDrift)6、同位协克里金(CollocatedCokriging)二、克里金算法介绍\n1、简单克里金(SimpleKriging)权系数的确定均值\n假定整个域的平均值为常数;远离数据点处接近平均值;网格点有数则为原值。简单克里金\n2、普通克里金(OrdinaryKriging)权系数的确定\n普通克里金普遍采用于成图的算法;远离数据点的值是寻找范围内的数据点的平均值。\n3、非稳态克里金(NostationaryKriging)\n非稳态克里金比较灵活的克里金算法,因为可以设置网格点的值;网格点的平均值来自于大范围的数据,而成图区只是一部分。\n4、内在趋势克里金(UniversalKriging)\n内在趋势克里金算法中权的确定\n内在趋势克里金如果是数据点的内插值,与普通克里金的精度相似;如果是外推计算,则需要用内在趋势克里金把握外推趋势。\n5、外在趋势克里金(KrigingwithanExternalDrift)\n外在趋势克里金算法中权的确定\n外在趋势克里金一般用于两组数据共同约束同一个地质解释时;例如做一个层的构造图,可用井数据作为硬指标而地震解释作为软指标,共同绘制构造图。\n6、同位协克里金(CollocatedCokriging)\n同位协克里金算法中权的确定\n同位协克里金同样用两组数据,约束一个参数,但是主要数据与辅助数据要有一定的相关性;例如用井点的孔隙度与地震属性数据,估算井间孔隙度。\n几种克里金算法之间的关系简单克里金非稳态克里金同位协克里金(Simple)(Nostationary)(CollocatedCokriging)普通克里金内在趋势克里金外在趋势克里金(Ordinary)(Universal)(WithanExternalDrift)\n克里金算法的核心权\n三、变差函数分析简介一般可通过统计和图形方法分析和确定空间相关性。实际分析数据的变化性称为变差函数分析。h-散点图变差函数图通过拟和一条连续的曲线,产生变差函数模型,最终确定出克里金算法中合理的加权方法。\n基本理论介绍:滞后距(Lag)变差函数分析实际是确定数据在方向和距离两方面的变化率尾头\n散点图\n半变差函数\n半变差函数图的构成\n变差函数图中各部分的名称基台跃迁变程\n变差函数图的构图机理\n变差函数图半变差函数H-散点图关系\n二维变差函数模型主轴变差图附轴变差图\n三维变差函数模型\n组成变差函数模型的结构类型跃迁球型高斯指数幂函数\n变差模型结构半变差函数滞后距\n四、一个应用实例---应用三维属性数据建立砂体模型三维属性数据\n数据分析、变差函数模型的建立、克里金计算\n砂体的三维模型\n精度比较\n储层富集带一定深度范围内储层的迭合厚度\n\n\n\n简单克里金算法中权的确定\n普通克里金算法中权的确定\n简单普通非稳同位协内在外在六类克里金算法的效果\n五、总结地质离散数据地质统计学分析变差函数分析变差函数模型克里金计算H散点图变差函数图简单克里金普通克里金非稳态克里金内在趋势克里金外在趋势克里金同位协克里金结果\n加大应用地质统计学的力度,提高油藏描述的准确性一、地质参数的估算-----井间的各类油藏参数的确定二、储层的非均质性研究-----发展随机建模技术三、综合应用各类地质资料-----特别是测井地质参数与地震属性的结合1、测井约束地震反演中初始模型的建立2、反演过程中加入地质统计技术查看更多