- 2022-08-29 发布 |
- 37.5 KB |
- 31页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
统计学实验excel实习
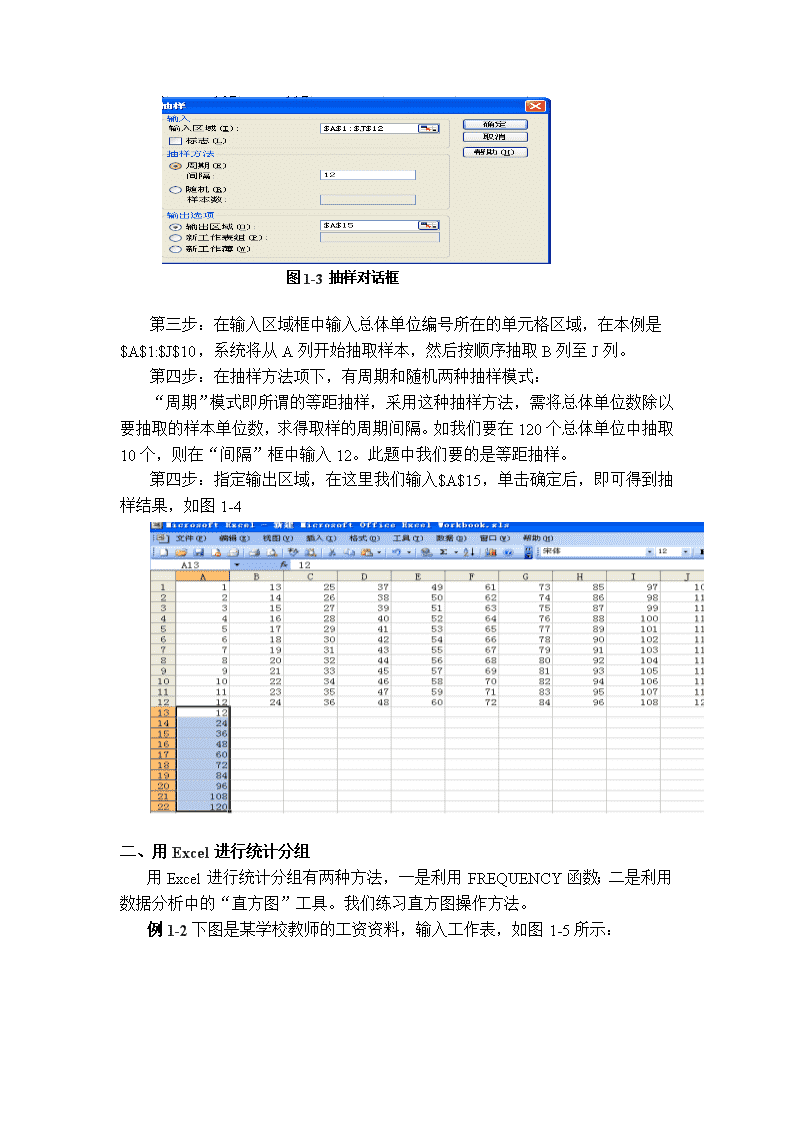
统计学实验Excel实习学院:经济与管理学院\n实验一Excel基本操作(用Excel搜集与整理数据)实验目的:掌握用EXCEL进行数据的搜集整理和显示实验步骤:一、用Excel搜集数据例1-1假定一个复读班有120个学生,即120个总体单位,每个总体单位给一个编号,共有从1到120个编号,输入工作表后如图1-1所示:图:1-1总体各单位编号表输入各总体单位的编号后,可按以下步骤操作:第一步:单击工具菜单,选择数据分析选项(若无数据分析选项,可在工具菜单下选择加载宏,在弹出的对话框中选择分析工具库,便可出现数据分析选项),打开数据分析对话框,从中选择抽样。如图1-2所示:图1-2数据分析对话框第二步:单击抽样选项,弹出抽样对话框。如图1-3\n图1-3抽样对话框第三步:在输入区域框中输入总体单位编号所在的单元格区域,在本例是$A$1:$J$10,系统将从A列开始抽取样本,然后按顺序抽取B列至J列。第四步:在抽样方法项下,有周期和随机两种抽样模式:“周期”模式即所谓的等距抽样,采用这种抽样方法,需将总体单位数除以要抽取的样本单位数,求得取样的周期间隔。如我们要在120个总体单位中抽取10个,则在“间隔”框中输入12。此题中我们要的是等距抽样。第四步:指定输出区域,在这里我们输入$A$15,单击确定后,即可得到抽样结果,如图1-4二、用Excel进行统计分组用Excel进行统计分组有两种方法,一是利用FREQUENCY函数;二是利用数据分析中的“直方图”工具。我们练习直方图操作方法。例1-2下图是某学校教师的工资资料,输入工作表,如图1-5所示:\n然后按以下步骤操作。第一步:在工具菜单中单击数据分析选项,从其对话框的分析工具列表中选择直方图,打开直方图对话框。如图1-6所示:图1-6直方图对话框第二步:在输入区域输入$A$1:$J$6,在接收区域输入$A$9:$A$6。接收区域指的是分组标志所在的区域,假定我们把分组标志输入到A9:A15单元格,注意这里只能输入每一组的上限值,即2000,2600,3200,3800,8000第三步:选择输出选项,可选择输入区域、新工作表组或新工作薄。本例为A8。第四步:选择图表输出,可以得到直方图;选择累计百分率,系统将在直方图上添加累积频率折线;选择柏拉图,可得到按降序排列的直方图。第五步:按确定按钮,可得输出结果如图1-7:\n应当注意,上图实际上是一个条形图,而不是直方图,若要把它变成直方图,可按如下操作:用鼠标左键单击任一直条,然后右键单击,在弹出的快捷菜单中选取数据系列格式,弹出数据系列格式对话框,如图1-8所示:在对话框中选择选项标签,把间距宽度改为0,按确定后即可得到直方图,如图1-9所示:\n图1-9调整后的直方图三、用Excel作统计图例1-3某学校2011级化工专业学生的年龄如下,首先把数据输入到工作表中,如图1-10所示:按以下步骤可作出饼图:第一步:选中某一单元格,单击插入菜单,选择图表选项,弹出图表向导对话框。如图1-11:\n第二步:在图表类型中选择饼图,然后在子图表类型中选择一种类型,这里我们选用系统默认的方式。然后单击下一步按钮,打开源数据对话框。如图1-12:图1-12源数据对话框第三步:在源数据对话框中填入数据所在区域,单击完成按钮,即可得如1-13\n所示的饼图:图1-13饼图从此图中我们可以看出:18岁的学生占19%,19岁的占18%,20岁的占17%,,21岁的占15%,22岁的占15%,23岁的占16%,由此可以得出,该班级学生的年龄比例基本差不多。\n实验二描述统计分析过程(用EXCEL计算描述统计量)实验目的:用EXCEL计算描述统计量实验步骤一.用函数计算描述统计量(一)众数【例1-4】:为了解某小学老师的的工资情况,随机抽取25人,月工资如下:2100,2200,2100,2300,2400,2200,2300,2500,2500,2400,2500,3000,3200,2300,2400,2500,3000,3600,4000,4500,5000,2100,1000,1200,1500用函数方法求众数,应先将30个人的工资数据输入A1:A25单元格,然后单击任一空单元格,输入“=MODE(A1:A25)”,回车后即可得众数为2500(二)中位数仍采用上面的例子,单击任一空单元格,输入“=MEDIAN(A1:A25)”,回车后得中位数为2400。(三)算术平均数单击任一单元格,输入“=AVERAGE(A1:A25)”,回车后得算术平均数为2548。(四)标准差单击任一单元格,输入“=STDEV(A1:A25)”,回车后得标准差为。703.0410135一、描述统计工具量的使用仍使用上面的例子,我们已经把数据输入到A1:A25单元格,然后按以下步骤操作:第一步:在工具菜单中选择数据分析选项,从其对话框中选择描述统计,按确定后打开描述统计对话框,如图1-14所示:图1-14描述统计对话框\n第二步:在输入区域中输入$A$1:$A$25,在输出区域中选择$C$6,其他复选框可根据需要选定,选择汇总统计,可给出一系列描述统计量;选择平均数置信度,会给出用样本平均数估计总体平均数的置信区间;第K大值和第K小值会给出样本中第K个大值和第K个小值,此题中K大值为2,小值为1.第三步:单击确定,可得输出结果,如图1-15所示:图1-15描述统计输出结果上面的结果中,平均指样本均值;标准误差指样本平均数的标准差;中值即中位数;模式指众数;标准偏差指样本标准差,自由度为n-1;峰值即峰度系数;偏斜度即偏度系数;区域实际上是极差或全距。\n实验三用EXCEL进行参数估计和假设检验实验目的:用EXCEL进行参数估计和假设检验实验步骤:一、用EXCEL进行区间估计例1-5:某中学校为了调查该校学生一天的消费情况,随机抽查了50个学生,则消费额(元)如下:10151112131415789101112131415111091011162025233329302520161213121313101067898751518131210求在概率90%的保证下,顾客平均消费额的估计区间。如图1-16:图1-16参数估计数据及结果计算方法如下:第一步:把数据输入到A2:A50单元格。第二步:在C2中输入公式“=COUNT(A2:A50)”,C3中输入“=AVERAGE(A2:A50)”,在C4中输入“STDEV(A2:A50)”,在C5中输入“=C4/SQRT(C2)”,在C6中输入0.90,在C7中输入“=C2-1”,在C8中输入“=TINV\n(1-C6,C7)”,在C9中输入“=C8*C5”,在C10中输入“=C3-C9”,在C11中输入“=C3+C9”。在输入每一个公式回车后,便可得到上面的结果,从上面的结果我们可以知道,顾客平均消费额的置信下限为12.24181214,置信上限为14.94186133关于总体方差的估计、总体比例的估计等可按类似方法进行。二、用EXCEL进行假设检验在EXCEL中,假设检验工具主要有四个,如图1-17所示:图1-17数据分析对话框平均值的成对二样本分析实际上指的是在总体方差已知的条件下两个样本均值之差的检验,准确的说应该是Z检验,双样本等方差检验是总体方差未知,但假定其相等的条件下进行的t检验,双样本异方差检验指的是总体方差未知,但假定其不等的条件下进行的t检验,双样本平均差检验指的是配对样本的t检验。我们介绍一下Z检验。例1-6:某班级为了比较甲,乙2名同学成绩,2人的各科成绩如下:甲(X)859096989088乙(Y)918789969995根据以往经验知成绩,,且,试在水平上比较成绩有无显著差别。计算步骤如下:第一步:输入数据到工作表。第二步:单击工具菜单,选择数据分析选项,弹出对话框后,在其中选择双样本平均差分析,弹出对话框如图1-18所示:\n图1-18双样本平均差分析对话框第三步:按上图所示输入后,按确定按钮,得输出结果如图1-19:图1-19双样本平均差分析结果在上面的结果中,我们可以根据P值进行判断,也可以根据统计量和临界值比较进行判断。如本例采用的是单尾检验,其单尾P值为0.07,大于给定的显著性水平0.05,所以应该接受原假设,即2人成绩没有明显差别;若用临界值判断,得出的结论是一样的,如本例Z值为—1.4433,小于临界值1.644853,由于是右尾检验,所以也是接受原假设\n实验四用EXCEL进行方差分析实验目的:学会在计算机上利用EXCEL进行单因素方差分析和有交互作用的双因素方差分析以及无交互作用双因素方差分析。实验步骤:一、单因素方差分析 用Excel进行方差分析时对数据格式有特殊的要求,不能使用我们前面学过的列表格式,而应使用一种特殊的表格形式:在单因素方差分析中因素的不同水平作为表格的列(或行),在不同水平下的重复次数作为行(或列);在双因素方差分析时以一个因素的不同水平作为列,以另一个因素以及试验的重复次数作为行。这种设计使得Excel最多只能进行两个因素的方差分析。例1-7:为了调查面试和录用率间的关系,试用方差分析的方法比较在5%的显著性水平下能否认为面试对录用率有显著影响。在Excel中,先对数据按面试排序,然后把统计成绩整理成表1-1的形式。从分组的结果看,在不同的因素水平下的观测个数并不相同。这种情况下的方差分析与等重复的方差分析原理完全相同,只是计算公式上稍有不同。当然使用统计软件进行计算时完全看不出这种影响。 在Excel的分析工具库中选择“方差分析:单因素方差分析”,指定相应的数据区域和显著性水平,点击“确定”后的输出结果如表1-2和1-3。 表1-2 单因素方差分析的汇总表 \n表1-2是各组数据的描述统计指标。从各组的均值看,录用率最低的为0.665,最高的为0.735。从各组的方差看最小的为0.01223,最大的等于0.2495。判断数据是否符合同方差假设的一个经验方法是:如果各组之中最大的方差与最小方差之间的比值不超过4,就可以认为是同方差的。在这个例子中比值为20.40065,可能违背了同方差的假设。 表1-3单因素方差分析的方差分析表 在这个例子中如果假设数据是同方差的,则方差分析的中得出的p-值等于0.855475大于0.05,因此应接受零假设,检验的结论是面试对录用率没有显著影响。注意在方差分析中的F检验是右侧检验,软件给出的p-值是单侧检验的p-值。\n 二、用Excel进行无重复双因素方差分析无重复的双因素方差分析可以同时分析两个因素对因变量的影响。下面我们来看一个简单的例子。例1-8:为了比较四个不同学校老师的收入设计了以下实验:从四个学校中,按教龄分为10个等级各等级选择一名老师进行调查,调查结果如表1-4。显著性水平α=0.01。试分析不同学校教师的收入有显著差异吗?教龄对收入有显著影响吗?1-4不同学校老师的月收入(元) 在Excel表格中输入相应的数据,从“数据分析”中选择“方差分析:无重复双因素分析”,在对话框中输入数据区域、显著性水平和输出方式,得到方差分析表如表1-5。从分析结果可以看出,行因素(学校)的p-值为1.09E-06,小于0.01,说明不同学校对老师的收入有显著性影响。列因素(教龄)的p-值为0.149985,大于0.01,说明教龄对老师的收入都有显著影响。 \n表1-5 无重复双因素方差分析表三、 用Excel进行有重复双因素方差分析与无重复的双因素方差分析不同,有重复的双因素方差分析可以分为有交互作用和无交互作用两种情况。Excel只能分析有交互作用的情况。例1-9:一家电脑公司在美国,英国,德国,中国四个国家销售大型电脑件、小型电脑,微型电脑,。为了比较不同国家三类电脑销售人员的收入,随机收集了一组数据(表1-6)。假设数据是正态的和等方差的。试在α=0.05的显著性水平下分析各因素及其交互作用的影响是否显著。 \n表1-6电脑销售人员的月收入数据(元) 在Excel表格中输入相应的数据,从“数据分析”中选择“方差分析:有重复双因素分析”,在对话框中输入数据区域、显著性水平和输出方式,并指明每种处理重复的次数(这里为3次)(图1-20)。注意在有重复双因素分析的“输入区域”中要包括行和列的分组状况,否则Excel会报错。最后得到的方差分析表如表1-7。从分析结果可以看出,样本因素(行因素,即产品类型)的p-值为0.001121,说明销售的电脑类型对销售人员的平均收入有显著差异;电脑列因素(专业)的p-值为0.00231,都远远小于0.01,可见两个因素对销售人员的收入都有显著影响;列因素(国家)的p-值为0.004051<0.05,说明国家因素对收入有显著影响;两个因素的交互作用的p-值为0.004588<0.05,说明二者的交互作用对销售人员的平均收入有显著影响。\n图1-20有重复双因素方差分析的对话框 表1-7有重复双因素方差分析表\n实验五用EXCEL进行时间序列分析实验目的:用EXCEL进行时间序列分析实验步骤:一、测定增长量和平均增长量例1-10:根据1991-2005年甘肃省国内生产总值,计算逐期增长量、累计增长量和平均增长量。如图1-21图1-21用EXCEL计算增长量和平均增长量资料及结果计算步骤如下:第一步:在A列输入年份,在B列输入国内生产总值。\n第二步:计算逐期增长量:在C3中输入公式:=B3-B2,并用鼠标拖曳将公式复制到C3:C16区域。第三步:计算累计增长量:在D3中输入公式:=B3-$B$2,并用鼠标拖曳公式复制到D3:D16区域。\n第四步:计算平均增长量(水平法):在C18中输入公式:=(B16-B2)/5,按回车键,即可得到平均增长量。二、测定发展速度和平均发展速度 例1-11:以1991-2005年甘肃省国内生产总值为例,说明如何计算定基发展速度、环比发展速度和平均发展速度。如图1-22\n图1-22用EXCEL计算发展速度和平均发展速度资料及结果第一步:在A列输入年份,在B列输入国内生产总值。第二步:计算定基发展速度:在C3中输入公式:=B3/$B$2\n,并用鼠标拖曳将公式复制到C3:C16区域。第三步:计算环比发展速度:在D3中输入公式:=B3/B2,并用鼠标拖曳将公式复制到D3:D16区域。\n第四步:计算平均发展速度(水平法):选中C18单元格,单击插入菜单,选择函数选项,出现插入函数对话框后,选择GEOMEAN(返回几何平均值)函数,在数值区域中输入D3:D8即可。三、计算长期趋势例1-12:我们用某国企2002年12个月的总产值资料来说明如何用移动平均法计算长期趋势。如图1-23图1-23用EXCEL计算长期趋势资料及结果第一步:在A列输入月份,在B列输入总产值。\n第二步:计算三项移动平均:在C3中输入“=(B2+B3+B4)/3”,并用鼠标拖曳将公式复制到C3:C12区域。第三步:计算四项移动平均:在D4中输入“=SUM(B2:B5)/4”,并用鼠标拖曳将公式复制到D4:D12区域。\n第四步:计算二项移正平均数:在E4中输入“=(D4+D5)/2”,并用公式拖曳将公式复制到E4:E11区域。 四、计算季节变动 例1-13:利用红星工厂五年分季度消耗原材料总额的资料,说明如何用移动平均趋势剔除法测定季节变动。如图1-24\n图1-24用EXCEL计算季节变动资料第一步:按图上的格式在A列输入年份,在B列输入季别,在C列输入消耗原材料的总额。\n第二步:计算四项移动平均:在D3中输入“=SUM(C2:C4)/4”,并用鼠标拖曳将公式复制到D3:D19区域。\n第三步:计算趋势值(即二项移动平均)T:在E4中输入“=(D3+D4)/2”,并用鼠标拖曳将公式复制到E4:E19区域。第四步:剔除长期趋势,即计算Y/T:在F4中输入“=C4/E4”,并用鼠标拖曳将公式复制到F4:F19区域。\n第五步:重新排列F4:F19区域中的数字,使同季的数字位于一列,共排成四列。第六步:计算各年同季平均数:在B29单元格中输入公式:=average(B25:B28);在C29中输入公式=average(C25:C28);在D29中输入公式=average(D24:27);在E29中输入公式=average(E24:E27)。第七步:计算调整系数:在B31中输入公式:=4/sum(B29:E29)第八步:计算季节比率:在B30中输入公式:=B29*$B$31,并用鼠标拖曳将公式复制到单元格区域B30:E30,就可以得到季节比率的值,具体结果见图1-25:图1-25用EXCEL计算季节变动结果查看更多