- 2022-08-24 发布 |
- 37.5 KB |
- 51页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
统计学概率ppt课件
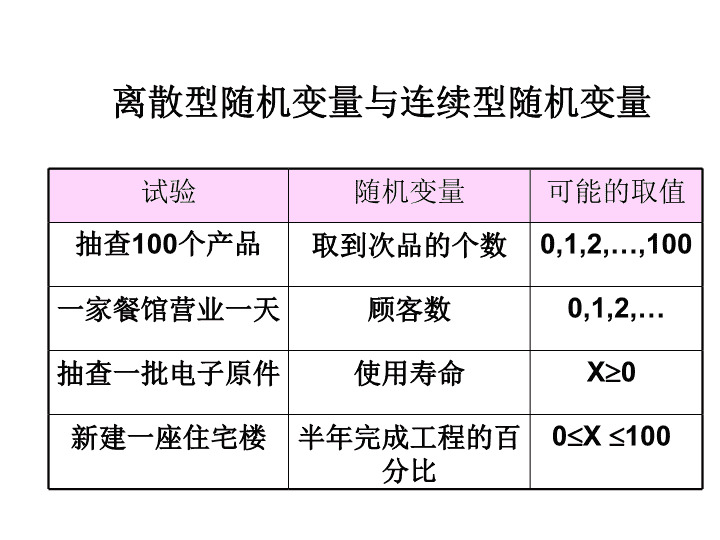
第4章随机变量的概率分布4.4离散随机变量的分布4.5连续随机变量的分布4.6使用概率来检验假设\n学习目标离散随机变量及相应的分布连续随机变量及相应的分布;利用概率进行决策分析。\n离散型随机变量与连续型随机变量试验随机变量可能的取值抽查100个产品取到次品的个数0,1,2,…,100一家餐馆营业一天顾客数0,1,2,…抽查一批电子原件使用寿命X0新建一座住宅楼半年完成工程的百分比0X100\n分布随机变量取一切可能值或范围的概率或概率的规律称为概率分布(probabilitydistribution,简称分布)。概率分布可以用各种图或表来表示;一些可以用公式来表示。概率分布是关于总体的概念。有了概率分布就等于知道了总体。前面介绍过的样本均值、样本标准差和样本方差等样本特征的概念是相应的总体特征的反映。我们也有描述变量“位置”的总体均值、总体中位数、总体百分位数以及描述变量分散(集中)程度的总体标准差和总体方差等概念。\n4.4离散随机变量的分布离散变量只取离散的值,比如骰子的点数、网站点击数、顾客人数等等。每一种取值都有某种概率。各种取值点的概率总和应该是1。当然离散变量不不仅仅限于取非负整数值。一般来说,某离散随机变量的每一个可能取值xi都相应于取该值的概率p(xi),这些概率应该满足关系\n最简单的离散分布应该是基于可重复的有两结果(比如成功和失败)的相同独立试验(每次试验成功概率相同)的分布,例如抛硬币。比如用p代表得到硬币正面的概率,那么1-p则是得到反面的概率。如果知道p,这个抛硬币的试验的概率分布也就都知道了。4.4.1二项分布\n这种有两个可能结果的试验有两个特点:一是各次试验互相独立,二是每次试验得到一种结果的概率不变(这里是得到正面的概率总是p)。类似于抛硬币的仅有两种结果的重复独立试验被称为贝努里试验(Bernoullitrials)。4.4.1二项分布\n下面试验可看成为贝努里试验:每一个进入某商场的顾客是否购买某商品每个被调查者是否认可某种产品每一个新出婴儿的性别。根据这种简单试验的分布,可以得到基于这个试验的更加复杂事件的概率。为了方便,人们通常称贝努里试验的两种结果为“成功”和“失败”。4.4.1二项分布\n和贝努里试验相关的最常见的问题是:如果进行n次贝努里试验,每次成功的概率为p,那么成功k次的概率是多少?这个概率的分布就是所谓的二项分布(binomialdistribution)。这个分布有两个参数,一个是试验次数n,另一个是每次试验成功的概率p。基于此,二项分布用符号B(n,p)或Bin(n,p)表示。由于n和p可以根据实际情况取各种不同的值,因此二项分布是一族分布,族内的分布以这两个参数来区分。4.4.1二项分布\n一般公式。下面p(k)代表在n次Bernoulli试验中成功的次数的概率,p为每次试验成功的概率。有这里为二项式系数,或记为4.4.1二项分布\n九个二项分布B(5,p)(p=0.1到0.9)的概率分布图\n另一个常用离散分布是Poisson分布(“泊松分布”)。它可以认为是衡量某种事件在一定期间出现的数目的概率。比如说在一定时间内顾客的人数、打入电话总机电话的个数、页面上出现印刷错误的个数、纺织品上出现疵点的个数。4.4.2Poisson分布\n在不同条件下,同样事件在单位时间中出现同等数目的概率不尽相同。比如中午和晚上某商店在10分钟内出现5个顾客的概率就不一定相同。因此,Poisson分布也是一个分布族。族中不同成员的区别在于事件出现数目的均值l不一样。4.4.2Poisson分布\n参数为l的Poisson分布变量的概率分布为(p(k)表示Poisson变量等于k的概率)4.4.2Poisson分布\n参数为3、6、10的Poisson分布(只标出了20之内的部分)这里点间的连线没有意义,仅仅为容易识别而画,因为Poisson变量仅取非负整数值\n假定有一批500个产品,而其中有5个次品。假定该产品的质量检查采取随机抽取20个产品进行检查。如果抽到的20个产品中含有2个或更多不合格产品,则整个500个产品将会被退回。这时,人们想知道,该批产品被退回的概率是多少?这种概率就满足超几何分布(hypergeometricdistribution)。4.4.3超几何分布\n取连续值的变量,如高度、长度、重量、时间、距离等等;它们被称为连续变量(continuousvariable)。换言之,一个随机变量如果能够在一区间(无论这个区间多么小)内取任何值,则该变量称为在此区间内是连续的,其分布称为连续型概率分布。它们的概率分布很难准确地用离散变量概率的条形图表示。4.5连续变量的分布\n想象连续变量观测值的直方图;如果其纵坐标为相对频数,那么所有这些矩形条的高度和为1;完全可以重新设置量纲,使得这些矩形条的面积和为1。不断增加观测值及直方图的矩形条的数目,直方图就会越来越像一条光滑曲线,其下面的面积和为1。该曲线即所谓概率密度函数(probabilitydensityfunction,pdf),简称密度函数或密度。下图为这样形成的密度曲线。4.5连续变量的分布\n逐渐增加矩形条数目的直方图和一个形状类似的密度曲线。\n连续变量落入某个区间的概率就是概率密度函数的曲线在这个区间上所覆盖的面积;因此,理论上,这个概率就是密度函数在这个区间上的积分。对于连续变量,取某个特定值的概率都是零,而只有变量取值于某个(或若干个)区间的概率才可能大于0。连续变量密度函数曲线(这里用f表示)下面覆盖的总面积为1,即4.5连续变量的分布\n4.5.1均匀分布均匀分布(uniformdistribution)是最简单的连续型分布。它的取值范围是一个区间,比如(a,b)。均匀分布随机变量X取值在该区间的一个子区间的概率等于该子区间宽度与区间(a,b)宽度b-a之比,例如,假设区间(a,b)为(0,1)区间,那么X落入(0.2,0.5)的概率为(0.5-0.2)/(1-0)=0.3。\n4.5.1均匀分布下图展示了在区间(0,1)上的均匀分布的密度函数。\n近似地服从正态分布(normaldistribution,又叫高斯分布,Gaussiandistribution)。的变量很常见,象测量误差、商品的重量或尺寸、某年龄人群的身高和体重等等。在一定条件下,许多不是正态分布的样本均值在样本量很大时,也可用正态分布来近似。4.5.2正态分布\n正态分布的密度曲线是一个对称的钟型曲线(最高点在均值处)。正态分布也是一族分布,各种正态分布根据它们的均值和标准差不同而有区别。一个正态分布用N(m,s2)表示;其中m为均值,而s2为方差(标准差的平方)。也常用N(m,s)来表示,这里s为标准差。4.5.2正态分布\n哈佛大学心理学家RichardJ.Herrrnstein和美国企业研究所(AmericanEnterpriseInstitute)著名学者CharlesMurray的名著《钟曲线:美国生活中的智商与阶级结构》智商是天生的,和家庭背景、阶层、甚至教育程度都没有关系。高智商和低智商在人口中的分布,长期以来基本是固定的。高智商的人反正都会成功,于是就集中资源对低智商的人进行倾斜性的教育投资,这违反了基本的市场逻辑。智商和阶层没有关系,有钱的人未必智商高。4.5.2正态分布\n标准差为1的正态分布N(0,1)称为标准正态分布(standardnormaldistribution)标准正态分布的密度函数用f(x)表示。任何具有正态分布N(m,s2)的随机变量X都可以用简单的变换(减去其均值m,再除以标准差s):Z=(X-m)/s,而成为标准正态随机变量。这种变换和标准得分的意义类似。4.5.2正态分布\n两条正态分布的密度曲线。左边是N(-2,0.52)分布,右边是N(0,1)分布\n当然,和所有连续变量一样,正态变量落在某个区间的概率就等于在这个区间上,密度曲线下面的面积。比如,标准正态分布变量落在区间(0.51,1.57)中的概率,就是在标准正态密度曲线下面在0.51和1.57之间的面积。很容易得到这个面积等于0.24682;也就是说,标准正态变量在区间(0.51,1.57)中的概率等于0.24682。如果密度函数为f(x),那么这个面积为积分4.5.2正态分布\n标准正态变量在区间(0.51,1.57)中的概率\n对于连续型随机变量X,a下侧分位数(又称为a分位数,a-quantile)定义为数xa,它满足关系这里的a又称为下(左)侧尾概率(lower/lefttailprobability)4.5.2正态分布\n而a上侧分位数(又称a上分位数,a-upperquantile)定义为数xa,它满足关系这里的a也称为上(右)侧尾概率(upper/righttailprobability)。4.5.2正态分布\n通常用za表示标准正态分布的a上侧分位数,即对于标准正态分布变量Z,有P(Z>za)=a。下图表示了0.05上侧分位数za=z0.05及相应的尾概率(a=0.05)。有些书用符号z1-a而不是za;因此在看参考文献时要注意符号的定义。4.5.2正态分布\nN(0,1)分布右侧尾概率P(z>za)=a的示意图\n【例】某厂生产的某种节能灯管的使用寿命服从正态分布,对某批产品测试的结果,平均使用寿命为1050小时,标准差为200小时。试求:(a)使用寿命在500小时以下的灯管占多大比例?(b)使用寿命在850~1450小时的灯管占多大比例?(c)以均值为中心,95%的灯管的使用寿命在什么范围内?\n解X=使用寿命,X~N(1050,2002)=Ф(2)-Ф(-1)=0.97725-0.15865=0.818695%的灯管寿命在均值左右392(即658~1442)小时=1-Ф(2.75)=1-0.99702=0.00298\n正态变量的样本均值也是正态变量,能利用减去其均值再除以其(总体)标准差来得到标准正态变量。但用样本标准差来代替未知的总体标准差时,得到的结果分布就不再是标准正态分布了。它的密度曲线看上去有些象标准正态分布,但是中间瘦一些,而且尾巴长一些。这种分布称为t-分布(t-distribution,或学生分布,Student’st)。4.5.3t-分布\n不同的样本量通过标准化所产生的t分布也不同,这样就形成一族分布。t分布族中的成员是以自由度来区分的。这里的自由度等于样本量减去1(如果样本量为n,刚才定义的t分布的自由度为n-1)。由于产生t分布的方式很多,简单说自由度就是样本量减1是不准确的。自由度甚至不一定是整数。4.5.3t-分布\n标准正态分布和t(1)分布的密度图\n通常用ta表示t分布相应于右侧尾概率a的t变量的a上侧分位数,即对于t分布变量T,有P(T>ta)=a。在突出自由度时,也用tn,a,也有用t1-a或tn,1-a表示的。下图表示了自由度为2的t(2)分布右边的尾概率(a=0.05)。4.5.3t-分布\nt(2)分布右侧尾概率P(t>ta)=a的示意图\n一个由正态变量导出的分布是c2-分布(chi-squaredistribution,也翻译为卡方分布)。该分布在一些检验中会用到。n个独立正态变量平方和称为有n个自由度的c2-分布,记为c2(n)。c2-分布为一族分布,成员由自由度区分。由于c2-分布变量为正态变量的平方和,它不会取负值。4.5.4c2-分布\n自由度为2、3、5的c2-分布密度曲线图\nF-分布变量为两个c2-分布变量(在除以它们各自自由度之后)的比;而两个c2-分布的自由度则为F-分布的自由度,因此,F-分布有两个自由度;第一个自由度等于在分子上的c2-分布的自由度,第二个自由度等于在分母的c2-分布的自由度。4.5.5F-分布\n自由度为(3,20)和(50,20)的F-分布密度曲线图\n判明一个事情的真伪,需要用事实说话。在统计中事实总是来源于数据。假定某药厂声称该厂生产的某种药品有60%的疗效。但是当实际调查了100名使用该药物的患者之后,发现有40名患者服后有效。这个数据是否支持药厂的说法呢?药厂所支持的模型实际上是一个参数为0.6的Bernoulli试验模型。100名患者的服药,实际上等于进行了100次试验。这就是二项分布B(100,0.6)模型。4.6使用概率来检验假设\n由于使用了药厂的0.6成功概率。这个模型是基于药厂的观点的。可以基于这个模型计算100名患者中有少于或等于40名患者治疗有效的概率。通过计算(或查表,后面会详细描述)易得,在药厂观点正确的假定下,这个概率为0.000042。这说明,如果药厂正确,那么只有40名患者有效这个事实是个小概率事件,即“少于或等于40名患者有效”的可能性只有大约十万分之四。4.6使用概率来检验假设\n这样在药厂的观点和事实之间有了矛盾。是事实准确还是药厂准确呢?显然人们一般不会认为药厂的说法可以接受。这样,就利用小概率事件来拒绝了药厂的说法。这种用小概率事件对假定的模型进行判断是后面要介绍的假设检验的基础。4.6使用概率来检验假设\n练习题1、抛掷一枚均匀硬币120次,求下列事件发生的概率: (1)出现正面次数占40%到60%(2)出现正面次数占5/8或更多2、有500个人,每人抛掷一枚均匀硬币120次,预计有多少人能得到(1)出现正面次数占40%到60%(2)出现正面次数占5/8或更多\n3、已知某台机器生产的产品中有2%是次品,现有400个这样的工具,求下列事件发生的概率:(1)次品不少于3%(2)次品不多于2%\n4、某此选举结果表明某一位候选人得到了46%的选票,从选民中随机抽取一些人作民意测验,求大多数人支持这位候选人的概率: (1)选取200个人 (2)选取1000个人\n此课件下载可自行编辑修改,供参考!感谢您的支持,我们努力做得更好!查看更多