- 2022-08-24 发布 |
- 37.5 KB |
- 99页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
第04章管理统计学
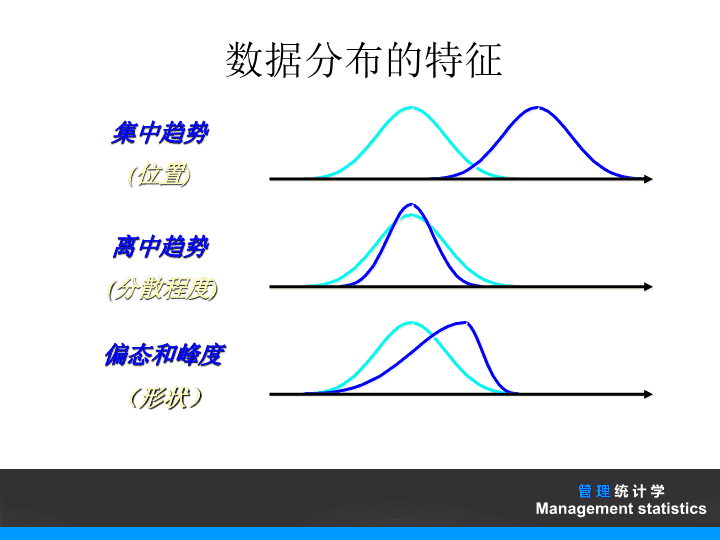
管理统计学Managementstatistics第四章描述统计中的测度\n管理统计学Managementstatistics1.集中趋势2.离散趋势3.统计数据的来源3.分布形状目录\n数据分布的特征集中趋势(位置)离中趋势(分散程度)偏态和峰度(形状)管理统计学Managementstatistics\n数据的特征和度量集中趋势算术平均数调和平均数几何平均数中位数众数百分位数四分位数离散趋势极差四分位距平均差方差与标准差标准分数离散系数分布形状偏态测度峰态测度管理统计学Managementstatistics\n4.1数据分布的集中趋势测度集中趋势(generaltendency)是指分布的定位,它是指一组数据向某一中心值靠拢的倾向,或是表明一组统计数据所具有的一般水平。集中趋势测度数值平均数算术平均数调和平均数几何平均数众数百分位数四分位数位置平均数中位数管理统计学Managementstatistics\n集中趋势(Centraltendency)一组数据向其中心值靠拢的倾向和程度测度集中趋势就是寻找数据一般水平的代表值或中心值不同类型的数据用不同的集中趋势测度值低层次数据的集中趋势测度值适用于高层次的测量数据,反过来,高层次数据的集中趋势测度值并不适用于低层次的测量数据选用哪一个测度值来反映数据的集中趋势,要根据所掌握的数据的类型来确定管理统计学Managementstatistics\n4.1.1数值平均数数值平均数又称均值(mean)根据统计资料的数值计算而得到,在统计学中具有重要的作用和地位,是度量集中趋势的最主要的指标之一。平均的对象可理解为变量,平均数可记为。管理统计学Managementstatistics\n1.算术平均数1)简单算术平均数简单算术平均数是根据原始数据直接计算均值。一般地,设一组数据为,其简单算术平均数计算的一般公式可表达为:管理统计学Managementstatistics\n简单均值(算例)原始数据:10591368\n例:为了研究目前大学中班级学生人数的情况,从北京某大学抽样五个班级,其学生人数分别为:46,54,42,46,32。我们使用,…分别表示该五个数据,计算其均值,可以写成:算术平均数管理统计学Managementstatistics\n2)加权算术平均数加权算术平均数计算的所依靠的数据是经过一定整理的,即是根据一定规则分组的。可分为:(1)由数列计算加权算术平均数(2)根据组距计算加权算术平均数算术平均数管理统计学Managementstatistics\n(1)由数列计算加权算术平均数由单项变量数列计算加权算术平均数的基础是要先将数据进行分组,即将n个数据按变量值(xi)进行分组,并统计在各个变量取值出现的次数,或称为频数(fi)。其加权算术平均数的计算公式如下:算术平均数管理统计学Managementstatistics\n设某班级10名同学的年龄分别为:18,19,17,18,17,18,19,18,18,19。则根据简单平均数的公式,我们可计算得到该班10名同学的平均年龄:算术平均数管理统计学Managementstatistics\n1722/10(0.2)1866/10(0.6)1922/10(0.2)合计101年龄(岁)人数人数比重算术平均数\n(2)根据组距计算加权算术平均数选择适当的组距来对数据进行分组,再求加权平均数往往就简单、容易许多。根据组距计算加权平均数的方法与上面所述的数列加权平均数方法基本相同,只需以各组的组中值来代替相应的x值即可。算术平均数管理统计学Managementstatistics\n加权均值表4-1某车间50名工人日加工零件均值计算表按零件数分组组中值(Xi)频数(Fi)XiFi105~110110~115115~120120~125125~130130~135135~140107.5112.5117.5122.5127.5132.5137.5358141064322.5562.5940.01715.01275.0795.0550.0合计—506160.0【例4.7】根据第三章表3-5中的数据,计算50名工人日加工零件数的均值管理统计学Managementstatistics\n①简单算术平均数适用于数据量较少的未分组数据;加权算术平均数则只适用于分组数据,且在进行数据分组时,可以根据每个变量的取值来分组,亦或根据一定的区间来分组,这应该根据所针对问题的具体数据来来选取。②简单算术平均数其数值的大小只与变量值的大小有关;对最终加权平均数大小的影响因素有两个:一是各组变量值的影响;另一个是各组变量值的频数的影响。算术平均数管理统计学Managementstatistics\n③加权算术平均数计算公式中频数的大小起着重要作用,当变量值比较大的次数多时,平均数就接近变量值大的一方;当变量值比较小的次数多时,平均数就接近于变量值小的一方。可见,次数对变量值在平均数中的影响起着某种权衡轻重的作用,因此被称为权数。④在加权算术平均数计算中当各组变量的权重相等时,则权重的权衡轻重的作用也就消失了,此时加权算术平均数转化为简单算术平均数的计算形式。算术平均数管理统计学Managementstatistics\n调和平均数(harmonicmean)是均值的另一种重要表示形式,由于它是根据变量值倒数计算的,也叫倒数平均数,一般用字母表示Hm。根据所给资料情况的不同,调和平均数可分为:简单调和平均数和加权调和平均数两种。调和平均数管理统计学Managementstatistics\n1.简单调和平均数事实上简单调和平均数是权数均相等条件下的加权调和平均数的特例。当权数相等时,就产生了通常所说的加权调和平均数。调和平均数管理统计学Managementstatistics\n2.加权调和平均数用公式表示为:由此可以看出,当权重mi相等时,则加权调和平均数则转换为简单调和平均数。调和平均数管理统计学Managementstatistics\n3.调和平均数是算术平均数的变形在一定的条件下,加权调和平均数和加权算术平均数只是计算形式不同,在经济内容上没有实质性的区别,调和平均数是算术平均数的变形,是在缺少总体单位的资料时才被迫使用的计算平均数的一种方法。即调和平均数管理统计学Managementstatistics\n调和平均数表4-3某日三种蔬菜的批发成交数据蔬菜名称批发价格(元)Xi成交额(元)XiFi成交量(公斤)Fi甲乙丙1.200.500.801800012500640015000250008000合计—3690048000【例4.8】某蔬菜批发市场三种蔬菜的日成交数据如表4-2,计算三种蔬菜该日的平均批发价格管理统计学Managementstatistics\n几何平均数(geometricmean)几何平均数是变量值连乘积的次方根,常用字母表示。它是平均指标的另一种计算形式。几何平均数是计算平均比率和平均速度最适用的一种方法。根据掌握的数据资料不同,几何平均数可分为简单几何平均数和加权几何平均数两种。几何平均数管理统计学Managementstatistics\n1.简单几何平均数假定有n个变量值x1,x2,……xn,则简单几何平均数的基本计算公式为:几何平均数管理统计学Managementstatistics\n2.加权几何平均数当掌握的数据资料为分组资料,且各个变量值出现的次数不相同时,应用加权方法计算几何平均数。加权几何平均数的公式为:几何平均数管理统计学Managementstatistics\n几何平均数【例】一位投资者持有一种股票,1996年、1997年、1998年和1999年收益率分别为4.5%、2.0%、3.5%、5.4%。计算该投资者在这四年内的平均收益率。平均收益率=103.84%-1=3.84%管理统计学Managementstatistics\n数值平均数根据所提供资料的具体数值计算而得到,和我们通常观念中的平均含义比较接近,但结果受极端值的影响而不能真是地反应改组资料的整体集中趋势,在这种情况下,一般可以考虑用位置中位数取代算术中位数来对数据的集中趋势进行描述。常用的位置平均数有:平均数、众数、分位数。二、位置平均数管理统计学Managementstatistics\n中位数(median)度量数据集中趋势的另一重要测度,它是一组数据按数值的大小从小到大排序后,处于中点位置上的变量值。通常用表示Me。定义表明,中位数就是将某变量的全部数据均等地分为两半的那个变量值。其中,一半数值小于中位数,另一半数值大于中位数。中位数是一个位置代表值,它不受极端变量值影响。中位数管理统计学Managementstatistics\n1.根据未分组数据确定中位数对于未分组的数据,确定其中位数的具体步骤为:(1)将变量按变量值大小从小到大进行排列。(2)确定中位数的位置,即中点位置。一般的,设一组数据的个数为,则中点的位置为(n+1)/2。(3)确定中位数。Me50%50%中位数管理统计学Managementstatistics\n如果观测值的数目n为奇数,则(n+1)/2为整数,该位置上所对应的变量即为所求的中位数。如果观测值的数目n为偶数,则(n+1)/2为非整数,则取位于中间位置的两个变量值的算术平均数作为中位数。中位数管理统计学Managementstatistics\n2.根据单项数列确定中位数根据单项数列资料确定中位数与根据未分组资料确定中位数方法基本一致。具体步骤为:(1)计算各组的累计次数(或频数)(2)确定中位数的位置,k=。(3)确定中位数。中位数所在组的变量值即为中位数。中位数管理统计学Managementstatistics\n3.根据组距数列确定中位数如果我们掌握的资料是分组后得到的组距数列,则确定中位数的步骤为:(1)确定中位数的位置,k=。(2)计算累计次数,据以找出中位数所在的组。(3)利用以下公式,确定中位数的近似值中位数管理统计学Managementstatistics\n中位数\n定序数据的中位数【例】根据第三章表3-2中的数据,计算甲城市家庭对住房满意状况评价的中位数解:中位数的位置为:300/2=150从累计频数看,中位数的在“一般”这一组别中。因此Me=一般表3-2甲城市家庭对住房状况评价的频数分布回答类别甲城市户数(户)累计频数非常不满意不满意一般满意非常满意2410893453024132225270300合计300—管理统计学Managementstatistics\n数值型未分组数据的中位数(5个数据的算例)原始数据:2422212620排序:2021222426位置:12345中位数22管理统计学Managementstatistics\n数值型未分组数据的中位数(6个数据的算例)原始数据:10591268排序:56891012位置:123456位置N+126+123.5中位数8+928.5管理统计学Managementstatistics\n根据位置公式确定中位数所在的组采用下列近似公式计算:4.该公式假定中位数组的频数在该组内均匀分布数值型分组数据的中位数(要点及计算公式)管理统计学Managementstatistics\n数值型分组数据的中位数表3-5某车间50名工人日加工零件数分组表按零件数分组频数(人)累积频数105~110110~115115~120120~125125~130130~135135~140358141064381630404650合计50—【例】根据第三章表3-5中的数据,计算50名工人日加工零件数的中位数管理统计学Managementstatistics\n众数(mode)一组数据中出现次数最多的那个变量值,通常用MO表示。如果在一个总体当中,各变量值皆不相同,或各个变量值出现的次数皆相同,则没有众数。如果在一个总体中,有两个标志值出现的次数都最多,称为双众数。只有在总体单位比较多、变量值有明显集中趋势的条件下确定的众数,才能代表总体的一般水平;在总体单位较少,或虽多但无明显集中趋势的条件下,众数的确定是没有意义的。众数的确定方法要根据给定资料的具体情况而定。众数管理统计学Managementstatistics\n1.未分组资料或单项数列资料众数观察给定的数据,某个变量出现次数最多,则该变量即为所求众数。这样的方法确定比较容易,不需要计算。众数管理统计学Managementstatistics\n2.根据组距变量数量确定众数具体步骤为:众数\n众数(概念要点)集中趋势的测度值之一出现次数最多的变量值不受极端值的影响可能没有众数或有几个众数主要用于定类数据,也可用于定序数据和数值型数据管理统计学Managementstatistics\n众数(众数的不唯一性)无众数原始数据:10591268一个众数原始数据:659855多于一个众数原始数据:252828364242管理统计学Managementstatistics\n定类数据的众数(算例)表3-1某城市居民关注广告类型的频数分布广告类型人数(人)比例频率(%)商品广告服务广告金融广告房地产广告招生招聘广告其他广告112519161020.5600.2550.0450.0800.0500.01056.025.54.58.05.01.0合计2001100【例】根据第三章表3-1中的数据,计算众数解:这里的变量为“广告类型”,这是个定类变量,不同类型的广告就是变量值。我们看到,在所调查的200人当中,关注商品广告的人数最多,为112人,占总被调查人数的56%,因此众数为“商品广告”这一类别,即Mo=商品广告管理统计学Managementstatistics\n定序数据的众数(算例)【例】根据第三章表3-2中的数据,计算众数解:这里的数据为定序数据。变量为“回答类别”。甲城市中对住房表示不满意的户数最多,为108户,因此众数为“不满意”这一类别,即Mo=不满意表3-2甲城市家庭对住房状况评价的频数分布回答类别甲城市户数(户)百分比(%)非常不满意不满意一般满意非常满意24108934530836311510合计300100.0管理统计学Managementstatistics\n数值型分组数据的众数1.众数的值与相邻两组频数的分布有关4.该公式假定众数组的频数在众数组内均匀分布2.相邻两组的频数相等时,众数组的组中值即为众数Mo3.相邻两组的频数不相等时,众数采用下列近似公式计算MoMo管理统计学Managementstatistics\n数值型分组数据的众数(算例)表3-5某车间50名工人日加工零件数分组表按零件数分组频数(人)累积频数105~110110~115115~120120~125125~130130~135135~140358141064381630404650合计50—【例】根据第三章表3-5中的数据,计算50名工人日加工零件数的众数管理统计学Managementstatistics\n中位数是从中间点将全部数据等分为两部分。与中位数类似的还有四分位数、八分位数、十分位数和百分位数等。它们分别是用3个点、7个点、9个点和99个点将数据四等分、八等分、十等分和100等分后各分位点上的值。这里只介绍四分位数的计算,其他分位数与之类似。分位数管理统计学Managementstatistics\n1.百分位数百分位数(percentile)是用99个点将排列好的数据100等分后各能给出从最小值到最大值区间内数据的信息分位点上的值。其中每个部分包含了1%的数据。百分位数的计算方法与中位数的类似分位数管理统计学Managementstatistics\n百分位数计算步骤:(1)将n个数据按一定的顺序(升序或降序)进行排列。(2)确定所求百分位数的位置。假设求第p百分位数,则该第p百分位数位置为:i=pn/100(3)确定百分位数。如果计算i的为整数,则直接在排列的数据列中找到第个变量即为所求。若i不为整数,则取位于两侧的变量的平均数作为所要求的百分位数。分位数管理统计学Managementstatistics\n2.四分位数一组数据排序后处于25%和75%位置上的值,称为四分位数(quartile),也称四分位点。四分位数是通过三个点将全部数据等分为四部分,其中每部分包含25%的数据。四分位数是指处在25%位置上的数值(下四分位数)和处在75%位置上的数值(上四分位数)。分位数管理统计学Managementstatistics\n设下四分位数为Q1,中间的四分位数为Q2,上四分位数为Q3。这三个四位数所在位置:Q1的位置为(n+1)/4Q2的位置为(n+1)/2,即中位数点的位置。Q3的位置为3(n+1)/4。Q1Q2Q325%25%25%25%分位数管理统计学Managementstatistics\n分位数\n定序数据的四分位数【例】根据第三章表3-2中的数据,计算甲城市家庭对住房满意状况评价的四分位数解:下四分位数(QL)的位置为:QL位置=(300)/4=75上四分位数(QL)的位置为:QU位置=(3×300)/4=225从累计频数看,QL在“不满意”这一组别中;QU在“一般”这一组别中。因此QL=不满意QU=一般表3-2甲城市家庭对住房状况评价的频数分布回答类别甲城市户数(户)累计频数非常不满意不满意一般满意非常满意2410893453024132225270300合计300—管理统计学Managementstatistics\n数值型未分组数据的四分位数(7个数据的算例)原始数据:23213032282526排序:21232526283032位置:1234567N+1QL=237+1QL位置=4=4=2QU位置=3(N+1)43(7+1)4==6QU=30管理统计学Managementstatistics\n数值型未分组数据的四分位数(6个数据的算例)原始数据:232130282526排序:212325262830位置:123456QL=21+0.75(23-21)=22.5QL位置=N+14=6+14=1.75QU位置=3(N+1)43(6+1)4==5.25QU=28+0.25(30-28)=28.5管理统计学Managementstatistics\n数值型分组数据的四分位数(计算公式)上四分位数:下四分位数:管理统计学Managementstatistics\n数值型分组数据的四分位数QL位置=50/4=12.5QU位置=3×50/4=37.5表3-5某车间50名工人日加工零件数分组表按零件数分组频数(人)累积频数105~110110~115115~120120~125125~130130~135135~140358141064381630404650合计50—【例4.6】根据第三章表3-5中的数据,计算50名工人日加工零件数的四分位数管理统计学Managementstatistics\n三、众数、中位数与均值的比较(一)正态分布时三者的关系正态分布是以算术平均数为对称轴,两边频数相等。其中频数最大的标志值就是数列居中位置的标志值,也就是权数最大、最具有代表性的那个变量值。因此,正态分布时,算术平均数、中位数和众数三者相等,即管理统计学Managementstatistics\n三、众数、中位数与均值的比较\n(二)偏态分布时三者的关系频数分布呈偏态时,算术平均数、中位数和众数的计算结果不同。当右偏时,算术平均数大于中位数,而中位数又大于众数,左偏时众数大于中位数,中位数大于算术平均数。在偏态分布情况下,算术平均数、中位数和众数的上述关系是容易理解的,由于算术平均数受极端值影响,在发生右偏出现较大极端值时,算术平均数将增加得更快,而中位数总是居于中间位置,。左偏同样可作类似的解释,从而有三、众数、中位数与均值的比较管理统计学Managementstatistics\n4.2数据分布的离散趋势测度变量的变异程度的度量则是将变量值的差异揭示出来,反映总体各变量值对其平均数这个中心的离中趋势。变异指标与平均指标分别从不同的侧面反映总体的数量特征。管理统计学Managementstatistics\n离散趋势测度极差四分位距平均差方差与标准差标准分数离散系数4.2数据分布的离散趋势测度管理统计学Managementstatistics\n极差(range)又称为全距,常用R表示,它是一组数据的最大值与最小值之差,即:极差表明数列中各变量值变动的范围。R越大,表明数列中变量值变动的范围越大,即数列中各变量值差异大;反之,R越小,表明数列中变量值的变动范围越小,即数列中各变量值差异越小。极差管理统计学Managementstatistics\n四分位距(quartiledeviation)是度量变异数的另一种方法,也称为内距或四分位差,是第一四分位数(下四分位数Q1)与第三四分位数(上四分位数Q3)的差,也就是75%百分位数与25%百分位数间的距离。它代表分布中间50%的距离。常用表示IQR,其计算公式为:四分位距管理统计学Managementstatistics\n四分位差【例】根据第三章表3-2中的数据,计算甲城市家庭对住房满意状况评价的四分位差解:设非常不满意为1,不满意为2,一般为3,满意为4,非常满意为5已知QL=不满意=2,QU=一般=3四分位差:QD=QU=QL=3–2=1表3-2甲城市家庭对住房状况评价的频数分布回答类别甲城市户数(户)累计频数非常不满意不满意一般满意非常满意2410893453024132225270300合计300—管理统计学Managementstatistics\n平均差(meandeviation)变量数列中各个变量值与算术平均数的绝对离差的平均数,常用MD表示。各变量值与平均数的离差的绝对值越大,平均差也越大,则说明变量值变动大,数列离散趋势越大;反之亦然。根据所给资料的形式不同,对平均差的计算可以划分为简单和加权式平均差两种形式。平均差管理统计学Managementstatistics\n(一)简单平均差对未经分组的数据资料,采用简单平均差,公式如下:平均差管理统计学Managementstatistics\n(二)加权式根据分组整理的数据计算平均差,应采用加权式,公式如下:平均差管理统计学Managementstatistics\n四、方差与标准差方差(variance)方差是变量数列中各变量值与其算术平均数差的平方。标准差(standarddeviation)标准差是方差的平方根,故又称均方差或均方差根,其计量单位与平均数的计量单位相同。根据给定资料的不同,对方差和标准差的求解也可以分为两种形式。管理统计学Managementstatistics\n对未经分组的数据资料,采用简单式,公式如下:方差的计算公式:标准差的计算公式:简单式管理统计学Managementstatistics\n根据分组整理的数据计算标准差,应采用加权式,公式如下:方差:标准差:加权式管理统计学Managementstatistics\n五、相对位置和相对离散程度的度量(一)标准分数标准分数(standardscore)也称标准化值或分数,它是变量值与其平均数的离差除以标准差后的值,是对每个数据在该组数据中相对位置的测量。常用字母z表示,有z分数是将原始数据进行了线性变换,它并没有改变一个数据在该数据组中的位置,也没有改变该组数据的分布形状,而只是将该组数据变为均值为0,标准差为1。管理统计学Managementstatistics\n离散系数(coefficientofvariation)通常是就标准差来计算的,因此,也称为标准差系数,它反映数列离散趋势的相对程度,是一组数据的标准差与其对应的平均数之比,是测度数据离散程度的相对指标,其计算公式如下:离散系数的作用主要用于比较不同总体或样本数据的离散程度。离散系数大的说明数据的离散程度也就大,离散系数小的说明数据的离散程度也就小。离散系数管理统计学Managementstatistics\n4.3数据分布的形状测度形状测度分布偏态测度分布峰态测度管理统计学Managementstatistics\n偏态(skewness)是对分布偏斜方向和程度的测度,是次数分配的非对称程度。它与平均数和标准差一样,是反映次数分布特征的又一重要指标。偏态通常分为两种:右偏(或正偏)与左偏(或负偏)。它们是与对称分布为标准相比较而言的。分布偏态测度管理统计学Managementstatistics\n统计分析中测定偏态系数的方法很多,一般采用动差概念计算,其计算公式为三阶中心动差与标准差的三次方之比。具体公式如下:分布偏态测度管理统计学Managementstatistics\n偏态1.数据分布偏斜程度的测度2.偏态系数=0为对称分布3.偏态系数>0为右偏分布4.偏态系数<0为左偏分布5.计算公式为:管理统计学Managementstatistics\n从上式可以看到,它是离差三次方的平均数再除以标准差的三次方。当分布对称时,离差三次方后正负离差可以相互抵消,因而的分子等于0,则=0;当分布不对称时,正负离差不能抵消,就形成了正与负的偏态系数。当为正值时,表示正偏离差值较大,可以判断为正偏或右偏;反之,为负值时,表示负偏离差值较大,可以判断为负偏或左偏。偏态系数的数值一般在0与±3之间,越接近0,分布的偏斜度越小;越接近±3,分布的偏斜度越大。分布偏态测度管理统计学Managementstatistics\n偏态:(实例)【例】已知1997年我国农村居民家庭按纯收入分组的有关数据如表4.9。试计算偏态系数表4-101997年农村居民家庭纯收入数据按纯收入分组(元)户数比重(%)500以下500~10001000~15001500~20002000~25002500~30003000~35003500~40004000~45004500~50005000以上2.2812.4520.3519.5214.9310.356.564.132.681.814.94管理统计学Managementstatistics\n户数比重(%)252015105农村居民家庭村收入数据的直方图偏态与峰度按纯收入分组(元)1000500←15002000250030003500400045005000→结论:1.为右偏分布2.峰度适中管理统计学Managementstatistics\n偏态系数:(计算过程)表4-10农村居民家庭纯收入数据偏态及峰度计算表按纯收入分组(百元)组中值Xi户数比重(%)Fi(Xi-X)Fi3(Xi-X)Fi45以下5—1010—1515—2020—2525—3030—3535—4040—4545—5050以上2.57.512.517.522.527.532.537.542.547.552.52.2812.4520.3519.5214.9310.356.564.132.681.814.94-154.64-336.46-144.87-11.840.1823.1689.02171.43250.72320.741481.812927.154686.511293.5346.520.20140.60985.492755.005282.948361.9846041.33合计—1001689.2572521.25管理统计学Managementstatistics\n偏态系数:(计算结果)根据上表数据计算得将计算结果代入公式得结论:偏态系数为正值,而且数值较大,说明农村居民家庭纯收入的分布为右偏分布,即收入较少的家庭占据多数,而收入较高的家庭则占少数,而且偏斜的程度较大管理统计学Managementstatistics\n峰度(kurtosis)是分布集中趋势高峰的形状,指次数分配曲线顶端的尖峭程度。在变量数列的分布特征中,常常将数分配曲线与正态曲线相比较,判断是尖顶还是平顶及其尖顶或平顶的程度。峰度通常分为三种:正态峰度、尖顶峰度与平顶峰度。当分配数列的次数比较集中于众数的位置,使次数分配曲线较正态分配曲线更为隆起的,属于尖顶峰度。当分配数列的次数,对众数来说比较分散,使次数分配曲线较正态分配曲线更为平滑的,属于平顶峰度。分布峰态测度管理统计学Managementstatistics\n测度峰度的方法一般运用统计动差法,即运用四阶中心动差与标准差的四次方对比,以此来判断各分布曲线峰度的尖平程度。公式如下:分布峰态测度管理统计学Managementstatistics\n峰度系数是统计中描述次数分布状态的又一个重要特征值,用以测定邻近数值周围变量值分布的集中或分散程度。它以四阶中心动差为测量标准,除以好是为了消除单位量纲的影响,而得到以无名数表示的相对数形式,以便在不同的分布曲线之间进行比较。由于正态分布的峰度系数为3,当>3时为尖峰分布,当<3时为平顶分布。分布峰态测度管理统计学Managementstatistics\n正态分布分布峰态测度管理统计学Managementstatistics\n偏态与峰态分布的形状扁平分布尖峰分布偏态峰态左偏分布右偏分布与标准正态分布比较!管理统计学Managementstatistics\n峰度系数系数:(实例计算结果)代入公式得【例4.18】根据表4-10中的计算结果,计算农村居民家庭纯收入分布的峰度系数结论:由于=3.4>3,说明我国农村居民家庭纯收入的分布为尖峰分布,说明低收入家庭占有较大的比重管理统计学Managementstatistics\n4.4用Excel计算描述统计量在本章的前三个小节中,我们介绍了描述数据集中趋势、离中趋势以及数据分布的常用统计量。但若都用人工手动计算,无疑操作性不强,比较费时且计算的准确率不高。在科技高速发展的今天,计算机成为我们生活中的有力助手。本节将展示如何利用Excel来计算这些统计量。管理统计学Managementstatistics\n4.4用Excel计算描述统计量在Excel中配备了许多统计函数,为了方便说明,我们以某班50名学生的年龄数据作为示例来进行说明如何应用excel来描述数据的集中趋势、离中趋势及数据的分布状况。管理统计学Managementstatistics\n4.4用Excel计算描述统计量将这些数据输入到Excel表的A1至A50中,然后进行以下操作:在菜单栏中选择“工具”下拉菜单,并选择“数据分析”选项。管理统计学Managementstatistics\n在“数据分析”对话框中选择分析工具“描述统计”4.4用Excel计算描述统计量管理统计学Managementstatistics\n4.4用Excel计算描述统计量点击确定按钮后,出现对话框在“输入区域”方框内框选取刚才输入的数据区域或者键入A1:A50;选择“汇总统计”单选框(表明需要输出全部的描述统计量);\n点击“确定”按钮,即得所需结果,如下所示4.4用Excel计算描述统计量\n在本章介绍的有些统计量如:调和平均数、几何平均数、四分位数、极差等在本表中没有出现,但可以运用Excel的函数工具进行计算,或通过在Excel中编写公式来实现。4.4用Excel计算描述统计量\n本章小节1.集中趋势各测度值的含义、计算方法、特点和应用场合2.离散程度各测度值的含义、计算方法、特点和应用场合偏态及峰度的测度方法用Excel计算描述统计量管理统计学Managementstatistics\nTheEnd管理统计学Managementstatistics查看更多