- 2022-08-24 发布 |
- 37.5 KB |
- 12页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
统计学期末复习试卷
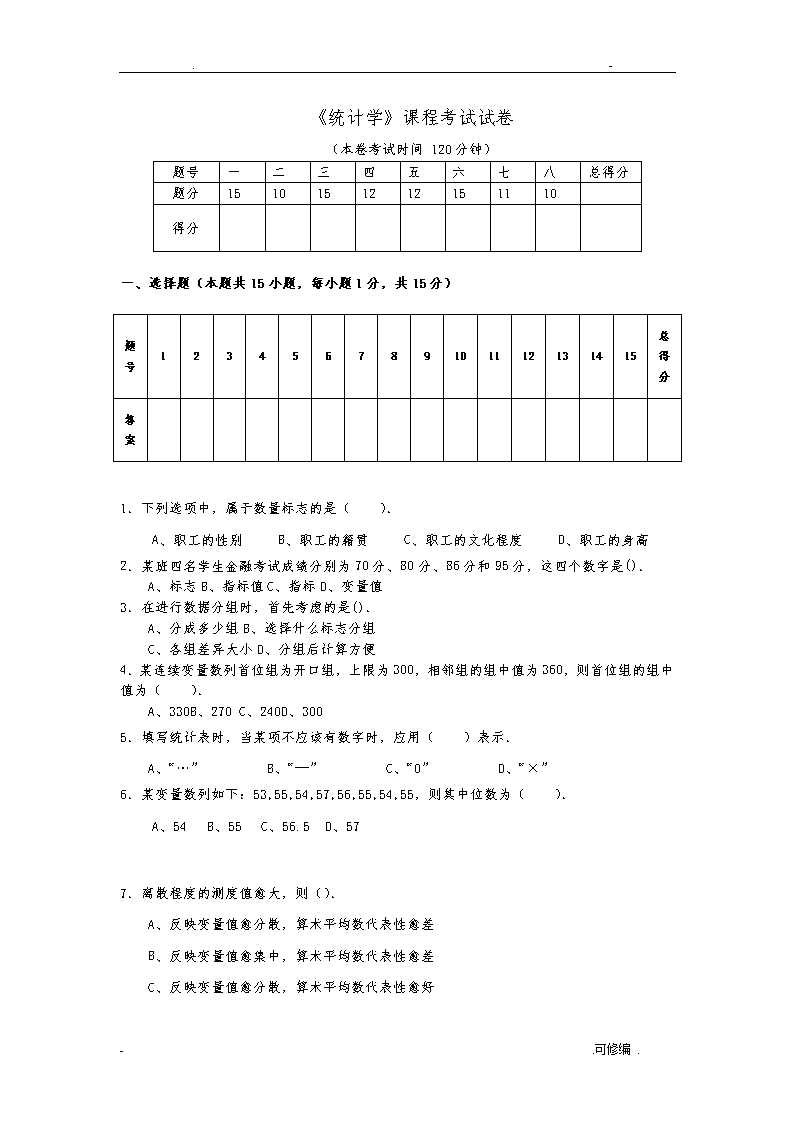
.-《统计学》课程考试试卷(本卷考试时间120分钟)题号一二三四五六七八总得分题分1510151212151110得分一、选择题(本题共15小题,每小题1分,共15分)题号123456789101112131415总得分答案1.下列选项中,属于数量标志的是().A、职工的性别B、职工的籍贯C、职工的文化程度D、职工的身高2.某班四名学生金融考试成绩分别为70分、80分、86分和95分,这四个数字是().A、标志B、指标值C、指标D、变量值3.在进行数据分组时,首先考虑的是().A、分成多少组B、选择什么标志分组C、各组差异大小D、分组后计算方便4.某连续变量数列首位组为开口组,上限为300,相邻组的组中值为360,则首位组的组中值为().A、330B、270C、240D、3005.填写统计表时,当某项不应该有数字时,应用()表示.A、“…”B、“—”C、“0”D、“×”6.某变量数列如下:53,55,54,57,56,55,54,55,则其中位数为(). A、54 B、55 C、56.5 D、577.离散程度的测度值愈大,则().A、反映变量值愈分散,算术平均数代表性愈差B、反映变量值愈集中,算术平均数代表性愈差C、反映变量值愈分散,算术平均数代表性愈好-.可修编.\n.-D、反映变量值愈集中,算术平均数代表性愈好8.矩估计的基本原理是().A、用样本矩估计总体矩B、使得似然函数达到最大C、使得似然函数达到最小D、小概率事件在一次试验中是不可能发生的9.在简单随机重复抽样条件下,当抽样容许误差缩小为原来的1/2时,则样本容量是原来的().A、2倍B、1/2倍C、4倍D、1/4倍10.在假设检验中,不能拒绝原假设意味着().A、原假设肯定是正确的B、原假设肯定是错误的C、没有证据证明原假设是正确的D、没有证据证明原假设是错误的11.线性相关的条件下,自变量的标准差为10,因变量的标准差为16,相关系数为0.9,则回归系数为().A、1.44B、0.56C、0.16D、14.412.最小平方法是要求().A、B、C、D、13.相关系数表明两个变量().A、是严格的函数关系B、不存在相关关系C、存在非线性相关关系D、不存在线性相关关系14.如果采用三项移动平均修匀时间数列,那么所得修匀数列比原数列首尾各少().A、一项数值B、二项数值C、三项数值D、四项数值15.实际工资=名义工资÷().A、上证指数B、居民消费价格指数C、商品零售价格指数D、纳斯达克指数二、多选题(本题共5小题,每小题2分,漏选错选得0分,共10分)题号12345总得分-.可修编.\n.-答案1.下列各项中,()是相对数.A、商品销售额B、人口密度C、学生出勤率D、人均产量E、平均工资2.在抽样推断中,样本容量的多少取决于().A、总体标准差的大小B、容许误差的大小C、抽样推断的置信水平的大小D、抽样的方式E、抽样的方法3.某一批原材料的质量实际上是不符合生产标准,检验部门抽取1%的原材料检验,得出结论是该批原材料的质量符合生产标准,说明().A、检验部门犯了第一类错误B、检验部门犯了第二类错误C、犯这种错误的概率是D、犯这种错误的概率是E、犯这种错误的原因是检验部门没有遵循随机原则4.如果两个变量之间的线性相关程度很高,则其相关系数应接近于().A、0.5B、-0.5C、0D、1E、-15.时间数列的构成要素有().A、按标志进行的统计分组B、频率C、现象所属时间D、统计指标值E、频数三、描述性统计计算题(本题共15分)某商店职工奖金资料如下:按奖金分组(元/人)x各组工资奖金总额m(元)f50100-.可修编.\n.-609607014008072090270合计3450填充上面的表格,并根据上述资料计算平均奖金、标准差及标准差系数。四、统计推断模块的计算题(本大题共12分)教育局要对某高校的基础教育质量进行调研,现对该校大二学生期末数学考试进行抽样调查,抽取16为同学的期末数学考试成绩为:80,77,65,88,81,68,72,91,58,75,79,80,67,89,73,66假设该校大二学生期末数学分数服从正态分布,请解答如下问题:(1)用点估计方法估计该校大二学生的平均数学成绩和数学成绩的标准差;(3分)(2)求该校大二学生的平均数学成绩的95%的置信区间。(7分)(3)说明(2)中求得置信区间的含义.(2分)-.可修编.\n.-五、统计推断模块的计算题(本大题共12分)万里橡胶制品厂生产的汽车轮胎平均寿命为40,000公里,标准差为7500公里。该厂经过技术革新试制了一种新轮胎比原轮胎平均寿命明显延长,则可大批量生产。技术人员抽取了100只新轮胎,测得平均寿命为41,000公里,汽车轮胎的平均寿命服从正态分布。请解答如下问题:(1)试利用样本观察的结果,说明该厂是否应大批量生产这种新轮胎。(α=0.05)(+9分)(2)简述假设检验中两类错误,本题检验结果可能犯哪类错误,犯错误的概率是多少?(+3分)-.可修编.\n.-六、统计建模分析模块的计算题(本大题共15分)某地1996~2001年的年末人口数如下表:单位:万人年份年末人口数ytt2ty199619971998199920002001222430364454123456合计21021以1996年对应t=1,1997年对应t=2,…,运用最小二乘法建立t与年末人口数y的一元线性回归方程,并预测2002年末和2004年末的人口总数。七、统计建模分析模块的计算题(本题共11分)某商店按季统计的3年12个季度冰箱的销售额资料,如下表,(计算保留2为小数)-.可修编.\n.-——季度销售额Yt1234年份200926537333326620102513793743092011272437396348季节平均数季节指数(%)试回答以下问题(计算保留2为小数):(1)完成上表(不考虑长期趋势)(8分)(2)若已知2012年第1季度销售额为420万元,预测2012第2季度的销售额。(3分)八、统计建模分析模块的计算题(本题共10分)-.可修编.\n.-某商场四种电器的销售情况如下:电器名称6月份价格7月份价格6月份销售量7月份销售量电视机12001200800820电冰箱180016007001200洗衣机15001700500400空调机250021004001000试计算该商场的(1)拉氏价格指数;(+5分)(2)派氏销售量指数。(+5分)附表1:z分布临界值表-.可修编.\n.-α0.4000.3000.2000.1000.0500.0250.0200.0100.0050.001zα0.2530.5240.8421.2821.6451.9602.0542.3262.5763.090zα/20.8421.0361.2821.6451.9602.2402.3262.5762.8073.291附表2:t分布临界值表(上α分位点)单侧α0.10.050.0250.010.005双侧α0.20.10.050.020.0113.0776846.31375212.706231.8205263.6567421.8856182.9199864.3026536.9645579.92484331.6377442.3533633.1824464.5407035.84090941.5332062.1318472.7764453.7469474.60409551.4758842.0150482.5705823.364934.03214361.4397561.943182.4469123.1426683.70742871.4149241.8945792.3646242.9979523.49948381.3968151.8595482.3060042.8964593.35538791.3830291.8331132.2621572.8214383.249836101.3721841.8124612.2281392.7637693.169273111.363431.7958852.2009852.7180793.105807121.3562171.7822882.1788132.6809983.05454131.3501711.7709332.1603692.6503093.012276141.345031.761312.1447872.6244942.976843-.可修编.\n.-151.3406061.753052.131452.602482.946713161.3367571.7458842.1199052.5834872.920782171.3333791.7396072.1098162.5669342.898231181.3303911.7340642.1009222.552382.87844191.3277281.7291332.0930242.5394832.860935201.3253411.7247182.0859632.5279772.84534附表3:F分布临界值表(α=0.05)-.可修编.\n.--.可修编.\n.--.可修编.查看更多