生物统计学课件00008

生物统计学课件00008

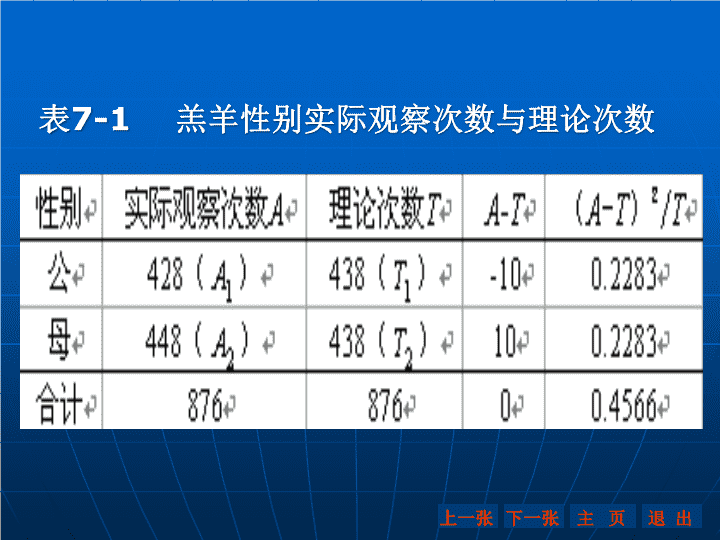
第7章次数资料分析——2检验本章将分别介绍对次数资料、等级资料进行统计分析的方法。下一张主页退出上一张\n第一节2统计量与2分布一、2统计量的意义为了便于理解，现结合一实例说明2(读作卡方)统计量的意义。根据遗传学理论，动物的性别比例是1:1。统计某羊场一年所产的876只羔羊中，有公羔428只，母羔448只。按1:1的性别比例计算，公、母羔均应为438只。以A表示实际观察次数，T表示理论次数，可将上述情况列成表7-1。下一张主页退出上一张\n表7-1羔羊性别实际观察次数与理论次数下一张主页退出上一张\n从表7-1看到，实际观察次数与理论次数存在一定的差异，这里公、母各相差10只。这个差异是属于抽样误差(把对该羊场一年所生羔羊的性别统计当作是一次抽样调查)、还是羔羊性别比例发生了实质性的变化?要回答这个问题，首先需要确定一个统计量用以表示实际观察次数与理论次数偏离的程度；然后判断这一偏离程度是否属于抽样误差，即进行显著性检验。\n为了度量实际观察次数与理论次数偏离的程度，最简单的办法是求出实际观察次数与理论次数的差数。从表7-1看出：A1-T1=-10，A2-T2=10，由于这两个差数之和为0，显然不能用这两个差数之和来表示实际观察次数与理论次数的偏离程度。为了避免正、负抵消，可将两个差数A1-T1、A2-T2平方后再相加，即计算∑(A-T)2，其值越大，实际观察次数与理论次数相差亦越大，反之则越小。但利用∑(A-T)2表示实际观察次数与理论次数的偏离程度尚有不足。例如某一组实际观察次数为下一张主页退出上一张\n505、理论次数为500，相差5；而另一组实际观察次数为26、理论次数为21，相差亦为5。显然这两组实际观察次数与理论次数的偏离程度是不同的。因为前者是相对于理论次数500相差5，后者是相对于理论次数21相差5。为了弥补这一不足，可先将各差数平方除以相应的理论次数后再相加，并记之为2，即下一张主页退出上一张\n(7-1)也就是说2是度量实际观察次数与理论次数偏离程度的一个统计量，2越小，表明实际观察次数与理论次数越接近；2=0，表示两者完全吻合；2越大，表示两者相差越大。对于表7-1的资料，可计算得表明实际观察次数与理论次数是比较接近的。下一张主页退出上一张\n二、2分布上面在属于离散型随机变量的次数资料的基础上引入了统计量2，它近似地服从统计学中一种连续型随机变量的概率分布2分布。下面对统计学中的2分布作一简略介绍。设有一平均数为μ、方差为的正态总体。现从此总体中独立随机抽取n个随机变量：x1、x2、…、xn，并求出其标准正态离差：，，…，下一张主页退出上一张\n记这n个相互独立的标准正态离差的平方和为2：(7-2)它服从自由度为n的2分布，记为～2(n)；下一张主页退出上一张\n若用样本平均数代替总体平均数μ，则随机变量(7-3)服从自由度为n-1的2分布，记为～下一张主页退出上一张\n显然，2≥0，即2的取值范围是[0,+∞；2分布密度曲线是随自由度不同而改变的一组曲线。随自由度的增大，曲线由偏斜渐趋于对称；df≥30时，接近平均数为的正态分布。图7-1给出了几个不同自由度的2概率分布密度曲线。下一张主页退出上一张\n三、的连续性矫正由(7-1)式计算的2只是近似地服从连续型随机变量2分布。在对次数资料进行2检验利用连续型随机变量2分布计算概率时，常常偏低，特别是当自由度为1时偏差较大。Yates(1934)提出了一个矫正公式，矫正后的2值记为：=(7-4)下一张主页退出上一张\n当自由度大于1时，(7-1)式的2分布与连续型随机变量2分布相近似，这时，可不作连续性矫正，但要求各组内的理论次数不小于5。若某组的理论次数小于5，则应把它与其相邻的一组或几组合并，直到理论次数大于5为止。下一张主页退出上一张\n第二节适合性检验一、适合性检验的意义判断实际观察的属性类别分配是否符合已知属性类别分配理论或学说的假设检验称为适合性检验。下一张主页退出上一张\n在适合性检验中，无效假设为H0：实际观察的属性类别分配符合已知属性类别分配的理论或学说；备择假设为HA：实际观察的属性类别分配不符合已知属性类别分配的理论或学说。并在无效假设成立的条件下，按已知属性类别分配的理论或学说计算各属性类别的理论次数。因所计算得的各个属性类别理论次数的总和应等于各个属性类别实际观察次数的总和，即独立的理论次数的个数等于属性类别分下一张主页退出上一张\n类数减1。也就是说，适合性检验的自由度等于属性类别分类数减1。若属性类别分类数为k，则适合性检验的自由度为k-1。然后根据(7-1)或(7-4)式计算出2或2c。将所计算得的2或2c值与根据自由度k-1查2值表(附表8)所得的临界2值：20.05、20.01比较：下一张主页退出上一张\n若2(或2c)＜20.05，P＞0.05，表明实际观察次数与理论次数差异不显著，可以认为实际观察的属性类别分配符合已知属性类别分配的理论或学说；若20.05≤2(或2c)＜20.01，0.01＜P≤0.05，表明实际观察次数与理论次数差异显著，实际观察的属性类别分配显著不符合已知属性类别分配的理论或学说；若2(或2c)≥20.01，P≤0.01，表明实际观察次数与理论次数差异极显著，实际观察的属性类别分配极显著不符合已知属性类别分配的理论或学说。\n二、适合性检验的方法下面结合实例说明适合性检验方法。【例7.1】在进行山羊群体遗传检测时，观察了260只白色羊与黑色羊杂交的子二代毛色，其中181只为白色，79只为黑色，问此毛色的比率是否符合孟德尔遗传分离定律的3∶1比例?下一张主页退出上一张\n检验步骤如下：（一）提出无效假设与备择假设H0：子二代分离现象符合3∶1的理论比例。HA：子二代分离现象不符合3∶1的理论比例。（二）选择计算公式由于本例是涉及到两组毛色（白色与黑色），属性类别分类数k=2，自由度df=k-1=2-1=1，须使用（7—4）式来计算。下一张主页退出上一张\n（三）计算理论次数根据理论比率3∶1求理论次数：白色理论次数：T1=260×3/4=195黑色理论次数：T2=260×1/4=65或T2=260-T1=260-195=65（四）计算\n表7—22c计算表下一张主页退出上一张\n(五)查临界2值，作出统计推断当自由度df=1时，查得20.05（1）=3.84，计算的2c<20.05（1），P>0.05，不能否定H0，表明实际观察次数与理论次数差异不显著，可以认为白色羊与黑色羊的比率符合孟德尔遗传分离定律3∶1的理论比例。\n【例7.2】在研究牛的毛色和角的有无两对相对性状分离现象时，用黑色无角牛和红色有角牛杂交，子二代出现黑色无角牛192头，黑色有角牛78头，红色无角牛72头，红色有角牛18头，共360头。试问这两对性状是否符合孟德尔遗传规律中9∶3∶3∶1的遗传比例？下一张主页退出上一张\n检验步骤：（一）提出无效假设与备择假设H0：实际观察次数之比符合9∶3∶3∶1的理论比例。HA：实际观察次数之比不符合9∶3∶3∶1的理论比例。（二）选择计算公式由于本例的属性类别分类数k=4：自由度df=k-1=4-1=3>1，故利用（7—1）式计算2。（三）计算理论次数依据各理论比例9:3:3:1计算理论次数：\n黑色无角牛的理论次数T1：360×9/16=202.5；黑色有角牛的理论次数T2：360×3/16=67.5；红色无角牛的理论次数T3：360×3/16=67.5；红色有角牛的理论次数T4：360×1/16=22.5。或T4=360-202.5-67.5-67.5=22.5（四）列表计算2下一张主页退出上一张\n表7—32计算表\n=0.5444+1.6333+1.6333+0.9=4.711（五）查临界2值，作出统计推断当df=3时，20.05(3)=7.81，因2<2005(3)，P>0.05，不能否定H0，表明实际观察次数与理论次数差异不显著，可以认为毛色与角的有无两对性状杂交二代的分离现象符合孟德尔遗传规律中9∶3∶3∶1的遗传比例。下一张主页退出上一张\n第三节独立性检验一、独立性检验的意义对次数资料，除进行适合性检验外，有时需要分析两类因子是相互独立还是彼此相关。如研究两类药物对家畜某种疾病治疗效果的好坏，先将病畜分为两组，一组用第一种药物治疗，另一组用第二种药物治疗，然后统计每种药物的治愈头数和未治愈头数。\n这时需要分析药物种类与疗效是否相关，若两者彼此相关，表明疗效因药物不同而异，即两种药物疗效不相同；若两者相互独立，表明两种药物疗效相同。这种根据次数资料判断两类因子彼此相关或相互独立的假设检验就是独立性检验。独立性检验实际上是基于次数资料对子因子间相关性的研究。下一张主页退出上一张\n独立性检验与适合性检验是两种不同的检验方法，除了研究目的不同外，还有以下区别：（一）独立性检验的次数资料是按两因子属性类别进行归组。根据两因子属性类别数的不同而构成2×2、2×c、r×c列联表（r为行因子的属性类别数，c为列因子的属性类别数）。而适合性检验只按某一因子的属性类别将如性别、表现型等次数资料归组。\n（二）适合性检验按已知的属性分类理论或学说计算理论次数。独立性检验在计算理论次数时没有现成的理论或学说可资利用，理论次数是在两因子相互独立的假设下进行计算。（三）在适合性检验中确定自由度时，只有一个约束条件：各理论次数之和等于各实际次数之和，自由度为属性类别数减1。而在r×c列联表的独立性检验中，共有rc个理论次数，但受到以下条件的约束：下一张主页退出上一张\n1、rc个理论次数的总和等于rc个实际次数的总和；2、r个横行中的每一个横行理论次数总和等于该行实际次数的总和。但由于r个横行实际次数之和的总和应等于rc个实际次数之和，因而独立的行约束条件只有r-1个；3、类似地，独立的列约束条件有c-1个。因而在进行独立性检验时，自由度为rc-1-(r-1)-(c-1)=(r-1)(c-1)，即等于（横行属性类别数-1）×（直列属性类别数-1）。\n二、独立性检验的方法（一）2×2列联表的独立性检验2×2列联表的一般形式如表7—10所示，其自由度df=(c-1)(r-1)=(2-1)(2-1)=1，在进行2检验时，需作连续性矫正，应计算值。下一张主页退出上一张\n表7—102×2列联表的一般形式下一张主页退出上一张其中Aij为实际观察次数，Tij为理论次数。\n【例7.7】某猪场用80头猪检验某种疫苗是否有预防效果。结果是注射疫苗的44头中有12头发病，32头未发病；未注射的36头中有22头发病，14头未发病，问该疫苗是否有预防效果？1、先将资料整理成列联表\n表7—112×2列联表下一张主页退出上一张\n2、提出无效假设与备择假设H0：发病与否和注射疫苗无关，即二因子相互独立。HA：发病与否和注射疫苗有关，即二因子彼此相关。3、计算理论次数根据二因子相互独立的假设，由样本数据计算出各个理论次数。二因子相互独立，就是说注射疫苗与否不影响发病率。也就是说注射组与未注射组的理论发病率应当相同，均应等于总发病率34/80=0.425=42.5%。依此计算出各个理论次数如下：\n注射组的理论发病数：T11=44×34/80=18.7注射组的理论未发病数：T12=44×46/80=25.3，或T12=44-18.7=25.3；\n未注射组的理论发病数：T21=36×34/80=15.3，或T21=34-18.7=15.3；未注射组的理论未发病数：T22=36×46/80=20.7，或T22=36-15.3=20.7。下一张主页退出上一张\n从上述各理论次数Tij的计算可以看到，理论次数的计算利用了行、列总和，总总和，4个理论次数仅有一个是独立的。表7-11括号内的数据为相应的理论次数。4、计算值将表7-11中的实际次数、理论次数代入(7—4)式得：\n\n5、由自由度df=1查临界2值，作出统计推断因为20.01（1）=6.63，而=7.944>20.01（1），P<0.01，否定H0，接受HA，表明发病率与是否注射疫苗极显著相关，这里表现为注射组发病率极显著低于未注射组，说明该疫苗是有预防效果的。在进行22列联表独立性检验时，还可利用下述简化公式（7-6）计算：下一张主页退出上一张\n（7—6）在（7-6）式中，不需要先计算理论次数，直接利用实际观察次数Aij，行、列总和Ti.、T.j和总总和T..进行计算，比利用公式（7-4）计算简便，且舍入误差小。对于【例7.7】，利用（7-6）式可得：\n所得结果与前面计算计算的相同。（二）2×c列联表的独立性检验2×c列联表是行因子的属性类别数为2，列因子的属性类别数为c（c3）的列联表。其自由度df=(2-1)(c-1)=(c-1)，因为c3，所以自由度大于2，在进行2检验时，不需作连续性矫正。2×c表的一般形式见表7—12。下一张主页退出上一张\n表7—122×c联列表一般形式下一张主页退出上一张\n其中（i=1，2；j=1，2，…，c）为实际观察次数。【例7.8】在甲、乙两地进行水牛体型调查，将体型按优、良、中、劣四个等级分类，其结果见表7—13，问两地水牛体型构成比是否相同。下一张主页退出上一张\n表7—13两地水牛体型分类统计下一张主页退出上一张\n这是一个2×4列联表独立性检验的问题。检验步骤如下：1.提出无效假设与备择假设H0：水牛体型构成比与地区无关，即两地水牛体型构成比相同。HA：水牛体型构成比与地区有关，即两地水牛体型构成比不同。\n2.计算各个理论次数，并填在各观察次数后的括号中计算方法与2×2表类似，即根据两地水牛体型构成比相同的假设计算。如优等组中，甲地、乙地的理论次数按理论比率20/135计算；良等组中,甲地、乙地的理论次数按理论比率15/135计算；中等、劣等组中,甲地、乙地的理论次数分别按理论比率80/135和20/135计算。下一张主页退出上一张\n甲地优等组理论次数：T11=90×20/135=13.3，乙地优等组理论次数：T21=45×20/135=6.7，或T21=20-13.3=6.7；其余各个理论次数的计算类似。3.计算计算2值\n\n4.由自由度df=3查临界2值，作出统计推断因为20..05（3）=7.81，而2=7.582<20..05（3），p>0.05，不能否定H0,可以认为甲、乙两地水牛体型构成比相同。在进行2×c列联表独立性检验时，还可利用下述简化公式（7-7）或（7-8）计算2：（7—7）下一张主页退出上一张\n或（7—8）（7-7）与（7-8）式的区别在于：（7-7）式利用第一行中的实际观察次数A1j和行总和T1.；（7-8）式利用第二行中的实际观察次数A2j和行总和T2.，计算结果相同。对于[例7.7]利用（7-8）式计算2值得：\n计算结果与利用（7—1）式计算的结果因舍入误差略有不同。此外，在畜牧、水产科学研究中，有时需将数量性状资料以等级分类，如剪毛量分为特等、一等、二等，产奶量分为高产与低产等，这些由数量性状资料转化为质量性状的次数资料检验，也可用2检验。【例7.9】分别统计了A、B两个品种各67头经产母猪的产仔情况，结果见表7—14，问A、B两品种的产仔构成比是否相同？下一张主页退出上一张\n表7—14A、B两个品种产仔数的分类统计\n1、提出无效假设与备择假设H0：A、B两个品种产仔数分级构成比相同。HA：A、B两个品种产仔数分级构成比不同。2、计算2值用简化公式（7—7）计算为：下一张主页退出上一张\n3、由自由度df=(2-1)(3-1)=2查临界2值，作出统计推断因为20.05（2）=9.21，2>20.01，P<0.01，所以否定H0，接受HA，表明A、B两品种产仔数构成比差异极显著。需要应用2检验的再分割法来具体确定分级构成比差异在那样的等级。\n表7—1521计算表下一张主页退出上一张4、2检验的再分割法（1）先对两个品种产仔数在9头以下和10—12头进行2检验，分割后的情况见表7—15。\n利用简化公式（7-7）计算21值为：由df1=2-1=1，查2值表得：20.05（1）=3.841，因为21<20.05（1），P>0.05，表明这两个品种的产仔数在9头以下和10—12头这两个级别内的比率差异不显著。（2）对产仔数在13头以上组与其他合并组（即9头以下和10—12头两个组的合并）进行2检验，分割后见表7—16。下一张主页退出上一张\n表7—1622计算表利用简化公式（7-7）计算22值为：\n由df2=2-1=1，查2值表得：20.05（1）=3.84，20.01（1）=6.63，因为22>20.01（1），P<0.01，表明这两个品种的产仔数在合并组与13头以上组的比率差异极显著。其中B品种产仔数在13头以上的比率为29/67=42.38%，极显著高于A品种产仔数在13头以上的比率6/67=8.96%。或者说B品种产仔数在合并组（12头以下）的比率为38/67=56.72%，极显著低于A品种产仔数在合并组（12头以下）的比率61/67=91.04%。下一张主页退出上一张\n经分割检验后df=df1+df2=1+1=22=23.25=21+22=2.93+20.458=23.3882略小于21+22，是由于计算中的舍入误差所致。下一张主页退出上一张\n（三）r×c列联表的独立性检验r×c表是指行因子的属性类别数为r（r>2），列因子的属性类别数为c(c>2)的列联表。其一般形式见表7-17。\n表7—17r×c列联表的一般形式\n其中Aij（i=1,2,…r;j=1,2,…c）为实际观察次数。r×c列联表各个理论次数的计算方法与上述（2×2）、（2×c）表适合性检验类似。但一般用简化公式计算2值，其公式为：（7—9）【例7.10】对三组奶牛（每组39头）分别喂给不同的饲料，各组发病次数统计如下表，问发病次数的构成比与所喂饲料是否有关？下一张主页退出上一张\n表7—18三组牛的发病次数资料\n检验步骤如下：1、提出无效假设与备择假设H0：发病次数的构成比与饲料种类无关，即二者相互独立。HA：发病次数的构成比与饲料种类有关，即二者彼此独立。2、计算理论次数对于理论次数小于5者，将相邻几个组加以合并（见表7—19），合并后的各组的理论次数均大于5。下一张主页退出上一张\n表7—19资料合并结果（注：括号内为理论次数）下一张主页退出上一张\n3、计算2值利用（7-9）式计算2值，得：\n4、查临界2值，进行统计推断由自由度df=(4-1)(3-1)=6，查临界2值得：20..05（6）=12.59因为计算所得的2<20.05（6），P>0.05，不能否定HO，可以认为奶牛的发病次数的构成比与饲料种类相互独立，即用三种不同的饲料饲喂奶牛，各组奶牛发病次数的构成比相同。下一张主页退出上一张