综合 社会统计学复习

综合 社会统计学复习

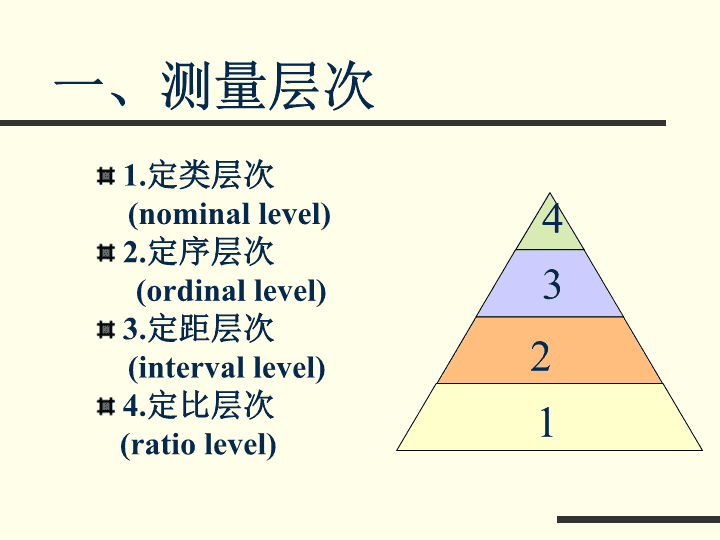
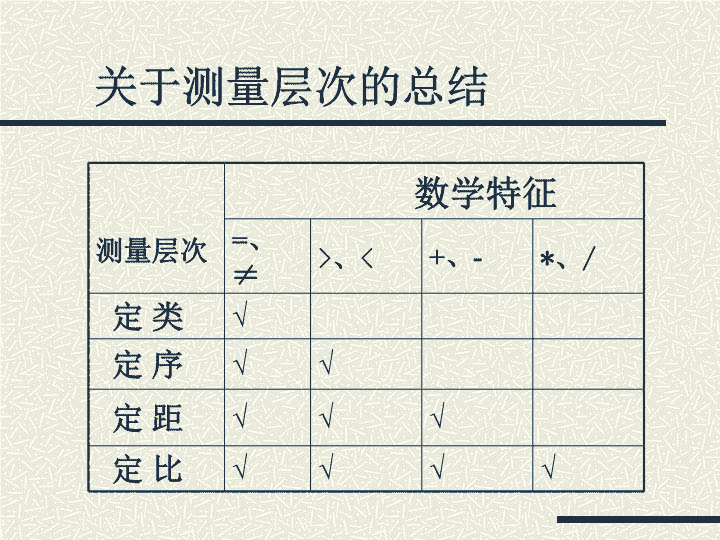
社会统计学复习1.变量层次：四个层次的特征2.单变量分布的简化3.双变量的相关4.抽样分布5.参数估计6.假设检验\n一、测量层次1.定类层次(nominallevel)2.定序层次(ordinallevel)3.定距层次(intervallevel)4.定比层次(ratiolevel)1243\n关于测量层次的总结测量层次数学特征=、≠>、<+、-*、/定类√定序√√定距√√√定比√√√√\n对测量尺度层次的判断较低层次的测量尺度较高层次的测量尺度低测量精度高少计算方法多小信息数量大\n二、简化一个变量的分布基本技术1.定类层次2.定序层次3.定距层次集中趋势测量离散趋势测量\n1.定类层次适用于简化一个定类变量资料的方法有次数分布、比例、比率、对比值和图示（长条图、圆瓣图）。\n2、定序层次次数、比例、比率、对比值、长条图和圆形图等，适用于简化定类资料，也可以用于简化定序资料。适用于定序层次而不可用于定类层次的，有累加次数和累加百分率。\n3、定距层次以上方法对定距层次的变量都适用，但定距层次的变量在使用这些方法时必须先进行分组，由具体数字转化为区间。定距变量还可以使用直方图、折线图等。\n集中趋势测量法所谓集中趋势测量法，就是找出一个数值来代表变量的资料分布，以反映资料的集中情况。集中趋势测量法有一个特殊意义，就是可以根据这个代表值来估计或预测每个研究对象(即个案)的数值。这样的估计或预测，由于所根据的数值最有代表性，故所发生错误的总和是最小的。\n所谓离散趋势测量法是指求出一个值来表示一个变量上的个案与个案之间的差异情况\n正态曲线的一般形式\n两个参数对曲线形状的影响当x和确定后，正态曲线的图形也就唯一被确定了。两者合称正态分布曲线的两个参数。\n标准分的意义它是以均值为基点，以标准差为度量单位，因此，各总体之间可以通过标准分进行合理的比较和相加。\n正态分布的计算设x-N，在对某一区间的概率(面积或个案出现的概率)计算时，首先要换算成正态分布：\n三、两个变量的相关指一个变量的值与另一个变量的值有连带性，即如果一个变量的值发生变化，另一个变量的值也有变化，则两个变量就是相关了。\n简化相关所谓相关测量法就是以一个统计值表示变量与变量之间的关系，这个值通常称为相关系数。\n相关系数的选择1.变量的测量层次2.变量的关系是对称的，还是不对称的(这一点不做严格要求)3.消减误差比例意义实际研究中更多考虑的是1、3\n变量层次相关系数对称性PRE值域定类-定类Lambda系数Tau-y对称不对称有有[0,1][0,1]定序-定序rs系数G系数dyx系数Tau系数对称对称不对称不对称无有有无[0,1][-1,1][-1,1]不定定距-定距rr2对称对称无有[-1,1][0,1]定类-定距E2不对称有[0,1]\n四、抽样分布抽样分布是根据概率分布的原则而成立的理论性分布，显示由同一总体中反复不断的抽取不同样本时，各个可能出现的样本统计量的分布情况。注意区分总体分布、样本分布、抽样分布。\n抽样分布正态分布总体的抽样分布服从正态分布。如果样本足够大，N>30，不管原分布如何，抽样分布接近正态分布抽样分布的均值就是总体的均值。抽样误差就是抽样分布中均值的标准差。那么，抽样分布的均值两旁，包括多少个样本均值呢？\n如图：\n五、参数估计点估计区间估计区间估计的公式区间估计与必要样本容量\n区间估计与假设检验的关系二者的区别二者的相同点二者的相互转化（利用置信区间进行假设检验）\n六、假设检验主要问题：1、假设检验的基本思想2、假设检验的步骤3、假设检验中的两类错误4、总结\n假设检验的基本思想假设检验的基本思想——基于小概率原理的反证法。两个特点：采用反证法依据的是小概率原理——小概率事件在一次观察中几乎不可能发生的原则。\n建立总体假设H0，H1抽样得到样本观察值12选择统计量确定H0为真时的抽样分布3根据具体决策要求确定α确定分布上的临界点C和检验规则计算检验统计量的数值比较并作出检验判断7456假设检验的步骤\n总体均值、比例和方差的假设检验1、总体方差已知时对正态总体均值或均值差的检验——Z检验法2、总体方差未知时对正态总体均值或均值差的检验——t检验法3、大样本总体均值或均值差的检验—Z检验法4、大样本总体比例或比例差的假设检验——采用Z检验法5、小样本总体方差的假设检验——采用卡方检验法\n一些常见的错误观念接受原假设=原假设正确接受原假设时，原假设正确的可能性（判断正确的概率）=1-“差异显著”=有很大差异对同一检验问题，两个假设互换位置，检验结论并没有什么不同。……\n典型的数据分析方法（部分）集中趋势离散趋势相关回归假设检验众数定类变量品质相关2检验异众比中位数等级相关四分位差Z、t检验定序变量均值相关回归标准差F、t检验定距变量\n归纳：定类-定类定类-定序X2检定定序-定序——Z、T检定定类-定距定序-定距F检定定距-定距\n描述统计与推断统计中相关回归分析的差别描述统计:不需要对随机误差项作出各种假定,各种参数估计值是具体数值,是对总体存在的相关关系的描述,不存在显著性检验.推断统计:需要对随机误差项作出各种假定,各种参数估计量是随机变量,抽取的样本不同时,得到的估计值也不同.可以用来推断总体.需要进行各种检验.\n相关分析与回归分析相关分析是用一个指标来表明现象间依存关系的密切程度。回归分析是用数学模型近似表达变量间的平均变化关系。相关分析可以不必确定变量中哪个是自变量，哪个是因变量，其所涉及的变量都是随机变量。\n相关分析与回归分析回归分析必须事先确定具有相关关系的变量中哪个为自变量，哪个为因变量。一般地说，回归分析中因变量是随机的，而把自变量作为研究时给定的非随机变量。一定要始终注意把定性分析和定量分析结合起来，在定性分析的基础上开展定量分析。\n样本回归函数与总体回归函数区别总体回归线是未知的，只有一条。样本回归线是根据样本数据拟合的，每抽取一组样本，便可以拟合一条样本回归线。总体回归函数中的和β是未知的参数，表现为常数。而样本回归函数中的是随机变量，其具体数值随所抽取的样本观测值不同而变动。\n样本回归函数与总体回归函数区别总体回归函数中的Et是Ｙ与未知的总体回归线之间的纵向距离，它是不可直接观测的。而样本回归函数中的ｅ是Ｙ与样本回归线之间的纵向距离，当根据样本观测值拟合出样本回归线之后，可以计算出ｅ的具体数值。\n练习：1．我们的研究假设是：不同类的专业卫生技术人员对当地的卫生事业的发展有不同的满意程度。为求证这一假设，我们从全部卫生技术人员中抽取一个随机样本[n=490]，下表就是两个变量的交互分类资料。①试写出虚无假设；②计算卡方值；③如果所选取的显著程度是0.05，则统计结果是支持还是否定研究假设？④试计算相关系数。\n专业卫生技术人员对卫生事业发展的态度态度卫生人员总数西医医士护士中医满意10854414207一般3133132299不满意1453108184总数2841185434490\n2．以下是婚姻美满与文化程度的随机抽样调查结果问：文化程度与婚姻美满状况是否相关？提出研究结论。[显著性水平为0.05]文化婚姻大学中学小学美满一般不美满916583018347\n3.以下是生活期望值与个人成就的抽样调查：生活期望值108764321个人成就791042132求（1）回归直线；（2）相关系数和判定系数并解释其意义；（3）是否具有推论意义[显著性水平0.05]