- 2022-08-24 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
体育统计学参考公式
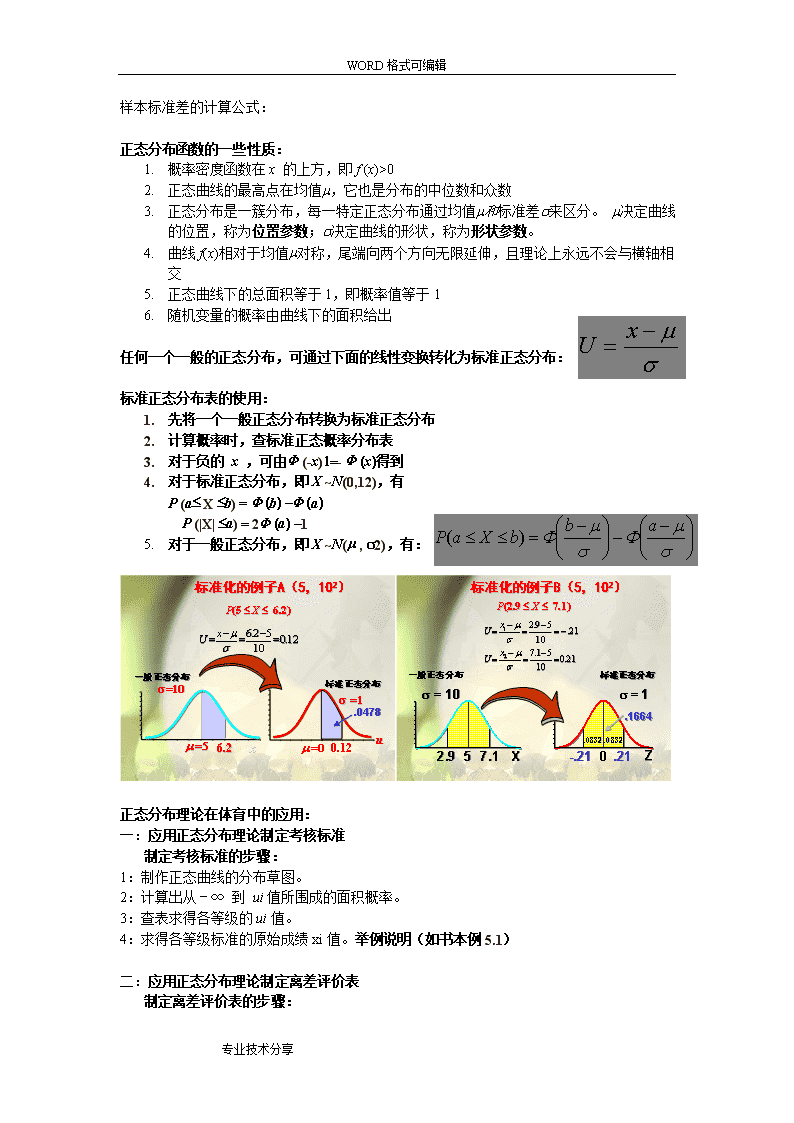
WORD格式可编辑体育统计学参考公式体育中常用的连加求和运算:为了避免符号过于复杂,今后凡在求和范围可以看清的条件下,通常将∑号上下标省略不写,简记为:中位数:几何平均数:算术平均数:全距(极差,两极差):R=最大值(Xmax)-最小值(Xmin)总体方差的计算公式:总体标准差的计算公式:样本方差的计算公式:专业技术分享\nWORD格式可编辑样本标准差的计算公式:正态分布函数的一些性质:1.概率密度函数在x的上方,即f(x)>02.正态曲线的最高点在均值m,它也是分布的中位数和众数3.正态分布是一簇分布,每一特定正态分布通过均值m和标准差s来区分。m决定曲线的位置,称为位置参数;s决定曲线的形状,称为形状参数。4.曲线f(x)相对于均值m对称,尾端向两个方向无限延伸,且理论上永远不会与横轴相交5.正态曲线下的总面积等于1,即概率值等于16.随机变量的概率由曲线下的面积给出任何一个一般的正态分布,可通过下面的线性变换转化为标准正态分布:标准正态分布表的使用:1.先将一个一般正态分布转换为标准正态分布2.计算概率时,查标准正态概率分布表3.对于负的x,可由F(-x)1=-F(x)得到4.对于标准正态分布,即X~N(0,12),有P(a£X£b)=F(b)-F(a)P(|X|£a)=2F(a)-15.对于一般正态分布,即X~N(m,s2),有:正态分布理论在体育中的应用:一:应用正态分布理论制定考核标准制定考核标准的步骤:1:制作正态曲线的分布草图。2:计算出从﹣∞到ui值所围成的面积概率。3:查表求得各等级的ui值。4:求得各等级标准的原始成绩xi值。举例说明(如书本例5.1)二:应用正态分布理论制定离差评价表制定离差评价表的步骤:专业技术分享\nWORD格式可编辑1:根据指标总数画好框表。2:将各个指标的平均数填入0标准差等级线与各个指标纵线的交叉处。3:计算1标准差,2标准差,3标准差的对应指标数值,并填入各级标准差等级线与各个指标纵线的交叉处。特别要注意计量的方向性(如:田径中田赛与径赛的计分区别)。4:依据指标成绩基础值和指标变化值画出不同时期的变化图线。5:注意离差等级的划分标准合理制定。(参考标准有两种)举例说明(如书本例5.2)三:应用正态分布理论进行人数估算应用正态分布理论进行人数估算的步骤:1:作正态分布曲线的草图,以确定估计范围。2:求各个区间的ui值。3:查表找到所估计范围的面积概率。4:计算估计范围的人数。举例说明(如书本例5.3)四:在综合评价中统一变量单位•U分法:就是依据距离平均数有多少个标准差的距离来确定分数的方法。如果距离平均数在正方向有2个标准差的距离,则记为U分为2分。在负方向有2个标准差距离,则记为U分为-2分。直接用u值来评分。•Z分法:是通过U分转换成更加符合实际运用情况的分数计量方法。可以转换为百分计分法,公式为:•累计计分法:用于符合正态分布的前提下不等距升分的方法之一。其公式为:•百分位数法:用于不符合正态分布的条件下使用变换分数的变量标准化法。其公式见教材P99(5.15)。专业技术分享\nWORD格式可编辑假设检验的基本步骤:(1)根据实际情况建立原假设H0,备择假设H1(2)选择并计算检验统计量的取值(3)确定显著性水平α,查表得出相应的临界值(4)把实值与临界值进行比较,作出统计判断假设检验的几个理论问题一:假设检验的基础(1)逻辑基础:反证法(2)数理统计基础:小概率事件原理二:显著性水平问题(小概率事件发生的概率)一般统计学用到的:α=0.05或者α=0.01三:临界值问题(见置信区间部分内容)两种检验类型一:双侧检验——只是强调差异性,不强调方向性二:单侧检验——研究目的着重强调方向性的,有一定理论和经验基础作为背景假设检验中的两类错误•1.第一类错误(错否定,弃真错误)–原假设为真时拒绝原假设–第一类错误的概率为a,被称为显著性水平•2.第二类错误(错接受,取伪错误)–原假设为假时接受原假设–第二类错误的概率为bU检验专业技术分享\nWORD格式可编辑专业技术分享\nWORD格式可编辑t检验性质:常用于均数的假设检验种类:单样本t检验;独立样本t检验;配对样本t检验一:单样本t检验•检验比较的对象:样本均数与一个已知的总体均数•检验比较的目的:推断样本所代表的未知总体均数μ与已知的总体均数μ0是否相等。(μ=μ0)•例子:“全民健身工程”国民体质检测测试中,已知我国健康成年男子脉搏均数为72次/分,某调研人员在一个山区随机调查了n名健康成年男子的脉搏数(具体原始调研数据已知),能否据此认为该山区成年男子的脉搏数就是(或“就可以代表”)我国健康成年男子脉搏数。二:独立样本t检验专业技术分享\nWORD格式可编辑•检验比较的对象:来自两个正态总体且相互独立的两个样本均数•检验比较的目的:推断两个样本所代表的总体均数μ1与μ2是否相等。(μ1=μ2)•例子:“全民健身工程”国民体质检测测试中,A调研人员在一个a山区随机调查了n1名健康成年男子的脉搏数(具体原始调研数据已知),B调研人员在另一b山区随机调查了n2名健康成年男子的脉搏数(具体原始调研数据也已知),能否据此推断两山区健康成年男子的脉搏数没有差异。或者说能否推断两山区健康成年男子的脉搏数同属于一个共同的大总体的两个样本(即来源于同一总体)。三:配对样本t检验•检验比较的对象:两组数据均能配对的样本•检验比较的目的:比较经不同实验处理后或某因素变化后配对单位的差异是否显著。(μd=0)•例子:某调研人员在一个山区随机调查了n名健康成年男子的脉搏数(具体原始调研数据已知),现在该调研人员对这n人进行了为期三个月的高原体能训练,三个月后再测得了这n名健康成年男子的脉搏数(具体数据已知),想了解这三个月的训练后,这n名健康成年男子的脉搏数是否有了显著性的变化。专业技术分享查看更多