- 2022-08-24 发布 |
- 37.5 KB |
- 10页


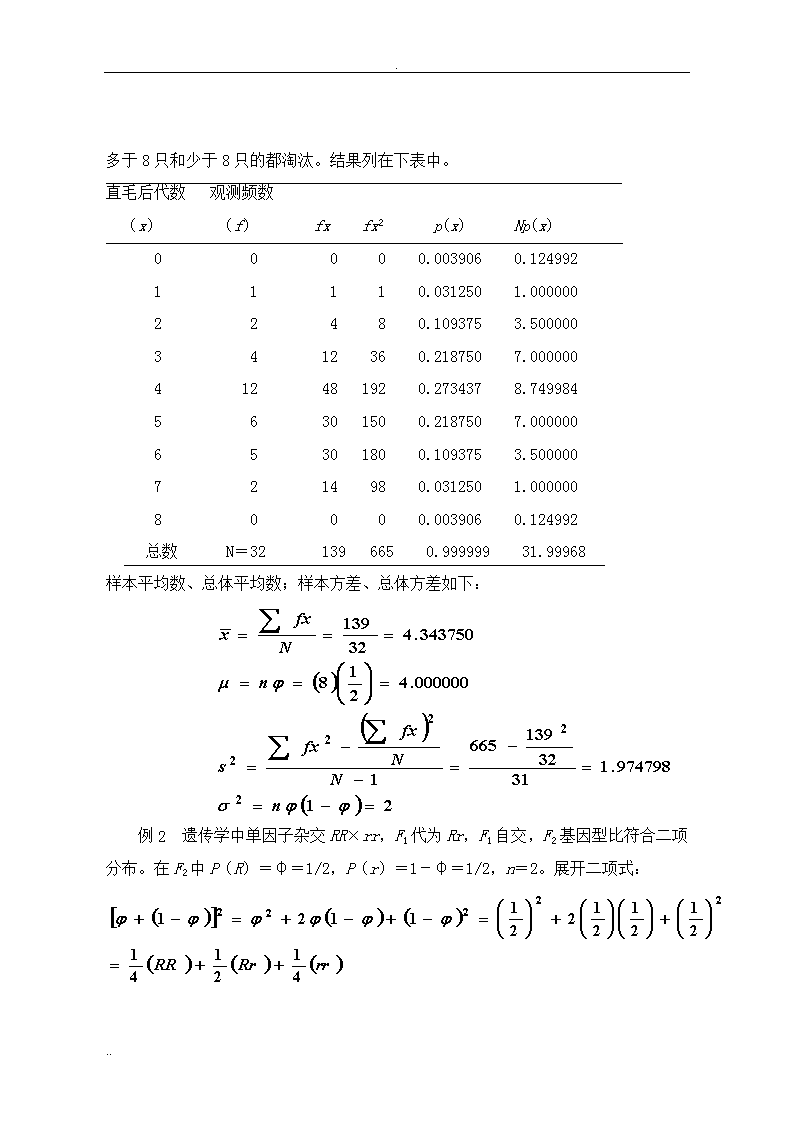
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
生物统计学教案(3)
.生物统计学教案第三章几种常见的概率分布律教学时间:3学时教学方法:课堂板书讲授教学目的:重点掌握正态分布,掌握二项分布,了解泊松分布,中心极限定律。讲授难点:正态分布、二项分布3.1二项分布(重点)3.1.1二项分布的概率函数满足二项分布的条件:1、在一随机试验中,每次试验都有两种不同的结果。2、两种结果是互不相容的。3、每一种结果在每次试验中都有恒定的概率。4、试验间应是独立的。独立地将此试验重复n次,求在n此试验中,一种结果出现x次的概率是多少?例:从雌雄各半的100只动物中抽样,抽样共进行10次,问其中包括3只雄性动物的概率是多少?包括3只及3只以下的概率是多少?即求P(X=3)和P(X≤3)该例符合二项分布的条件。规定以下一组符号:n=试验次数x=在n次试验中事件A出现的次数φ=事件A发生的概率(每次试验都是恒定的)1-φ=事件发生的概率p(x)=x的概率函数=P(X=x)..\n.(累积分布函数)F(x)=P(X≤x)上例中:n=10x=3φ=0.5求p(3)和F(3)。在一次抽样中抽到的结果为:mmmfffffff,它的概率为P(mmmfffffff)=φ3(1-φ)7抽到3雄7雌的数目相当于从10个元素中抽出3个元素的组合数对于任意n和x有以下通式:上式称为二项分布的概率函数。该式正是二项展开式的第x+1项,因而产生“二项分布”这一名称。因为φ+(1-φ)=1,所以将x=0,1,2,3,代入二项分布概率函数,可以得出出现0,1,2,3只雄性动物的概率。P(0)=0.0009766P(1)=0.0097656P(2)=0.0439453P(3)=0.1171876抽到3只和3只以下雄性动物的概率为:F(3)=P(0)+P(1)+P(2)+P(3)=0.17187513.1.2服从二项分布的随机变量的特征数平均数:μ=nφ或μ=φ方差:σ2=nφ(1-φ)或3.1.3二项分布应用实例例1..\n.以杂合基因型Wvwv的小鼠为父本,隐性纯合子小鼠wvwv为母本杂交(wv波浪毛,Wv直毛),后代两种基因型的数目应各占一半。实验只选每窝8只的,多于8只和少于8只的都淘汰。结果列在下表中。直毛后代数观测频数(x)(f)fxfx2p(x)Np(x)00000.0039060.12499211110.0312501.00000022480.1093753.5000003412360.2187507.000000412481920.2734378.74998456301500.2187507.00000065301800.1093753.5000007214980.0312501.00000080000.0039060.124992总数N=321396650.99999931.99968样本平均数、总体平均数;样本方差、总体方差如下:例2遗传学中单因子杂交RR×rr,F1代为Rr,F1自交,F2基因型比符合二项分布。在F2中P(R)=φ=1/2,P(r)=1-φ=1/2,n=2。展开二项式:..\n.对于两对因子,n=4在为人类或动物遗传学研究中,为了保证实验顺利完成,在制定试验计划时,首先要以指定概率求出所需样本含量n。例3用棕色正常毛(bbRR)的家兔和黑色短毛(BBrr)兔杂交,F1代为黑色正常毛长的家兔(BbRr),F1代自交,F2代表型比为:9/16B_R_:3/16B_rr:3/16bbR_:1/16bbrr。问最少需要多少F2代家兔,才能以99%的概率得到一个棕色短毛兔?答:φn=(15/16)n=0.01n(lg15-lg16)=lg0.01-0.02803n=-2.00000n=71.43.2泊松分布3.2.1泊松分布的概率函数在二项分布中,当某事件出现的概率特别小(φ→0),而样本含量又很大(n→∞)时,二项分布就变成泊松分布了。泊松分布是描述在一定空间、长度、面积、体积或一定时间间隔内,点子散布状况的理想化模型。泊松分布的概率函数为:3.2.2服从泊松分布的随机变量的特征数泊松分布的平均数:μ=μ可见,泊松分布的平均数就是泊松分布概率函数中的μ。泊松分布的方差:σ2=μ概率函数中的μ不但是它的平均数,而且是它的方差。..\n.3.2.3泊松分布应用实例例1在麦田中,平均每10m2有一株杂草,问每100m2麦田中,有0株、1株、2株、…杂草的概率是多少?解:先求出每100m2麦田中,平均杂草数μμ=100/10=10株将μ代入泊松分布的概率分布函数中,p(x)=10x/x!e10,即可求出x=0,1,2,…时所相应的概率。结果如下:x≤5678910p(x)0.06710.06310.09010.11260.12510.125111121314≥150.11370.09480.07290.05210.0835例2绘制遗传连锁图时,制图函数是通过泊松分布推演出的。在一对同源染色体之间交换的出现是服从泊松分布的,将x=0代入泊松分布的概率函数中,得出两基因座之间无交换出现的概率。两基因座之间至少出现一次交换的概率P(x≥1)=1-e-μ。从遗传学理论可知,在两基因座之间大于等于1的任何有限次交换其重组频率恒等于50%。因此重组率解出两基因座之间的平均交换次数μ=-ln(1-2RF)两基因座之间平均交换一次,其图距为50m.u.,从而可以得出图距MD=-50ln(1-2RF)..\n.3.4正态分布(重点)3.4.1正态分布的密度函数和分布函数对于平均数是μ,标准差是σ的正态分布,其密度函数为:正态分布密度函数的图象称为正态曲线正态分布曲线以符号N(μ,σ2)表示平均数为μ,标准差为σ2的正态分布。随机变量X的值落在任意区间(a,b)内的概率累积分布函数3.4.2标准正态分布当μ=0,σ=1时的正态分布称为标准正态分布,标准正态分布记为N(0,1)。标准正态分布的密度函数为:..\n.标准正态分布的分布曲线如下图标准正态分布曲线累积分布函数分布图如下:标准正态分布的累积分布曲线标准正态分布有以下特性:1、在u=0时φ(u)达到最大值。2、当u不论向哪个方向远离0时,φ(u)的值都减小。3、曲线两侧对称。4、曲线在u=-1和u=1处有两个拐点。5、曲线与横轴所夹面积等于1。6、累积分布曲线围绕点(0,0.5)对称。..\n.3.4.3正态分布表的查法为了简化计算,随机变量(U)的值(u)落在区间(a,b)内的概率,根据标准正态累积分布函数,已经把不同u值的Ф(u)值列成表(附表2),称为正态分布表。根据以下关系式可以扩展正态分布表的使用范围。例1查u=-0.82及u=1.15时的Ф(u)值。解:Ф(-0.82)=0.20611Ф(1.15)=0.87493例2随机变量U服从正态分布N(0,1),问随机变量的值落在0,1.21间的概率是多少?落在-1.96,1.96间的概率是多少?解:1)P(0查看更多