- 2022-08-19 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数理经济学08-计量经济学有关问题new
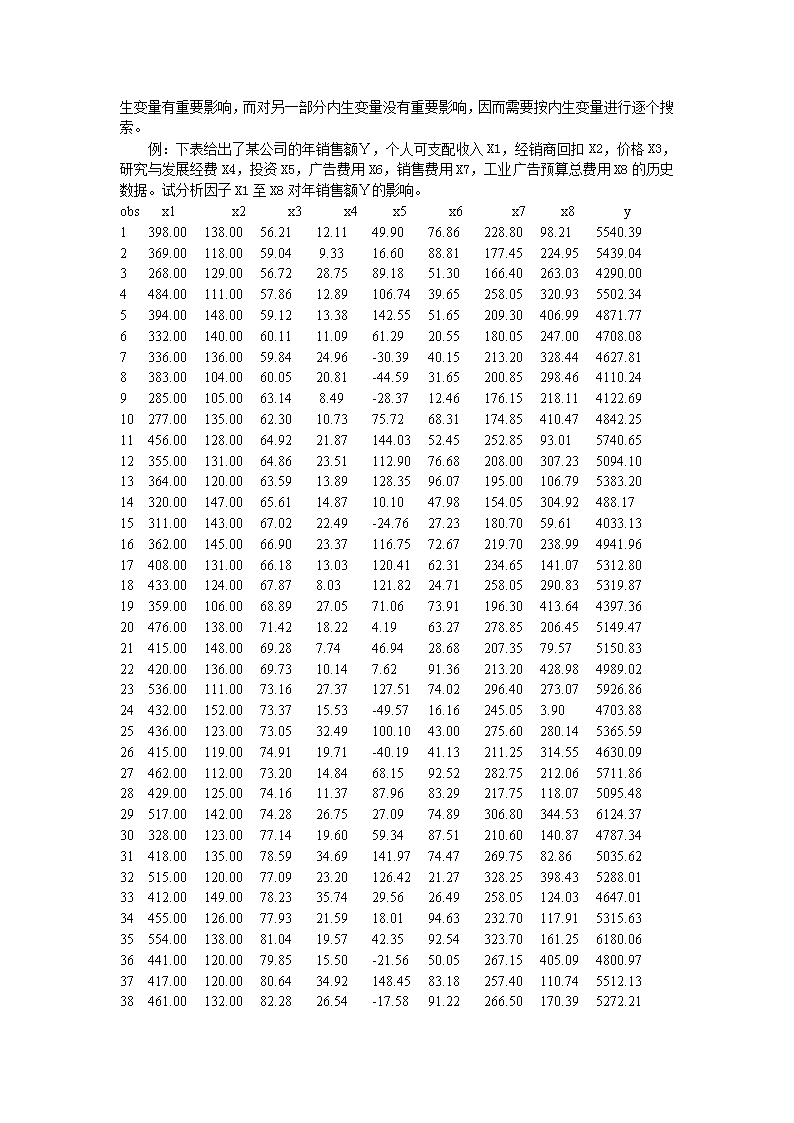
第七章计量经济学应用§7.1计量经济学模型的设定计量经济学模型设定的主要根据:1)研究目的;2)已有理论模型。通常是根据研究目的所涉及的范围,决定需要分析哪些经济变量之间的关系。再设定这些变量之间的关系式。设定变量关系式可以根据已有的理论模型、经济恒等式、经济关系式来确定(可能需要进行一定的修改)。若没有已知的关系式可用,可以根据研究目的,人为设定。变量间具体表达式的选择若经济理论已给出具体表达式,就直接套用。否则,可以直接假设为线性函数。其原因是经济中的所使用函数大多数都认为是连续可微的函数,因而可以用线性函数近似。§7.2数据调整由于统计指标与经济变量的含义、口径一般不会一致。在模型估计之前,如有可能,应先进行调整,使统计指标的口径尽可能的接近经济变量的含义。§7.3变量的选择基于上述同样的原因,及统计指标间的相关性,在设计模型结构时,需要筛选变量。假设模型已转化为简化型,即设模型为变量筛选有两层含义:1)对内生变量有重要影响的外生变量是否都选入模型了?2)模型内的外生变量对内生变量是否都有重要影响?判别准则1)复相关系数R(一般要求R>0.8),或方程的F-统计量;一般来说,若R>0.9或经F-检验是显著的,则从整体上说,方程几乎包含了对响应变量有重要影响所有外生变量,外生变量对内生变量有较强的解释能力,否则,表明方程遗漏了一些对内生变量有重要影响的变量,需要增加外生变量。当模型用于结构分析时,R值可以低一些,用于预测时,R值应比较大。\n1)系数显著性检验t-统计量。下面介绍几种常用的变量筛选算法。这些算法都是一对多回归模型的搜索算法。记是在回归模型内的预测变量集,是在回归模型外待检的预测变量集,是已剔除的预测变量集,1、前向回归法从仅含一个预测变量的模型开始,逐步将有显著影响的预测变量加入到模型中去,直至检查完所有的预测变量。该算法基本过程描述如下:1)令,,;2)取,将它加入;3)在上做回归,检查的显著性,若不显著,则将剔除,并将它送入;若是显著的,则将它保留在内;4)若,则转向2),否则,停止筛选过程。2、后向回归法从含有所有预测变量的回归模型开始,一次剔除一个最不显著的预测变量,直至没有预测变量可以被剔除。该算法的基本过程描述如下:1)令,,;2)在上做回归,检查的显著性;若所有的都是显著的,则停止筛选过程;否则,转向下一步;3)选择最不显著的,将其剔除,并加入到,转向2)。上述两个算法,外生变量被保留或被删除依赖于变量加入的顺序。3、逐步回归法该算法是前向和后向回归的综合。它先执行前向回归,只是在加入每一个新预测变量后,在执行一次后向回归过程。该算法的基本过程描述如下:1)令,,;2)取,将它加入;3)在上做后向回归,将不显著的预测变量逐个从剔除,并放回,直至到中没有变量可以被剔除;4)若,则转向2),否则,停止筛选过程。\n在变量搜索中,多对多回归与一对多回归的主要差异在于某些外生变量可能只对部分内生变量有重要影响,而对另一部分内生变量没有重要影响,因而需要按内生变量进行逐个搜索。例:下表给出了某公司的年销售额Y,个人可支配收入X1,经销商回扣X2,价格X3,研究与发展经费X4,投资X5,广告费用X6,销售费用X7,工业广告预算总费用X8的历史数据。试分析因子X1至X8对年销售额Y的影响。obsx1x2x3x4x5x6x7x8y1398.00138.0056.2112.1149.9076.86228.8098.215540.392369.00118.0059.049.3316.6088.81177.45224.955439.043268.00129.0056.7228.7589.1851.30166.40263.034290.004484.00111.0057.8612.89106.7439.65258.05320.935502.345394.00148.0059.1213.38142.5551.65209.30406.994871.776332.00140.0060.1111.0961.2920.55180.05247.004708.087336.00136.0059.8424.96-30.3940.15213.20328.444627.818383.00104.0060.0520.81-44.5931.65200.85298.464110.249285.00105.0063.148.49-28.3712.46176.15218.114122.6910277.00135.0062.3010.7375.7268.31174.85410.474842.2511456.00128.0064.9221.87144.0352.45252.8593.015740.6512355.00131.0064.8623.51112.9076.68208.00307.235094.1013364.00120.0063.5913.89128.3596.07195.00106.795383.2014320.00147.0065.6114.8710.1047.98154.05304.92488.1715311.00143.0067.0222.49-24.7627.23180.7059.614033.1316362.00145.0066.9023.37116.7572.67219.70238.994941.9617408.00131.0066.1813.03120.4162.31234.65141.075312.8018433.00124.0067.878.03121.8224.71258.05290.835319.8719359.00106.0068.8927.0571.0673.91196.30413.644397.3620476.00138.0071.4218.224.1963.27278.85206.455149.4721415.00148.0069.287.7446.9428.68207.3579.575150.8322420.00136.0069.7310.147.6291.36213.20428.984989.0223536.00111.0073.1627.37127.5174.02296.40273.075926.8624432.00152.0073.3715.53-49.5716.16245.053.904703.8825436.00123.0073.0532.49100.1043.00275.60280.145365.5926415.00119.0074.9119.71-40.1941.13211.25314.554630.0927462.00112.0073.2014.8468.1592.52282.75212.065711.8628429.00125.0074.1611.3787.9683.29217.75118.075095.4829517.00142.0074.2826.7527.0974.89306.80344.536124.3730328.00123.0077.1419.6059.3487.51210.60140.874787.3431418.00135.0078.5934.69141.9774.47269.7582.865035.6232515.00120.0077.0923.20126.4221.27328.25398.435288.0133412.00149.0078.2335.7429.5626.49258.05124.034647.0134455.00126.0077.9321.5918.0194.63232.70117.915315.6335554.00138.0081.0419.5742.3592.54323.70161.256180.0636441.00120.0079.8515.50-21.5650.05267.15405.094800.9737417.00120.0080.6434.92148.4583.18257.40110.745512.1338461.00132.0082.2826.54-17.5891.22266.50170.395272.21\n§7.4时间序列模型常见的时间序列模型有AR或VAR模型、MA模型、ARMA模型、ARIMA模型。但在宏观经济分析中,用得最多的是AR或VAR模型。在建立AR或VAR模型在时,最关键的是确定AR或VAR模型的阶数。在时间序列教程中,介绍了许多确定阶的方法,最常见,也最复杂的是Box-Jenkins方法。但是,我们也可以用上面讲的逐步回归方法。首先,根据经验,确定AR或VAR模型的一个可能的最大阶数p。视为外生变量,为内生变量,然后,执行逐步回归,筛选变量,直至算法结束。最后保留的最大阶数为所求的阶数。例:下表是某地区1970-192年的物价数据。其中,第一列是时间变量(obs),第二列至第六列依次是社会零售价格总指数(X1)、农副产品收购价格总指数(X2)、城镇职工生活费用指数(X3)、农村工业品零售价格指数(X4)、工农产品价格比价(X5)。试建立X2、X3、X4、X5对X2、X3、X4、X5的向量自回归时间序列模型。X1X2X3X4X51970131.5000195.1000137.8000111.900057.400001971130.5000198.3000137.7000110.200055.600001972130.2000201.1000137.9000109.600054.500001973131.0000202.8000138.0000109.600054.000001974131.7000204.5000138.9000109.600053.600001975131.9000208.7000139.5000109.600052.500001976132.3000209.7000139.9000109.700052.300001977135.0000209.2000143.7000109.800052.500001978135.9000217.4000144.7000109.800050.500001979138.6000265.5000147.4000109.800041.400001980146.9000284.4000158.5000110.800039.000001981150.4000301.2000162.5000111.900037.200001982153.3000307.8000165.8000113.700036.900001983155.6000321.3000169.1000114.800035.700001984160.0000334.2000173.7000118.400035.400001985174.1000362.9000194.4000122.200033.700001986184.5000386.1000208.0000126.100032.700001987198.0000432.4000226.3000132.200030.600001988234.6000531.9000273.1000152.300028.600001989276.4000611.7000317.6000180.800029.60000\n1990282.2000595.8000321.7000189.100031.700001991290.4000583.9000338.1000194.800033.400001992306.1000603.8000367.2000200.800033.30000用这种方法建立的AR或VAR模型具有下列性质:1.由于本算法总是强迫对Yt-q-1的分量进行搜索,这样通常能有效地防止因低阶项已进入模型而阻止高阶项不能进入模型的情况发生,从而能得到一个较好的阶数估计值。2.用本算法得到的VAR模型是一个节省参数模型。3.本算法是递推的,故计算工作量较小。4.为了保证本算法有足够的初值可用,应事先指定一个模型阶数的上限。§7.5两类模型的比较回归模型:适用于结构分析;时间序列:适用于短期预测。对于VAR模型,可以进行因果关系分析。查看更多