大学物理(下册)答案[1]

大学物理(下册)答案[1]

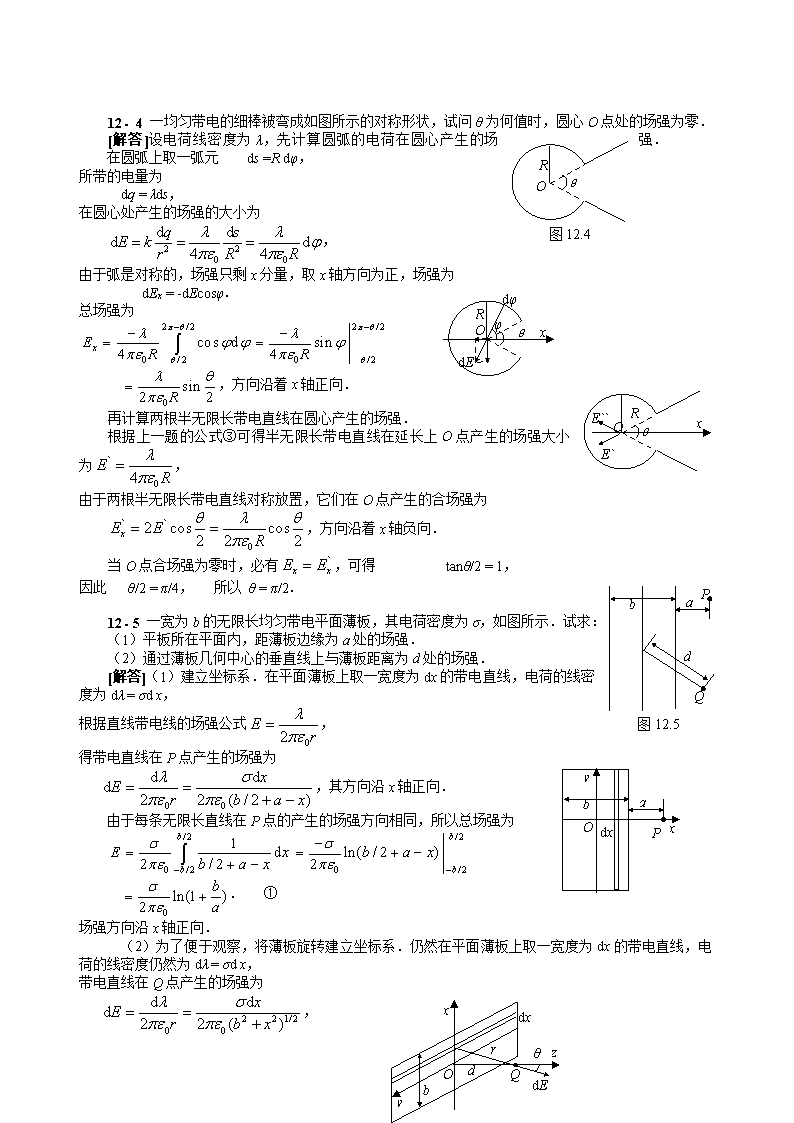
大学物理习题集(下册)第十二章真空中的静电场12．1如图所示，在直角三角形ABCD的A点处，有点电荷q1=1.8×10-9C，B点处有点电荷q2=-4.8×10-9C，AC=3cm，BC=4cm，试求C点的场强．E2EE1q2ACq1Bθ图12.1[解答]根据点电荷的场强大小的公式，其中1/(4πε0)=k=9.0×109N·m2·C-2．点电荷q1在C点产生的场强大小为：方向向下．点电荷q2在C点产生的场强大小为，方向向右．C处的总场强大小为，总场强与分场强E2的夹角为．12．2半径为R的一段圆弧，圆心角为60°，一半均匀带正电，另一半均匀带负电，其电线密度分别ExxEθRdsEyOy为+λ和-λ，求圆心处的场强．[解答]在带正电的圆弧上取一弧元ds=Rdθ，电荷元为dq=λds，在O点产生的场强大小为，场强的分量为dEx=dEcosθ，dEy=dEsinθ．对于带负电的圆弧，同样可得在O点的场强的两个分量．由于弧形是对称的，x方向的合场强为零，总场强沿着y轴正方向，大小为dsExxEθREyOy．12．3均匀带电细棒，棒长a=20cm，电荷线密度为λ=3×10-8C·m-1，求：（1）棒的延长线上与棒的近端d1=8cm处的场强；（2）棒的垂直平分线上与棒的中点相距d2=8cm处的场强．[解答]（1）建立坐标系，其中L=a/2=0.1(m)，x=L+d1=0.18(m)．olxxdlyP1r-LLd1在细棒上取一线元dl，所带的电量为dq=λdl，根据点电荷的场强公式，电荷元在P1点产生的场强的大小为\n场强的方向沿x轴正向．因此P1点的总场强大小通过积分得．①将数值代入公式得P1点的场强为=2.41×103(N·C-1)，olxxdlr-LLyP2dEydE2dExd2θθ方向沿着x轴正向．（2）建立坐标系，y=d2．在细棒上取一线元dl，所带的电量为dq=λdl，在棒的垂直平分线上的P2点产生的场强的大小为，由于棒是对称的，x方向的合场强为零，y分量为dEy=dE2sinθ．由图可知：r=d2/sinθ，l=d2cotθ，所以dl=-d2dθ/sin2θ，因此，总场强大小为．②将数值代入公式得P2点的场强为=5.27×103(N·C-1)．方向沿着y轴正向．[讨论]（1）由于L=a/2，x=L+d1，代入①式，化简得，保持d1不变，当a→∞时，可得，③这就是半无限长带电直线在相距为d1的延长线上产生的场强大小．（2）由②式得，当a→∞时，得，④这就是无限长带电直线在线外产生的场强公式．如果d1=d2，则有大小关系Ey=2E1．\n12．4一均匀带电的细棒被弯成如图所示的对称形状，试问θ为何值时，圆θRO图12.4心O点处的场强为零．[解答]设电荷线密度为λ，先计算圆弧的电荷在圆心产生的场强．在圆弧上取一弧元ds=Rdφ，所带的电量为dq=λds，在圆心处产生的场强的大小为，由于弧是对称的，场强只剩x分量，取x轴方向为正，场强为θROxdφdEφdEx=-dEcosφ．总场强为θOE`E``xR，方向沿着x轴正向．再计算两根半无限长带电直线在圆心产生的场强．根据上一题的公式③可得半无限长带电直线在延长上O点产生的场强大小为，由于两根半无限长带电直线对称放置，它们在O点产生的合场强为，方向沿着x轴负向．当O点合场强为零时，必有，可得tanθ/2=1，PbaQd图12.5因此θ/2=π/4，所以θ=π/2．12．5一宽为b的无限长均匀带电平面薄板，其电荷密度为σ，如图所示．试求：（1）平板所在平面内，距薄板边缘为a处的场强．（2）通过薄板几何中心的垂直线上与薄板距离为d处的场强．[解答]（1）建立坐标系．在平面薄板上取一宽度为dx的带电直线，电荷的线密度为dλ=σdx，根据直线带电线的场强公式，PbaOxdxy得带电直线在P点产生的场强为，其方向沿x轴正向．由于每条无限长直线在P点的产生的场强方向相同，所以总场强为．①场强方向沿x轴正向．（2）为了便于观察，将薄板旋转建立坐标系．仍然在平面薄板上取一宽度为dx的带电直线，电荷的线密度仍然为dλ=σdx，带电直线在Q点产生的场强为QbdOzdxxyrdEθ，\n沿z轴方向的分量为，设x=dtanθ，则dx=ddθ/cos2θ，因此积分得．②场强方向沿z轴正向．[讨论]（1）薄板单位长度上电荷为λ=σb，①式的场强可化为，当b→0时，薄板就变成一根直线，应用罗必塔法则或泰勒展开式，场强公式变为，③这正是带电直线的场强公式．（2）②也可以化为，当b→0时，薄板就变成一根直线，应用罗必塔法则或泰勒展开式，场强公式变为，这也是带电直线的场强公式．当b→∞时，可得：，④这是无限大带电平面所产生的场强公式．12．6（1）点电荷q位于一个边长为a的立方体中心，试求在该点电荷电场中穿过立方体一面的电通量是多少？（2）如果将该场源点电荷移到立方体的的一个角上，这时通过立方体各面的电通量是多少？[解答]点电荷产生的电通量为Φe=q/ε0．（1）当点电荷放在中心时，电通量要穿过6个面，通过每一面的电通量为Φ1=Φe/6=q/6ε0．（2）当点电荷放在一个顶角时，电通量要穿过8个卦限，立方体的3个面在一个卦限中，通过每个面的电通量为Φ1=Φe/24=q/24ε0；立方体的另外3个面的法向与电力线垂直，通过每个面的电通量为零．12．7面电荷密度为σ的均匀无限大带电平板，以平板上的一点O为中心，R为半径作一半球面，RO如图所示．求通过此半球面的电通量．[解答]设想在平板下面补一个半球面，与上面的半球面合成一个球面．球面内包含的电荷为q=πR2σ，通过球面的电通量为图12.7Φe=q/ε0，通过半球面的电通量为Φ`e=Φe/2=πR2σ/2ε0．12．8两无限长同轴圆柱面，半径分别为R1和R2(R1>R2)，带有等量异号电荷，单位长度的电量为λ和-λ，求（1）rR2处各点的场强．[解答]由于电荷分布具有轴对称性，所以电场分布也具有轴对称性．（1）在内圆柱面内做一同轴圆柱形高斯面，由于高斯内没有电荷，所以\nE=0，（rR2）．S2S1E`S1S2EEd2rS0E`S012．9一厚度为d的均匀带电无限大平板，电荷体密度为ρ，求板内外各点的场强．[解答]方法一：高斯定理法．（1）由于平板具有面对称性，因此产生的场强的方向与平板垂直且对称于中心面：E=E`．在板内取一底面积为S，高为2r的圆柱面作为高斯面，场强与上下两表面的法线方向平等而与侧面垂直，通过高斯面的电通量为，高斯面内的体积为V=2rS，包含的电量为q=ρV=2ρrS，根据高斯定理Φe=q/ε0，可得场强为E=ρr/ε0，(0≦r≦d/2)．①（2）穿过平板作一底面积为S，高为2r的圆柱形高斯面，通过高斯面的电通量仍为Φe=2ES，高斯面在板内的体积为V=Sd，包含的电量为q=ρV=ρSd，根据高斯定理Φe=q/ε0，可得场强为E=ρd/2ε0，(r≧d/2)．②方法二：场强叠加法．（1）由于平板的可视很多薄板叠而成的，以r为界，下面平板产生E2dyryoE1d的场强方向向上，上面平板产生的场强方向向下．在下面板中取一薄层dy，面电荷密度为dσ=ρdy，产生的场强为dE1=dσ/2ε0，积分得，③同理，上面板产生的场强为，④r处的总场强为E=E1-E2=ρr/ε0．（2）在公式③和④中，令r=d/2，得E2=0、E=E1=ρd/2ε0，E就是平板表面的场强．平板外的场强是无数个无限薄的带电平板产生的电场叠加的结果，是均强电场，方向与平板垂直，大小等于平板表面的场强，也能得出②式．12．10一半径为R的均匀带电球体内的电荷体密度为ρ，若在球内挖去一块半径为R`>R2）[证明]方法一：并联电容法．在外球外面再接一个半径为R3大外球壳，外壳也接地．内球壳和外球壳之间是一个电容器，电容为外球壳和大外球壳之间也是一个电容器，电容为．外球壳是一极，由于内球壳和大外球壳都接地，共用一极，所以两个电容并联．当R3趋于无穷大时，C2=4πε0R2．并联电容为．方法二：电容定义法．假设外壳带正电为q，则内壳将感应电荷q`．内球的电势是两个电荷产生的叠加的结果．由于内球接地，所以其电势为零；由于内球是一个等势体，其球心的电势为，因此感应电荷为．根据高斯定理可得两球壳之间的场强为，负号表示场强方向由外球壳指向内球壳．取外球壳指向内球壳的一条电力线，两球壳之间的电势差为球面间的电容为．13．8球形电容器的内、外半径分别为R1和R2，其间一半充满相对介电常量为oR2R1εr图13.8εr的均匀电介质，求电容C为多少？[解答]球形电容器的电容为．对于半球来说，由于相对面积减少了一半，所以电容也减少一半：．当电容器中充满介质时，电容为：．由于内球是一极，外球是一极，所以两个电容器并联：．13．9设板面积为S的平板电容器析板间有两层介质，介电常量分别为ε1和ε2，厚度分别为d1和d2，d2ε1ε2d1图13.9求电容器的电容．\n[解答]假设在两介质的介面插入一薄导体，可知两个电容器串联，电容分别为C1=ε1S/d1和C2=ε2S/d2．总电容的倒数为，总电容为．13．10圆柱形电容器是由半径为R1的导线和与它同轴的内半径为R2的导体圆筒构成的，其长为l，其间充满了介电常量为ε的介质．设沿轴线单位长度导线上的电荷为λ，圆筒的电荷为-λ，略去边缘效DS1S2S0rR2R1εl应．求：（1）两极的电势差U；（2）介质中的电场强度E、电位移D；（3）电容C，它是真空时电容的多少倍？[解答]介质中的电场强度和电位移是轴对称分布的．在内外半径之间作一个半径为r、长为l的圆柱形高斯面，侧面为S0，上下两底面分别为S1和S2．通过高斯面的电位移通量为，高斯面包围的自由电荷为q=λl，根据介质中的高斯定理Φd=q，可得电位为D=λ/2πr，方向垂直中心轴向外．电场强度为E=D/ε=λ/2πεr，方向也垂直中心轴向外．取一条电力线为积分路径，电势差为．电容为．在真空时的电容为，所以倍数为C/C0=ε/ε0．13．11在半径为R1的金属球外还有一层半径为R2的均匀介质，相对介电常量为εr．设金属球带电Q0，求：（1）介质层内、外D、E、P的分布；（2）介质层内、外表面的极化电荷面密度．[解答]（1）在介质内，电场强度和电位移以及极化强度是球对称分布的．在内外半径之间作一个半径为r的球形高斯面，通过高斯面的电位移通量为高斯面包围的自由电荷为q=Q0，根据介质中的高斯定理Φd=q，可得电位为D=Q0/4πr2，方向沿着径向．用矢量表示为D=Q0r/4πr3．电场强度为E=D/ε0εr=Q0r/4πε0εrr3，方向沿着径向．由于　　D=ε0E+P，所以P=D-ε0E=．在介质之外是真空，真空可当作介电常量εr=1的介质处理，所以D=Q0r/4πr3，E=Q0r/4πε0r3，P=0．（2）在介质层内靠近金属球处，自由电荷Q0产生的场为E0=Q0r/4πε0r3；极化电荷q1`产生的场强为E`=q1`r/4πε0r3；\n总场强为E=Q0r/4πε0εrr3．由于E=E0+E`，解得极化电荷为，介质层内表面的极化电荷面密度为．在介质层外表面，极化电荷为，面密度为．13．12两个电容器电容之比C1:C2=1:2，把它们串联后接电源上充电，它们的静电能量之比为多少？如果把它们并联后接到电源上充电，它们的静电能之比又是多少？[解答]两个电容器串联后充电，每个电容器带电量是相同的，根据静电能量公式W=Q2/2C，得静电能之比为W1:W2=C2:C1=2:1．两个电容器并联后充电，每个电容器两端的电压是相同的，根据静电能量公式W=CU2/2，得静电能之比为W1:W2=C1:C2=1:2．13．13一平行板电容器板面积为S，板间距离为d，接在电源上维持其电压为U．将一块厚度为d相对介电常量为εr的均匀介电质板插入电容器的一半空间内，求电容器的静电能为多少？[解答]平行板电容器的电容为C=ε0S/d，当面积减少一半时，电容为C1=ε0S/2d；另一半插入电介质时，电容为C2=ε0εrS/2d．两个电容器并联，总电容为C=C1+C2=(1+εr)ε0S/2d，静电能为W=CU2/2=(1+εr)ε0SU2/4d．13．14一平行板电容器板面积为S，板间距离为d，两板竖直放着．若电容器两板充电到电压为U时，断开电源，使电容器的一半浸在相对介电常量为εr的液体中．求：（1）电容器的电容C；（2）浸入液体后电容器的静电能；（3）极板上的自由电荷面密度．[解答]（1）如前所述，两电容器并联的电容为C=(1+εr)ε0S/2d．（2）电容器充电前的电容为C0=ε0S/d，充电后所带电量为Q=C0U．当电容器的一半浸在介质中后，电容虽然改变了，但是电量不变，所以静电能为W=Q2/2C=C02U2/2C=ε0SU2/(1+εr)d．（3）电容器的一半浸入介质后，真空的一半的电容为C1=ε0S/2d；介质中的一半的电容为C2=ε0εrS/2d．设两半的所带自由电荷分别为Q1和Q2，则Q1+Q2=Q．①由于C=Q/U，所以U=Q1/C1=Q2/C2．②解联立方程得，真空中一半电容器的自由电荷面密度为．同理，介质中一半电容器的自由电荷面密度为．13．15平行板电容器极板面积为200cm2，板间距离为1.0mm，电容器内有一块1.0mm厚的玻璃板(εr=5)．将电容器与300V的电源相连．求：（1）维持两极板电压不变抽出玻璃板，电容器的能量变化为多少？（2）断开电源维持板上电量不变，抽出玻璃板，电容器能量变化为多少？[解答]平行板电容器的电容为C0=ε0εrS/d，静电能为W0=C0U2/2．\n玻璃板抽出之后的电容为C=ε0S/d．（1）保持电压不变抽出玻璃板，静电能为W=CU2/2，电能器能量变化为ΔW=W-W0=(C-C0)U2/2=(1-εr)ε0SU2/2d=-3.18×10-5(J)．（2）充电后所带电量为Q=C0U，保持电量不变抽出玻璃板，静电能为W=Q2/2C，电能器能量变化为=1.59×10-4(J)．13．16设圆柱形电容器的内、外圆筒半径分别为a、b．试证明电容器能量的一半储存在半径的圆柱体内．[解答]设圆柱形电容器电荷线密度为λ，场强为E=λ/2πε0r，能量密度为w=ε0E2/2，体积元为dV=2πrldr，能量元为dW=wdV．在半径a到R的圆柱体储存的能量为．当R=b时，能量为；当时，能量为，所以W2=W1/2，即电容器能量的一半储存在半径的圆柱体内．13．17两个同轴的圆柱面，长度均为l，半径分别为a、b，柱面之间充满介电常量为ε的电介质（忽略边缘效应）．当这两个导体带有等量异号电荷(±Q)时，求：（1）在半径为r(aR2)．（2）在圆柱和圆筒之间离轴线r处作一径向的长为l=1、宽为dr的矩形，其面积为dS=ldr=dr，方向与磁力线的方向一致，通过矩形的磁通量为dΦ=BdS=Bdr，总磁通量为．\n*14．18一长直载流导体，具有半径为R的圆形横截面，在其内部有与导体相切，半径为a的圆柱baRO1O`1图14.18形长孔，其轴与导体轴平行，相距b=R–a，导体截有均匀分布的电流I．（1）证明空孔内的磁场为均匀场并求出磁感应强度B的值；（2）若要获得与载流为I，单位长度匝数n的长螺线管内部磁场相等的均匀磁场，a应满足什么条件？[解答]（1）导体中的电流垂直纸面向外，电流密度为．长孔中没有电流，可以当作通有相反电流的导体，两个电流密度的大小都为δ，这样，长孔中磁场是两个均匀分布的圆形电流产生的．如果在圆形截面中过任意点P取一个半径为r的同心圆，其面积为baRO1O`1rr`BrBBr`θφPS=πr2，包围的电流为ΣI=δS=πr2δ，根据安培环路定理可得方程2πrBr=μ0ΣI，磁感应强度为，方向与矢径r垂直．同理，密度为-δ的电流在P点产生的磁感应强度为，方向与矢径r`垂直．设两个磁感应强度之间的夹角为θ，则合场强的平方为．根据余弦定理，如图可知：，由于φ=π-θ，所以，由于b和δ都是常量，可见：长孔中是均匀磁场．将δ和b代入公式得磁感应强度大小为，可以证明磁场的方向向上．（2）[解答]长螺线管内部的场为B=μ0nI，与上式联立得，这就是a所满足的条件．[注意]此题中的长孔中的磁场与习题13．10．中空腔中的电场情况非常类似．14．19在XOY平面内有一载流线圈abcda，通有电流I=20A，半径R=20cm，电流方向如图所示．线圈处于磁感应强度B=8.0×10-2T的均强磁场中，dcθbIaXRo1αBY图14.19B沿着X轴正方向．求：直线段ab和cd以及圆弧段和在外磁场中所受安培力的大小和方向．[解答]根据右手螺旋法则，弧和cd边受力方向垂直纸面向外，弧和ab边受力方向垂直纸面向里．由于对称的关系，ab边和cd边所受安培力的大小是相同的，弧和弧所受安培力的大小也是相同的．ab边与磁场方向的夹角是α=45°，长度为l=R/sinα，所受安培力为Fab=|Il×B|=IlBsinα=IRB=0.32(N)=Fcd．在圆弧上取一电流元Idl，其矢径R与X轴方向的夹角为θ，所受力的大小为dFbc=|Idl×B|=IdlBsinθ，由于线元为dl=Rdθ，所以dFbc=IRBsinθdθ，因此安培力为=IRB=0.32(N)=Fda．\n14．20载有电流I1的无限长直导线旁有一正三角形线圈，边长为a，载有电流I2，一边与直导线平等且与直导线相距为b，直导线与线圈共面，如图所示，求I1作用在这三角形线圈上的力．[解答]电流I1在右边产生磁场方向垂直纸面向里，在AB边处产生的磁感应强度大小为CI2ybAxao1αBI1图14.20B=μ0I1/2πb，作用力大小为FAB=I2aB=μ0I1I2a/2πb，方向向左．三角形的三个内角α=60°，在AC边上的电流元I2dl所受磁场力为dF=I2dlB，两个分量分别为dFx=dFcosα和dFy=dFsinα，与BC边相比，两个x分量大小相等，方向相同；两个y分量大小相等，方向相反．由于dl=dr/sinα，所以dFx=I2drBcotα，积分得．作用在三角形线圈上的力的大小为F=FAB–2Fx，方向向左．14．21载有电流I1的无限长直导线，在它上面放置一个半径为R电流为I2的圆形电流线圈，长直导线沿其直径方向，且相互绝缘，如图所示．求I2在电流I1的磁场中所受到的力．[解答]电流I1在右边产生磁场方向垂直纸面向里，右上1/4弧受力向右上方，右下1/4弧受力向右下方；电流I1在左边产生磁场方向垂直纸面向外，左上1/4弧受力向右下方，左下1/4弧受力向右上方．因θrI1oRI2图14.21此，合力方向向右，大小是右上1/4弧所受的向右的力的四倍．电流元所受的力的大小为dF=I2dlB，其中dl=Rdθ，B=μ0I1/2πr，而r=Rcosθ，所以向右的分量为dFx=dFcosθ=μ0I1I2dθ/2π，积分得，电流I2所受的合力大小为F=4Fx=μ0I1I2，方向向右．14．22如图所示，斜面上放有一木制圆柱，质量m=0.5kg，半径为R，长为l=0.10m，圆柱上绕有10匝导线，圆柱体的轴线位导线回路平面内．斜面倾角为θ，处于均匀磁场B=0.5T中，B的方向竖直向上．如果线圈平面与斜面平行，求通过回路的电流I至少要多大时，圆柱才不致沿斜面向下滚动？[解答]线圈面积为S=2Rl，θBθoG图14.22磁矩大小为pm=NIS，方向与B成θ角，所以磁力矩大小为Mm=|pm×B|=pmBsinθ=NI2RlBsinθ，方向垂直纸面向外．重力大小为G=mg，力臂为L=Rsinθ，重力矩为Mg=GL=mgRsinθ，方向垂直纸面向里．圆柱不滚动时，两力矩平衡，即NI2RlBsinθ=mgRsinθ，解得电流强度为I=mg/2NlB=5(A)．14．23均匀带电细直线AB，电荷线密度为λ，可绕垂直于直线的轴O以ω角速度均速转动，设直线长为b，其A端距转轴O距离为a，求：（1）O点的磁感应强度B；（2）磁矩pm；BAbωoa图14.23（3）若a>>b，求B0与pm．\n[解答]（1）直线转动的周期为T=2π/ω，在直线上距O为r处取一径向线元dr，所带的电量为dq=λdr，形成的圆电流元为dI=dq/T=ωλdr/2π，在圆心O点产生的磁感应强度为dB=μ0dI/2r=μ0ωλdr/4πr，整个直线在O点产生磁感应强度为，如果λ>0，B的方向垂直纸面向外．（2）圆电流元包含的面积为S=πr2，形成的磁矩为dpm=SdI=ωλr2dr/2，积分得．如果λ>0，pm的方向垂直纸面向外．（3）当a>>b时，因为，所以．．14．24一圆线圈直径为8cm，共12匝，通有电流5A，将此线圈置于磁感应强度为0.6T的均强磁场中，求：（1）作用在线圈上的电大磁力矩为多少？（2）线圈平面在什么位置时磁力矩为最大磁力矩的一半．[解答]（1）线圈半径为R=0.04m，面积为S=πR2，磁矩为pm=NIS=πR2NI，磁力矩为M=pmBsinθ．当θ=π/2时，磁力矩最大Mm=pmB=πR2NIB=0.18(N·m)．（2）由于M=Mmsinθ，当M=Mm/2时，可得sinθ=0.5，θ=30°或150°．I2ROI1图14.25*14．25在半径为R，通以电流I2的圆电流的圆周上，有一无限长通以电流I1的直导线（I1，I2相互绝缘，且I1与圆电流I2所在平面垂直），如图所示，求I2所受的力矩．若I1置于圆电流圆心处（仍垂直），I2所受力矩又如何？[解答]在x轴上方的圆周上取一电流元I2dl，其大小为I2dl=I2Rdθ，所受的安培力为dF=I2dl×B，I2ROI1BI2dlxθφφr其大小为dF=|I2dl×B|=I2RdθBsinφ，其中φ=θ/2，B是电流I1在电流元I2dl处产生的磁感应强度，因此安培力的大小可化为，力的方向垂直纸面向里．如果在x轴下方取一电流元，其受力方向垂直纸面向外，因此，圆周所受的安培力使其绕x轴旋转．I2ROI1B电流元所受的力矩为电流所受的力矩为．如果电流I1置于圆电流圆心处，那么I2就与I1产生的磁力线重合，所受的力为零，力矩也为零．14．26一个电子在B=20×10-4T的磁场中，沿半径R=2cm的螺旋线运动，螺距h=5cm\n，如图所示，求：（1）电子的速度为多少？（2）B的方向如何？[解答]电子带负电，设速度v的方向与磁力线的负方向成θ角，则沿着磁力线方向的速Rh图14.26度为v1=vcosθ，垂直速度为v2=vsinθ．由R=mv2/eB，得v2=eBR/m．由h=v1T，得v1=h/T=heB/2πm，因此速度为=7.75×106(m·s-1)；由=2.51，得θ=68.3°=68°18′．YXy1oBIZz1图14.2714．27一银质条带，z1=2cm，y1=1mm．银条置于Y方向的均匀磁场中B=1.5T，如图所示．设电流强度I=200A，自由电子数n=7.4×1028个·m-3，试求：（1）电子的漂移速度；（2）霍尔电压为多少？[解答]（1）电流密度为δ=ρv，其中电荷的体密度为ρ=ne.电流通过的横截面为S=y1z1，电流强度为I=δS=neSv，得电子的漂移速度为=8.45×10-4(m·s-1)．（2）霍尔系数为=8.44×10-11(m3·C-1)，霍尔电压为=2.53×10-5(V)．第十五章磁介质的磁化15．1一均匀磁化的磁介质棒，直径为25mm，长为75mm，其总磁矩为12000A·m2．求棒的磁化强度M为多少？[解答]介质棒的面积为S=πr2，体积为V=Sl=πr2l，磁矩为pm=12000A·m2，磁化强度为=3.26×108(A·m-1)．15．2一铁环中心线的周长为30cm，横截面积为1.0cm2，在环上密绕线圈共300匝，当通有电流32mA时，通过环的磁通量为2.0×10-6Wb，求：（1）环内磁感应强度B的值和磁场强度H的值；（2）铁的磁导率μ、磁化率χm和磁化强度M．[解答]（1）根据公式B=Φ/S得磁感应强度为=0.02(T)．根据磁场的安培环路定理，由于B与dl的方向相同，得磁场强度为=32(A·m-1)．\n（2）根据公式B=μH，得铁的磁导率为=6.25×10-4(Wb·A-1·m-1)．由于μ=μrμ0，其中μ0=4π×10-7为真空磁导率，而相对磁导率为μr=1+χm，所以磁化率为．磁化强度为M=χmH=496.4×32=1.59×104(A·m-1)．15．3一螺绕环中心周长l=10cm，线圈匝数N=200匝，线圈中通有电流I=100mA．求：（1）管内磁感应强度B0和磁场强度H0为多少？（2）设管内充满相对磁导率μr=4200的铁磁质，管内的B和H是多少？（3）磁介质内部由传导电流产生的B0和由磁化电流产生的B`各是多少？[解答]（1）管内的磁场强度为=200(A·m-1)．磁感应强度为B=μ0H0=4π×10-7×200=2.5×10-4(T)．（2）当管内充满铁磁质之后，磁场强度不变H=H0=200(A·m-1)．磁感应强度为B=μH=μrμ0H=4200×4π×10-7×200=1.056(T)．（3）由传导电流产生的B0为2.5×10-4T．由于B=B0+B`，所以磁化电流产生的磁感应强度为B`=B-B0≈1.056(T)．15．4一根无限长的直圆柱形铜导线，外包一层相对磁导率为μr的圆筒形磁介质，导线半径为R1，磁介质外半径为R2，导线内有电流I通过（I均匀分布），求：（1）磁介质内、外的磁场强度H和磁感应强度B的分布，画H-r，B-r曲线说明之（r是磁场中某点到圆柱轴线的距离）；（2）磁能密度分布．[解答]（1）导线的横截面积为S0=πR12，导线内的电流密度为δ=I/S0=I/πR12．在导线内以轴线的点为圆心作一半径为r的圆，其面积为S=πr2，通过的电流为ΣI=δS=Ir2/R12．根据磁场中的安培环路定理，环路的周长为l=2πr，由于B与dl的方向相同，得磁场强度为，（0≦r≦R1）．在介质之中和介质之外同样作一半径为r的环路，其周长为l=2πr，包围的电流为I，可得磁场强度为，（r≧R1）．导线之内的磁感应强度为rrR2R1HoR1Bo；介质之内的磁感应强度为；介质之外的磁感应强度为．（2）导线之内的磁能密度为\n；介质之中的磁能密度为；介质之外的磁感应强度为．15．5一根磁棒的矫顽力为Hc=4.0×103A·m-1，把它放在每厘米上绕5匝的线圈的长螺线管中退磁，求导线中至少需通入多大的电流？[解答]螺线管能过电流I时，产生的磁感应强度为B=μ0nI．根据题意，螺线管产生的磁场强度至少要与磁棒的矫顽力大小相等，但方向相反，因此B=μ0Hc，所以电流强度为I=Hc/n=4.0×103/500=8(A)．15．6同轴电缆由两个同轴导体组成．内层是半径为R1的圆柱，外层是半径分oR1R2R3图15.6别为R2和R3的圆筒，如图所示．两导体间充满相对磁导率为μr2的均匀不导电的磁介质．设电流强度由内筒流入由外筒流出，均匀分布是横截面上，导体的相对磁导率为μr1．求H和B的分布以及im为多少？[解答]（1）导体圆柱的横截面积为S0=πR12，圆柱体内的电流密度为δ=I/S0=I/πR12．在圆柱体内以轴线的点为圆心作一半径为r的圆，其面积为S=πr2，通过的电流为ΣI=δS=Ir2/R12．根据磁场中的安培环路定理，环路的周长为l=2πr，由于B与dl的方向相同，得磁场强度为，（0≦r≦R1）．磁感应强度为，（0≦r≦R1）．（2）在介质之中同样作一半径为r的环路，其周长为l=2πr，包围的电流为I，可得磁场强度为，（R1≦r≦R2）．磁感应强度为，（R1≦r≦R2）．磁化强度为．磁化面电流的线密度为im=M×n0，n0是介质表面的法向单位矢量．在介质的两个圆形表面，由于M与n0垂直，im=|M×n0|=M．在介质的内表面，由于r=R1，所以磁化电流为．在介质的外表面，由于r=R2，所以．（3）导体圆筒的横截面积为S`=π(R32-R22)，圆筒内的电流密度为δ`=I/S`．在圆筒内以作一半径为r的圆，其面积为S=π(r2-R22)，圆所包围的电流为\n，根据安培环路定理，得磁场强度为，（R2≦r≦R3）．磁感应强度为，（R2≦r≦R3）．（4）在圆筒之外作一圆，由于包围的电流为零，所以磁场强度和磁感应强度都为零．15．7在平均半径r=0.1m，横截面积S=6×10-4m2铸钢环上，均匀密绕N=200匝线圈，当线圈内通有I1=0.63安的电流时，钢环中的磁通量Φ1=3.24×10-4Wb．当电流增大到I2=4.7安时，磁通量Φ2=6.18×10-4Wb，求两种情况下钢环的绝对磁导率．[解答]钢环中的磁感应强度为B=Φ/S；根据安培环路定理，得磁场强度为H=NI/2πr．根据公式B=μH，得绝对磁导率为．（1）在第一种情况下=2.69×10-3(H·m-1)．（2）在第二种情况下=6.88×10-4(H·m-1)．15．8一矩磁材料，如图所示．反向磁场一超过矫顽力Hc，磁化方oHM-Hc图15.8向立即翻转．用矩磁材料制造的电子计算机中存储元件的环形磁芯，其外径为0.8mm，内径为0.5mm，高为0.3mm．若磁芯原来已被磁化，方向如图所示，现在需使磁芯从内到外的磁化方向全部翻转，导线中脉冲电流I的峰值至少需要多大？设磁性材料的矫顽力Hc103(A·m-1)．[解答]直线电流I产生磁感应强度为B=μ0I/2πr，产生的磁场为H=B/μ0=I/2πr．为了磁芯从内到外的磁化方向全部翻转，电流在磁芯外侧r=0.4mm处产生的磁场应该为H=Hc，即Hc=I/2πr，所以，脉冲电流为I=2πrHc．第十六章电磁感应电磁场与电磁波16．1一条铜棒长为L=0.5m，水平放置，可绕距离A端为L/5处和棒垂直的轴OO`在水平面内旋转，每秒转动一周．铜棒置于竖直向上的匀强磁场中，如图所示，磁感应强度B=1.0×10-4T．求铜棒两端A、B的电势差，何端电势高．[解答]设想一个半径为R的金属棒绕一端做匀速圆周运动，角速度为ω，经过时间dt后转过的角度为dθ=ωdt，OO`BABL/5ω图16.1扫过的面积为dS=R2dθ/2，切割的磁通量为dΦ=BdS=BR2dθ/2，动生电动势的大小为ε=dΦ/dt=ωBR2/2．根据右手螺旋法则，圆周上端点的电势高．\nAO和BO段的动生电动势大小分别为dθLωoRl，．由于BO>AO，所以B端的电势比A端更高，A和B端的电势差为=4.71×10-4(V)．[讨论]如果棒上两点到o的距离分别为L和l，则两点间的电势差为．16．2一长直载流导线电流强度为I，铜棒AB长为L，A端与直导线的距离为xA，AB与直导线的夹角为θ，以水平速度v向右运动．求AB棒的动生oxvABIθxArldl图16.2电动势为多少，何端电势高？[解答]在棒上长为l处取一线元dl，在垂直于速度方向上的长度为dl⊥=dlcosθ；线元到直线之间的距离为r=xA+lsinθ，直线电流在线元处产生的磁感应强度为．由于B，v和dl⊥相互垂直，线元上动生电动势的大小为，棒的动生电动势为，A端的电势高．[讨论]（1）当θ→π/2时，cotθ=cosθ/sinθ→0，所以ε→0，就是说：当棒不切割磁力线时，棒中不产生电动势．（2）当θ→0时，由于，所以，这就是棒垂直割磁力线时所产生电动势．16．3如图所示，平行导轨上放置一金属杆AB，质量为m，长为L．在导轨上的端接有电阻R．匀强磁场B垂直导轨平面向里．当AB杆以BABRv0图16.3初速度v0向运动时，求：（1）AB杆能够移动的距离；（2）在移动过程中电阻R上放出的焦耳热为多少？[分析]当杆运动时会产生动生电动势，在电路中形成电流；这时杆又变成通电导体，所受的安培力与速度方向相反，所以杆将做减速运动．随着杆的速度变小，动生电动势也会变小，因而电流也会变小，所受的安培力也会变小，所以杆做加速度不断减小的减速运动，最后缓慢地停下来．[解答]（1）方法一：速度法．设杆运动时间t时的速度为v，则动生电动势为ε=BLv，电流为I=ε/R，所受的安培力的大小为F=ILB=εLB/R=(BL)2v/R，方向与速度方向相反．取速度的方向为正，根据牛顿第二定律F=ma得速度的微分方程为\n，即：积分得方程的通解为．根据初始条件，当t=0时，v=v0，可得常量C1=lnv0．方程的特解为．由于v=dx/dt，可得位移的微分方程，方程的通解为，当t=0时，x=0，所以常量为．方程的特解为．当时间t趋于无穷大时，杆运动的距离为．方法二：冲量法．由F=-(BL)2v/R，得，右边积分得，即：杆所受的冲量等于杆的动量的变化量．左边积分后，可得．（2）杆在移动过程中产生的焦耳热元为整个运动过程中产生的焦耳热为，即：焦耳热是杆的动能转化而来的．16．4如图所示，质量为m、长度为L的金属棒AB从静止开始沿倾斜的绝缘框架滑下．磁感应强度B的方向竖直向上（忽略棒AB与框架之间的摩擦），求棒AB的动生电动势．若棒AB沿光滑的金属框架滑下，设金属棒与金属框组成的回路的电阻R为常量，棒AB的动生电动势又为ABθCDB图16.4多少？[解答]（1）棒的加速度为a=gsinθ，经过时间t，棒的速度为v=at=(gsinθ)t，而切割磁力线的速度为v⊥=vcosθ，所以棒的动生电动势为ε=BLv⊥=BLg(sinθcosθ)t=BLg(sin2θ)t/2．（2）设棒运动时间t时的速度为v，则动生电动势为ε=BLvcosθ，电流为I=ε/R，所受的安培力的大小为F=ILB=εLB/R=(BL)2vcosθ/R，\n其方向水平向右．安培力沿着斜面向上的分量为F`=Fcosθ，其方向与速度的方向相反．取速度的方向为正，根据牛顿第二定律ΣF=ma得速度的微分方程为，即，方程可化为．积分得方程的通解为．根据初始条件，当t=0时，v=0，可得常量，方程的特解为，棒的速度为，动生电动势为．[讨论]当时间t趋于无穷大时，最终速度为，最终电动势为，最终电流为．另外，棒最终做匀速运动，重力做功的功率等于感生电流做功的功率，重力做功的功率为P=mgsinθv，感生电流做功的功率为，两式联立也可得，由此可以求出最终电动势和电流．[注意]只有当物体做匀速运动时，重力所做的功才等于电流所做的功，否则，重力还有一部分功转换成物体的动能．16．5电磁涡流制动器是一个电导率为σ，厚度为t的圆盘，此盘绕通过其中心的垂直轴旋转，且有一覆盖小面积为a2的均匀磁场B垂直于圆盘，小面积离轴r（r>>a）．当圆盘角速度为ω时，试证此圆盘受到一阻碍其转动的磁力矩，其大小raa图16.5Bωt近似地表达为M≈B2a2r2ωσt．[解答]电导率是电阻率的倒数σ=1/ρ．不妨将圆盘与磁场相对的部分当成长、宽和高分别为a、a和t的小导体，其横截面积为S=at，电流将从横截面中流过，长度为a，因此其电阻为\naatSI．宽为a的边扫过磁场中，速度大小为v=rω，产生的感生电动势为ε=Bav=Barω，圆盘其他部分的电阻远小于小导体的电阻，因此通过小导体的电流强度为I=ε/R=Barωσt，所受的安培力为F=IaB=B2a2rωσt，其方向与速度方向相反．产生的磁力矩为M=Fr=B2a2r2ωσt．其方向与角速度的方向相反．16．6如图，有一弯成θ角的金属架COD放在磁场中，磁感应强度B的方向垂直于金属架COD所在平面，一导体杆MN垂直于OD边，并在金属架上以恒定速度v向右滑动，v与MN垂直，设t=0时，x=0，求下列两情形，框架内的感应电动势εi．BMNOvCDxθ图16.6（1）磁场分布均匀，且B不随时间改变；（2）非均匀的交变磁场B=Kxcosωt．[解答]（1）经过时间t，导体杆前进的距离为x=vt，杆的有效长度为l=xtanθ=v(tanθ)t，动生电动势为εi=Blv=Bv2(tanθ)t．（2）导体杆扫过的三角形的面积为S=xl/2=x2tanθ/2=v2t2tanθ/2，通过该面的磁通量为感应电动势为，即：．16．7如图所示的回路，磁感应强度B垂直于回路平面向里，磁通量按下述规律变化Φ=3t2+2t+1，式中Φ的单位为毫韦伯，t的单位为秒．求：BR图16.7（1）在t=2s时回路中的感生电动势为多少？（2）电阻上的电流方向如何？[解答]（1）将磁通量的单位化为韦伯得Φ=(3t2+2t+1)/103，感生电动势大小为ε=|dΦ/dt|=2(3t+1)/103．t=2s时的感生电动势为1.4×10-2(V)．（2）由于原磁场在增加，根据楞次定律，感应电流所产生的磁场的方向与原磁场的方向相反，所以在线圈中感生电流的方向是逆时针的，从电阻的左边流向右边．16．8如图所示的两个同轴圆形导体线圈，小线圈在大线圈上面．两线圈的距离为x，设x远大于圆半径R．大线圈中通有电流I时，若半径为r的小线圈中的磁场可看作是均匀的，且以速率v=dx/dt运动．求x=NR时，小线圈中的感应电动势为多xrIoRB图16.8少？感应电流的方向如何？[解答]环电流在轴线上产生的磁感应强度为，当x>>R时，磁感应强度为．小线圈的面积为S=πr2，通过的磁通量为\n，当小线圈运动时，感应电动势为，当x=NR时，感应电动势为．感应电流的磁场与原磁场的方向相同，感应电流的方向与原电流的环绕方向相同．16．9如图所示，匀强磁场B与矩形导线回路的法线n成θ=60°角，B=kt（k为大于零的常数）．长BAθLDBnv图16.9为L的导体杆AB以匀速v向右平动，求回路中t时刻的感应电动势的大小和方向（设t=0时，x=0）．[解答]经过时间t，导体杆运动的距离为x=vt，扫过的面积为S=Lx=Lvt，通过此面积的磁通量为Φ=B·S=BScosθ=Lvkt2/2．感应电动势的大小为ε=dΦ/dt=Lvkt．由于回路中磁通量在增加，而感应电流的磁通量阻碍原磁通量增加，其磁场与原磁场的方向相反，所以感应电动势的方向是顺时针的．16．10长为b，宽为a的矩形线圈ABCD与无限长直截流导线共面，且线圈的长边平行于长直导线，线圈以速度v向右平动，t时刻基AD边距离长直导线为x；且长直导线中的电流按I=I0cosωt规律随时BABvDCxrxdrxbxa图16.10间变化，如图所示．求回路中的电动势ε．[解答]电流I在r处产生的磁感应强度为，穿过面积元dS=bdr的磁通量为，穿过矩形线圈ABCD的磁通量为，回路中的电动势为．显然，第一项是由于磁场变化产生的感生电动势，第二项是由于线圈运动产生的动生电动势．*16．11如图，一个矩形的金属线框，边长分别为a和b（b足够长）．金属线框的质量为m，自感系数为L，忽略电阻．线框的长边与x轴平行，它以速度v0沿x轴的方向从磁场外进入磁感应强度为B0的均匀磁场中，B0的方向垂直矩形线框平面．求矩形线框在磁场中速度与时间的关系式v=v(t)和沿x轴方向移动的距离与时间的关系式xB0v0bxaxoxy图16.11=x(t)．[解答]由于b边很长，所以线框只有右边在做切割磁力线的运动．当线框速度为v时，产生的动生电动势为ε=B0av．当线框中的电流为i时，产生的自感电动势的大小为．根据欧姆定律得ε+εL=iR，由于不计电阻，所以有．①右边所受的力为F=iaB0，根据牛顿第二定律得，\n微分得，②联立①和②式得微分方程，这是简谐振动的微分方程，其通解为．当t=0时，v=v0，所以A=v0．加速度at=dv/dt，当t=0时，at=0，所以B=0．速度方程为．由于v=dx/dt，所以．当t=0时，x=0，所以C=0，所以位移方程为．BabRcrr图16.1216．12如图所示的圆面积内，匀强磁场B的方向垂直于圆面积向里，圆半径R=12cm，dB/dt=10-2T·s-1．求图中a、b、c三点的涡旋电场为多少（b为圆心）？设ab=10cm，bc=15cm．[解答]（1）当点在磁场之中时，以b为圆心，以r为半径作一圆形环中，其周长为C=2πr，面积为S=πr2．取环路的逆时针方向为正，根据右手螺旋法则，面积的法向方向垂直纸面向外。根据安培环路定理，由于磁场增加，其变化率的方向与磁场方向相同，而感应电流的磁场与磁场增加的方向的方向相反，即垂直纸面向里，根据右手螺旋法则，涡旋电场的方向与环路方向相同，所以左边等于．而磁感应强度的方向与面积的法向方向相反，所以右边等于．因此涡旋电场为．对于a点，由于r=0.1m，所以Ek=0.1×0.01/2=5×10-4(V·m-1)．对于b点，由于r=0，所以Ek=0．（2）当点在磁场之外时，以b为圆心，以r为半径作一圆形环路．根据安培环路定理，左边的积分仍然为Ek2πr．由于半径R之外的磁感应强度及其变化率为零，所以右边的大小为πR2dB/dt，因此涡旋电场为．对于c点，由于r=0.15m，R=0.12m，所以Ek=(0.12)2×0.01/2×0.15=4.8×10-4(V·m-1）．16．13两个共轴的导体圆筒称为电缆，其内、外半径分别为r1和r2，设电流由内筒流入，外筒流出，求长为l的一段电缆的自感系数（提示：按定义L=NΦ/I，本题中Ir1olr2I图16.13NΦ是图中阴影部分面积的磁通量）．[解答]在内外半径之间，磁感应强度的大小为B=μ0I/2πr，\n其中r是场点到轴线之间的距离，B的方向是以轴线为中心的同心圆．在r处取一长为l的面积元dS=ldr，通过面积元的磁通量为dΦ=BdS，总磁通量为，电缆的自感系数为．[讨论]电缆单位长度的自感系数为．16．14两个共轴圆线圈，半径分别为R和r，匝数分别为N1和N2，两者相距L．设小线圈的半径很小，小线圈处的磁场近似地可视为均匀，求两线圈的互感系数．[解答]设大线圈中通以电流I1，N1匝线圈形成的环电流在轴线上产生的磁感应强度为LrI1oRB图16.14，小线圈的面积为S=πr2，大线圈通过一匝小线圈的磁通量为，在小线圈中产生的全磁通为，互感系数为．[讨论]当两线圈相距很远时，L>>R，互感系数约为．16．15两个共轴的长直螺线管长为L，半径分别为R1和R2，设R2>R1；匝数分别为N1和N2．求两螺线管的互感系数．[解答]设大螺线管中通以电流I2，在轴线上产生的磁感应强度为B=μ0n2I2=μ0N2I2/L．小螺线管的面积为S=πR12，大螺线圈通过一匝小螺线管的磁通量为Φ=BS=πμ0N2I2R12/L，在小线圈中产生的全磁通为Φ12=N1Φ=πμ0N1N2I2R12/L，互感系数为M=Φ12/I2=πμ0N1N2R12/L．16．16一圆形线圈C1由50匝表面绝缘的细导线密绕而成，圆面积S=2cm2，将C1放在一个半径RI2C2C1图16.16=20cm的大圆线圈C2的中心，两线圈共轴，C2线圈为100匝．求：（1）两线圈的互感M；（2）C2线圈中的电流以50A·s-1的速率减少时，C1中的感应电动势为多少？[解答](1)设大线圈中通以电流I2，N2匝线圈形成的环电流在圆心产生的磁感应强度为B=μ0N2I2/2R，小线圈中的全磁通为Φ12=N1BS=μ0N1N2I2S/2R，互感系数为M=Φ12/I2=μ0N1N2S/2R=4π×10-7×50×100×2×10-4/2×0.2=10-6π(H)．(2)C1中的感应电动势的大小为ε=MdI2/dt=10-6π×50=5×10-5π(V)．16．17长直导线与矩形单匝线圈共面放置，导线与线圈的长边平行，矩形线圈的边长分别为a、b，它到直导线的距离为c（如图），当矩形线圈中通有电流I=I0sinωt时，Ibca图16.17求直导线中的感应电动势．[解答]如果在直导线中通以稳恒电流I，在距离为r处产生的磁感应强度为B=μ0I/2πr．在矩形线圈中取一面积元dS=bdr，通过线圈的磁通量为\n，互感系数为．当线圈中通以交变电流I=I0sinωt时，直导线中的感应电动势大小为．16．18在长圆柱形的纸筒上绕有两个线圈1和2，每个线圈的自感都是0.01H，如图所示．求：（1）线圈1的a端和线圈2的a`端相接时，b和b`之间的自感L为abb`a`图16.18多少？（2）线圈1的b端和线圈2的a`端相接时，a和b`之间的自感L为多少？[解答]（1）当线圈1的a端和线圈2的a`端相接时，在b和b`之间通以电流I，两个线圈产生的磁场方向相反，由于两个线圈是相同的，总磁场B=0，所以磁场能量为零，自感L也为零．（2）当线圈1的b端和线圈2的a`端相接时，在a和b`之间通以电流I，两个线圈产生的磁场方向相同，由于两个线圈是相同的，总磁场为B=B1+B2=2B1，磁场的能量为12341234ab图16.19．自感系数为=0.04(H)．16．19两个线圈的自感分别为L1和L2，，它们之间的互感为M．将两个线圈顺串联，如图a所示，求1和4之间的互感；（2）将两线圈反串联，如图b所示，求1和3之间的自感．[解答]两个线圈串联时，通以电流I之后，总磁场等于两个线圈分别产生的磁场的矢量和B=B1+B2，磁场的能量为．（1）当两个线圈顺串时，两磁场的方向相同，θ=0，所以，自感系数为．（2）当两个线圈反串时，两磁场的方向相反，θ=π，所以，自感系数为．16．20两个共轴的螺线管A和B完全耦合，A管的自感系数L1=4.0×10-3H，通有电流I1=2A，B管的自感L2=9×10-3H，通有电流I2=4A．求两线圈内储存的总磁能．[解答]A管储存的自能为，\nB管储存的自能为；由于两线圈完全耦合，互感系数为，A管和B管储存的相互作用能为Wm12=MI1I2=6×10-3×2×4=48×10-3(J)，两线圈储存的总能量为Wm=Wm1+Wm2+Wm12=0.128(J)．16．21一螺绕环中心轴线的周长L=500mm，横截面为正方形，其边长为bboo`bI图16.21=15mm，由N=2500匝的绝缘导线均匀密绕面成，铁芯的相对磁导率μr=1000，当导线中通有电流I=2.0A时，求：（1）环内中心轴线上处的磁能密度；（2）螺绕环的总磁能．[解答]（1）设螺绕环单位长度上的线圈匝数为n=N/L，中心的磁感应强度为B=μnI，其中μ=μrμ0．磁场强度为H=B/μ=nI，因此中心轴线上能量密度为=2π×104(J·m-3)．（2）螺绕环的总体积约为V=b2L，将磁场当作匀强磁场，总磁能为W=wV=2π×104×(0.015)2×0.5=2.25π=7.07(J)．16．22试证：平行板电容器中的位移电流可写成的形式，式中C是电容器的电容，U是两板间的电势差．对于其他的电容器上式可以应用吗？[证明]根据麦克斯韦理论：通过电场任意截面的位移电流强度等于通过该截面电位移通量的时间变化率，即Id=dΦD/dt．在平行板电容器中，由于ΦD=DS，而电位移D等于电容器的面电荷密度，即D=σ．因为电容器带电量为q=σS=DS=ΦD，所以Id=dq/dt，即：位移电流等于极板上电量的时间变化率．根据电容的定义C=q/U，可得Id=CdU/dt．其他电容器可以看作由很多平等板电容器并联而成，总电容等于各电容之和，所以此式对于其他电容器也可以应用．16．23如果要在一个1.0PF的电容器中产生1.0A的位移电流，加上电容器上的电压变化率为多少？[解答]因为Id=CdU/dt，所以电压变化率为dU/dt=Id/C=1/10-12=1012(V·s-1)．16．24在圆形极板的平行板电容器上，加上频率为50Hz，峰值为2×105V的交变电压，电容器电容C=2PF，求极板间位移电流的最大值为多少？[解答]交变电压为U=Umcos2πνt，位移电流为Id=CdU/dt=-CUm2πνsin2πνt，电流最大值为Im=CUm2πν=2×10-12×2×105×2π×50=4π×10-5(A)．16．25一平行板电容器的两极板面积为S的圆形金属板，接在交流电源上，板上电荷随时间变化，q=qmsinωt．求：（1）电容器中的位移电流密度；（2）两极板间磁感应强度的分布．\n[解答](1)平行板电容器的面电荷密度为σ=q/S，位移电流密度为．（2）在安培-麦克斯韦环路定律中，两极板间没有传导电流，即I=0．由于轴对称，在两板之间以轴为圆心作一个半径为r的圆，其周长为C=2πr，使磁场的方向与环路的方向相同，左边为．环路所包围的面积为S`=πr2，右边的位移电流为．因此，两极板间磁场强度的分布为，磁感应强度的分布为．16．26如图所示，电荷+q以速度v向O点运动（电荷到O点的距离以x表示）．以O点O圆心作一半径为a的圆，圆面与v垂直．试计算通过此圆面的位移电流．a[解答]在圆面上取一半径为R的环，其面积为dS=2πRdR，环上任一面元的法线方向与场强方向之间的夹角为φ，场强大小为E=q/4πε0r2，其中r=(x2+R2)1/2，通过环的电通量为Oqravxθ图16.26dΦe=E·dS=EdScosφ，其中cosφ=x/r，所以得，积分得电通量为．由于电位移强度D和电场强度E的关系为D=ε0E，所以电位移通量和电通量之间的关系为Φd=ε0Φe，OqrvxθrREφ因此点电荷在圆面上通过的电位移通量为．当电荷q以速度v向O运动时，可认为圆面以dx/dt=-v向电荷运动，因此，通过此圆面的位移电流为．16．27在真空中，一平面电磁波的电场为(V·m-1)．求：（1）电磁波的波长和频率；（2）传播方向；（3）磁场的大小和方向．[解答]（1）电磁波的角频率为ω=2π×107(rad·s-1)，频率为ν=ω/2π=107(Hz)．波长为λ=cT=c/ν=3×108/107=30(m)．（2）电磁波的传播方向为x方向．（3）磁场的方向在z方向，由于，所以磁场强度为\n．磁感应强度为．16．28一个长直螺线管，每单位长度有n匝线圈，载有电流i，设i随时间增加，di/dt>0，设螺线管横截面为圆形，求：oirEBSidl（1）在螺线管内距轴线为r处某点的涡旋电场；（2）在该点处坡印廷矢量的大小和方向．[解答]（1）长直螺线管通有电流i时，在轴线上产生的磁感应强度为B=μ0ni，磁场是均匀的，也是轴对称的．以轴线上某点为圆心，以r为半径作一环路，环路的周长为C=2πr，面积为S=πr2，根据电场的环路定理，可得2πrE=-πr2dB/dt，因此涡旋电场为，负号表示涡旋电场的方向与环路的环绕方向相反．（2）管中磁场强度为H=B/μ0=ni．坡印廷矢量为S=E×H，其大小为．当di/dt>0时，S的方向沿径向指向轴线；当di/dt<0时，S的方向沿径向向外．16．29有一氦氖激光管所发射的激光功率为10×10-3W，设激光为圆柱形光束，圆柱横截面直径为2.0×10-3m，试求激光的最大电场强度和最大磁感应强度为多少？[解答]圆柱面积为S=πr2，坡印廷矢量的平均值为．设最大电场强度为E0和最大磁感应强度为B0，可以证明：．由于，可得，所以(V·m-1），[取ε0=1/4πk=1/(4π×9×109)]．同理，，磁感应强度的最大值为(T)，（取μ0=4π×10-7）．16．30一平行板电容器由相距为L的两个半径为a的圆形导体板构成，略去边缘效应．证明：在电aEHSS`S``L容器充电时，流入电容器的能量速率等于其静电能增加的速率．[证明]电容器的面积为S`=πa2，电容器充了电量q时，面电荷密度为σ=q/S`，不计边缘效应，边缘的场强为E=σ/ε0=q/S`ε0．在边缘做一个半径为a的环路，其周长为2πa，面积为S`．根据环路定理，\n左边为2πaH；右边的I=0，Id=dq/dt，所以磁场强度为．()坡印廷矢量为S=E×H，其大小为，方向垂直环路指向轴线．电容器侧面的表面积为S``=2πaL，流入电容器的能量速率为．当电容器带电q时，根据电容公式C=q/U，两端的电压为U=q/C，所带的静电能为，静电能的增加速率为．SII图16.31SSSSSSSSSSS由于电容，所以，流入电容器的能量速率等于其静电能增加的速率．16．31半径为a的长直导体载有沿轴线方向的电流I，I均匀地分布在横截面上．证明：（1）在导线表面，坡印廷矢量S的方向垂直于导线表面向内；（2）导体内消耗的焦耳热等于S传递来的能量．[证明]（1）导体的横截面积为S`=πa2，aEHSIIaS`S```L电流密度为δ=I/S`．导体的电阻率为ρ，电场强度大小为E=ρδ，方向与电流的流向相同．在导体表面做一个半径为a的环路，其周长为C=2πa．根据环路定理，左边为2πaH；右边的Id=0，所以磁场强度为H=I/2πa．由于电场强度E的方向沿着轴向，磁场强度方向沿着环路，根据S=E×H，可知：在导线表面，坡印廷矢量S的方向垂直于导线表面向内．（2）在导体表面的坡印廷矢量的大小为，对于长为L的导体来说，其表面积为S``=2πaL，单位时间内传递来的能量为，其中正好是这段导体的电阻，而I2R是导体消耗焦耳热的功率，所以导体内消耗的焦耳热等于S传递来的能量．16．32如图所示的电路，在电键K接通后，电池中的稳恒电流为10A，（线L=2H,R=0εC=8μFRK图16.32圈的电阻R=0）．（1）说明为什么当电键断开时，L-C电路就发生振荡电流；（2）求振荡电流的频率；（3）求电容器两端的最大电势差；（4）若线圈的电阻R≠0，试讨论能否发生振荡？如能振荡，振荡频率为多少？[解答]（1）当电键K接通后，由于电池中的电流是稳恒的，电流不通过电容器，只通过电感L．K断开时，L中的电流发生了变化，就会产生感应生动势，给电容器C充电；电容器充完电之后又放电．这个过程不断进行，就产生振荡电流．（2）振荡电流的频率为\n=37.79(Hz)．（3）电量的方程为q=qmcosωt，电流的方程为I=dq/dt=-ωqmsinωt，其中ωqm=im，所以最大电量为qm=im/ω．电容器两端的最大电势差为(V)．（4）当线圈中电阻不为零时，电流通过电阻要产生电压降iR，当电容器带电时，两端的电压为Uc=q/C；当电感中电流变化时，产生的感应电动势大小为UL=Ldi/dt．它们相当于两个电源，方向相同，而与电阻上电压降的方向相反，所以电路方程为．由于I=dq/dt，所以方程变为．设方程的解为q=Aert，代入微分方程可得Lr2+Rr+1/C=0．根的判别式为D=R2-4L/C，当R2≧4L/C时，ert只有实部，电路不能发生振荡．当R2<4L/C时，设r=α+ωi(i为虚数单位)，其中，．电路能够发生振荡，振荡频率为．α使振幅按指数规律减小．[讨论]当电路中的电阻R=0时，α=0，频率为，这正是纯LC电路的振荡频率．16．33一飞机在离电台10km处飞行，收到电台的讯号强度为10×10-6W·m-2，求：（1）该电台发射的讯号在飞机所在处的电场强度的峰值E0和磁场强度的峰值H0为多少？（2）设电台发射是各向同性的，求电台的发射功率．[解答]（1）飞机电台收到讯号强度就是平均坡印廷矢量，根据16．29题的结果得电场强度的峰值为=8.68×10-2(V·m-1)，磁场强度的峰值为=2.3×10-4(A·m-1)．（2）电台的发射功率等于单位时间内通过飞机所在球面的平均能量，即=4π×(104)2×10×10-6=4π×103(W)=12.56(kW)．第十七章量子物理基础17．1根据玻尔理论，计算氢原子在n=5的轨道上的动量矩与其在第一激发态轨道上的动量矩之比．[解答]玻尔的轨道角动量量子化假设认为电子绕核动转的轨道角动量为，对于第一激发态，n=2，所以L5/L2=5/2．\n17．2设有原子核外的3p态电子，试列出其可能性的四个量子数．[解答]对于3p态电子，主量子数为n=3，角量子数为l=1，磁量子数为ml=-l,-(l-1),…,l-1,l，自旋量子数为ms=±1/2．3p态电子的四个可能的量子数(n,l,ml,ms)为(3,1,1,1/2)，(3,1,1,-1/2)，(3,1,0,1/2)，(3,1,0,-1/2)，(3,1,-1,1/2)，(3,1,-1,-1/2)．17．3实验表明，黑体辐射实验曲线的峰值波长λm和黑体温度的乘积为一常数，即λmT=b=2.897×10-3m·K．实验测得太阳辐射波谱的峰值波长λm=510nm，设太阳可近似看作黑体，试估算太阳表面的温度．[解答]太阳表面的温度大约为=5680(K)．17．4实验表明，黑体辐射曲线和水平坐标轴所围成的面积M（即单位时间内从黑体单位表面上辐射出去的电磁波总能量，称总辐射度）与温度的4次方成正比，即M=σT4，其中σ=5.67×10-8W·m-2·K-4．试由此估算太阳单位表面积的辐射功率（太阳表面温度可参见上题）．[解答]太阳单位表面积的辐射功率大约为M=5.67×10-8×(5680)4=5.9×107(W·m-2)．17．5宇宙大爆炸遗留在宇宙空间的均匀背景辐射相当于3K黑体辐射．求：（1）此辐射的单色辐射强度在什么波长下有极大值？（2）地球表面接收此辐射的功率是多少？[解答]（1）根据公式λmT=b，可得辐射的极值波长为λm=b/T=2.897×10-3/3=9.66×10-4(m)．（2）地球的半径约为R=6.371×106m，表面积为S=4πR2．根据公式：黑体表面在单位时间，单位面积上辐射的能量为M=σT4，因此地球表面接收此辐射的功率是P=MS=5.67×10-8×34×4π(6.371×106)2=2.34×109(W)．17．6铝表面电子的逸出功为6.72×10-19J，今有波长为λ=2.0×10-7m的光投射到铝表面上．试求：（1）由此产生的光电子的最大初动能；（2）遏止电势差；（3）铝的红限波长．[解答]（1）光子的能量为E=hν=hc/λ，根据爱因斯坦光电效应方程hν=Ek+A，产生的光电子的最大初动能为Ek=hν-A=6.63×10-34×3×108/2.0×10-7-6.72×10-19=3.23×10-19(J)．（2）遏止电势差的公式为eUs=Ek，遏止电势差为Us=Ek/e=3.23×10-19/1.6×10-19=2.0(V)．（3）铝的红限频率为ν0=A/h，红限波长为λ0=c/ν0=hc/A=6.63×10-34×3×108/6.72×10-19=2.96×10-7(m)．17．7康普顿散射中入射X射线的波长是λ=0.70×10-10m，散射的X射线与入射的X射线垂直．求：（1）反冲电子的动能EK；（2）散射X射线的波长；（3）反冲电子的运动方向与入射X射线间的夹角θ．h/λ`ph/λθ[解答]（1）（2）根据康普顿散射公式得波长变化为=2.426×10-12(m)，散射线的波长为λ`=λ+Δλ=0.72426×10-10(m)．反冲电子的动能为=9.52×10-17(J)．\n（3）由于，所以夹角为θ=44°1`．17．8求波长分别为λ1=7.0×10-7m的红光；λ2=0.25×10-10m的X射线的能量、动量和质量．[解答]X射线的能量为E=hν=hc/λ，动量为p=h/λ；由E=hc/λ=mc2，得其质量为m=h/cλ．对于红光来说，能量为=2.84×10-19(J)，动量为=9.47×10-25(kg·m·s-1)，质量为=3.16×10-36(kg)．对于X射线来说，能量为=7.956×10-15(J)，动量为=2.652×10-23(kg·m·s-1)，质量为=8.84×10-32(kg)．17．9处于第四激发态上的大量氢原子，最多可发射几个线系，共几条谱线？那一条波长最长．[解答]第四激发态的氢原子处于第5个能级，最多可发射四个线系．（1）能级5到4，1条谱线；（2）能级5和4到3，2条谱线；（3）能级5、4和3到2，3条谱线；（3）能级5、4、3和2到1，4条谱线．共10条谱线．从能级5跃迁到4发射的光谱频率最小，波长最长．17．10设氢原子中电子从n=2的状态被电离出去，需要多少能量．[解答]氢原子能级公式为，当n=1时，基态能级的能量为≈-2.18×10-18(J)=-13.6(eV)，因此．当电子从n能级跃迁到m能级时放出（正）或吸收（负）光子的能量为．电离时，m趋于无穷大．当电子从n=2的能级电离时要吸收能量=-3.4(eV)，因此需要3.4eV的能量．17．11质量为m的卫星，在半径为r的轨道上环绕地球运动，线速度为v．（1）假定玻尔氢原子理论中关于轨道角动量的条件对于地球卫星同样成立．证明地球卫星的轨道半径与量子数的平方成正比，即r=Kn2，（式中K是比例常数）；（2）应用（1）的结果求卫星轨道和下一个“容许”轨道间的距离，由此进一步说明在宏观问题中轨道半径实验上可认为是连续变化的（利用以下数据作估算：普朗克常数h=6.63×10-34J·s，地球质量M=\n6×1024kg，地球半径R=6.4×103km，万有引力常数G=6.7×10-11N·m2·kg-2．[解答]（1）卫星绕地球运动的向心力是万有引力；根据玻尔理论，角动量为mvr=nh/2π．将前式乘以mr3得，所以，即：卫星的轨道半径与量子数的平方成正比．（2）假设卫星质量m=100kg，比例系数为=2.77×10-87．可见：比例系数很小．当r=R时，地球表面的量子数为．可见：地球表面处的量子数很大．地面以上的量子数设为n`，(n`=1,2,3,…)，则总量子数可表示为两个量子数之和：n=n0+n`．轨道间的距离为Δr=K[(n0+n`+1)2-(n0+n`)2]=K[2(n0+n`)+1]．由于n0>>1，所以Δr=2Kn0+2Kn`．设n`=kn0，即：取地面以上的量子数为地球表面量子数的倍数，有n=(k+1)n0，则r=Kn02(k+1)2，Δr=2Kn0(k+1)=2.66×10-40(k+1)．这说明：当地面以上的量子数按k+1成倍地增加时，半径将按k+1的平方的规律增加，而轨道之间的距离只按k+1的一次方的规律增加；由于Δr的系数很小，所以轨道间距是非常非常小的，因此可认为轨道半径是连续变化的．17．12电子和光子各具有波长2.0×10-10m，它们的动量和总能量各是多少？[解答]它们的动量都为=3.315×10-24(kg·m·s-1)．根据公式E2=p2c2+m02c4，电子的总能量为=3×108×[(3.315×10-24)2+(9.1×10-31×3×108)2]1/2=8.19×10-14(J)．光子的静止质量为零，总能量为E=cp=3×108×3.315×10-24=9.945×10-16(J)．17．13室温下的中子称为热中子T=300K，试计算热中子的平均德布罗意波长．[解答]中子热运动的平均速度为其中k为玻尔兹曼常数k=1.38×10-23J·K-1，mp是电子的质量mp=1.675×10-27kg，可得平均速度为=2.509×104(m·s-1)，平均动量为=4.2×10-27(kg·m·s-1)．平均德布罗意波长为=1.58×10-10(m)=0.158(nm)．17．14一束动量是p的电子，通过缝宽为a的狭缝，在距离狭缝为R处放置一屏，屏上电子衍射图样中央最大的宽度是多少？[解答]根据动量和位置的不确定关系Δpx·Δx≧h，其中位置不确定量为Δx=a，动量的不确定量为Δpx=psinθ．设电子衍射图样的中央最大半宽度为w，则sinθ=w/R，\n可得，宽度为．[注意]如果将h改为ћ/2，则宽度为2w≧ћR/pa．两者相差很小．17．15一宽度为a的一维无限深势阱，试用不确定关系估算阱中质量为m的粒子最低能量为多少？[解答]粒子坐标的不确定范围是Δx≦a，动量的不确定范围是Δp≧h/Δx≧h/a．这也就是动量p的范围．因此能量为E=p2/2m≧h2/2ma2，最低能量可估计为Emin=h2/2ma2．17．16设有一宽度为a的一维无限深势阱，粒子处于第一激发态，求在x=0至x=a/3之间找到粒子的几率？[解答]粒子在一维无限深势阱中的定态波函数为，Ψ(x)=0，(x<0，x>a)．当粒子处于第一激发态时，n=2，在x=0至x=a/3之间被发现的几率为=0.391．17．17设粒子在宽度为a的一维无限深势阱运动时，其德布罗意波在阱内形成驻波，试利用这一关系导出粒子在阱中的能量计算式．[解答]当粒子在势阱中形成稳定驻波时，势阱宽度必然为半波长的整数倍，即n(λ/2)=a，(n=1,2,3,…)．根据德布罗意假设λ=h/p，可得粒子的动量为能量为．17．18假定对某个粒子动量的测定可精确到千分之一，试确定这个粒子位置的最小不确定量．（1）该粒子质量为5×10-3kg，以2m·s-1的速度运动；（2）该粒子是速度为1.8×108m·s-1的电子．[解答]粒子的动量为p=mv，动量的不确定量为Δp=p/1000，根据动量和位置的不确定关系Δp·Δx≧ћ/2，位置的不确定量为Δx=ћ/2Δp．（1）=5.276×10-30(m)．（2）=3.22×10-10(m)．17．19设有某线性谐振子处于第一激发态，其波函数为．式中，k为常数，则该谐振子在何处出现的概率最大？\n[解答]第一激发态的概率为，对x求导得，令dw/dt=0，得概率最大的位置为x=±1/a．17．20一维运动的粒子，处于如下的波函数所描述的状态式中λ>0，A为常数．（1）将此波函数归一化；（2）求粒子位置的概率分布函数；（3）粒子在在何处出现的概率最大？[解答]（1）归一化得，所以A=2λ3/2．归一化波函数为（[注]利用Γ函数的性质可简化积分过程．，当n为整数时，Γ(n)=(n-1)!．设y=2λx，则dx=dy/2λ，可得，可以得出同一结果．）（2）粒子坐标的几率分布函数为（3）利用上一题的方法求导可得几率最大的位置为x=1/λ．17．21设有某一维势场如下：该势场可称为有限高势阱，设粒子能量EL)．（6）当x→-∞时，ψ1有限，所以B1=0；当x→∞时，ψ3有限，所以A3=0．当x=0时，ψ1(0)=ψ2(0)，可得A1=A2；（7）同时ψ1`(0)=ψ2`(0)，可得k1A1=k2B2．（8）当x=L时，ψ2(L)=ψ3(L)，ψ2`(L)=ψ3`(L)，可得A2cosk2L+B2sink2L=B3exp(-k1L)；（9）-k2A2sink2L+k2B2cosk2L=-k1B3exp(-k1L)(10)将（9）乘以k1加（10）得k1A2cosk2L+k1B2sink2L-k2A2sink2L+k2B2cosk2L=0．即(k1A2+k2B2)cosk2L=(k2A2-k1B2)sink2L，亦．（11）由（7）和（8）得k1A2=k2B2，即B2=k1A2/k2，（12）（12）代入（11）式得，即．（13）这就是总能量满足的关系式．17．22原子内电子的量子态由n、l、ml、ms四个量子数表征，当n、l、ml一定时，不同的量子态数目为多少？当n、l一定时，不同量子态数目为多少？当n一定时，不同量子态数目为多少？[解答]当n、l、ml一定时，ms只取两个值，所以量子态数目为2．当n、l一定时，ml有(2l+1)种不同取值，所以量子态数目为2(2l+1)．当n一定时，l从0到(n-1)共有n种不同取值，量子态数目为\n．