大学物理精细讲解课件

大学物理精细讲解课件

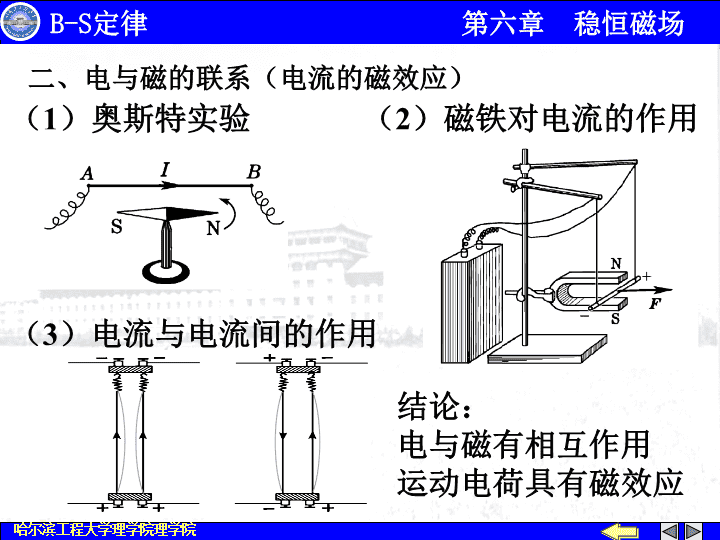
法国物理学家，电动力学的创始人。少年时期主要跟随父亲学习技艺，没有受过正规系统的教育。安培自幼聪慧过人，对事物有敏锐的观察力。他兴趣广泛，爱好多方面的科学知识。1799年安培开始系统研究数学，1805年定居巴黎，担任法兰西学院的物理教授，1814年参加了法国科学会，1818年担任巴黎大学总督学，1827年被选为英国皇家学会会员。他还是柏林科学院和斯德哥尔摩科学院院士。安培是近代物理学史上功绩显赫的科学家。特别在电磁学方面的贡献尤为卓著。从1814年参加科学会开始，在以后的二十多年中，他发现了一系列的重要定律、定理，推动了电磁学的迅速发展。1827年他首先推导出了电动力学的基本公式，建立了电动力学的基本理论，成为电动力学的创始人。安培善于深入研究他所发现的各种规律，并且善于应用数学进行定量分析。1822年在科学学会上，他正式公布了他发现的安培环路定理。在电动力学中，这是一个重要的基本定律之一。安培的研究工作结束了磁是一种特殊物质的观点，使电磁学开始走上了全面发展的道路。为了纪念他的贡献，以他的名字命名了电流的单位。安培(Andre-MarieAmpere,1775-1836)\n6.1基本磁现象一、磁铁的性质：（1）磁极：磁铁中磁性较强的区域。中性区：无磁性的区域。磁极的分类：南(S)极、北(N)极。（2）磁力：磁铁之间的作用力。“同性相斥，异性相吸”。（3）自然界中不存在单独的N、S极。第六章稳恒磁场\n二、电与磁的联系（电流的磁效应）结论：电与磁有相互作用运动电荷具有磁效应（1）奥斯特实验（2）磁铁对电流的作用（3）电流与电流间的作用\n\n三、安培假说假说：一切磁现象都起源于电流。在磁性物质分子中，存在着回路电流，称分子电流，它相当于一个基元磁铁。若将这些分子电流定向地排列起来，宏观上显示出N、S极来。分子电流\n6.2磁场磁感应强度一、磁场任何运动电荷或电流，在其周围空间均产生磁场特点:（1）矢量场，既有大小，又有方向。（2）对磁场中的运动电荷或电流有力的作用。（3）载流导体在磁场中运动时，磁力对其作功。在引入磁场概念后，所有的磁相互作用都是通过磁场来进行传递的。运动电荷运动电荷磁场\n二、磁感应强度（通过磁场对载流线圈的作用引入）磁矩：磁矩是一个描述平面载流线圈自身性质的物理量。在磁场中引入实验线圈：（1）几何尺寸很小；（2）I很小。InΔS\n2.由平衡位置转900，此时线圈所受力矩最大，且对给定点来说MmaxPm，而Mmax/Pm仅与线圈所在位置有关、与线圈无关，反映了磁场自身的性质。定义大小：方向：平衡位置处Pm的方向。结果：1.有一平衡位置，该位置的方向定义为磁场方向。单位:特斯拉(T)\n磁感强度的另定义+带电粒子在磁场中运动所受的力与运动方向有关.实验发现带电粒子在磁场中沿某一特定直线方向运动时不受力，此直线方向与电荷无关.+\n带电粒子在磁场中沿其他方向运动时垂直于与特定直线所组成的平面.当带电粒子在磁场中垂直于此特定直线运动时受力最大.大小与无关磁感强度的定义：当正电荷垂直于特定直线运动时，受力将方向定义为该点的的方向.\n单位特斯拉+磁感强度的定义：当正电荷垂直于特定直线运动时，受力将方向定义为该点的的方向.磁感强度大小运动电荷在磁场中受力\n6.3磁力线磁通量磁场中的高斯定理规定：曲线上每一点的切线方向为该点的磁感应强度的方向；曲线的疏密程度表示该点的磁感应强度的大小。III一、磁力线（磁感应强度线）\n磁场中某点处垂直矢量的单位面积上通过的磁力线条数等于该点的大小SNISNI\n二、磁通量磁场的高斯定理磁力线的性质:（1）磁力线是一组无头、无尾的闭合曲线；（2）磁力线与电流的方向相互满足右手螺旋法则。\n磁通量：通过某一曲面的磁力线的条数即为通过此曲面的磁通量。单位韦伯(Wb)\n物理意义：通过任意闭合曲面的磁通量必等于零（磁场是无源的；没有磁单极子）磁场的高斯定理对闭合曲面S：\nP*一、毕奥—萨伐尔定律(电流元在空间产生的磁场)真空磁导率任意载流导线在点P处的磁感强度磁感强度叠加原理6.4毕奥—萨伐尔定律大小方向\n12345678例判断下列各点磁感强度的方向和大小.+++1、5点：3、7点：2、4、6、8点：毕奥—萨伐尔定律\nPCD*例1载流长直导线的磁场.解方向均沿x轴的负方向二毕奥---萨伐尔定律应用举例\n的方向沿x轴的负方向.PCD+讨论电流的方向与磁感强度的方向成右手螺旋关系无限长载流长直导线的磁场IXI\n*P半无限长载流长直导线的磁场电流的方向与磁感强度的方向成右手螺旋关系IXI\n例2如图载流无限长直导线的电流为I,试求通过如图矩形面积的磁通量。解先求，对变磁场给出然后积分求\nI真空中,半径为R的载流导线,通有电流I,称圆电流.求其轴线上一点p的磁感强度的方向和大小.解根据对称性分析例3圆形载流导线的磁场.p*\np*\n3）4）2）的方向不变(和成右螺旋关系）1）若线圈有匝讨论*\no（2R）I+IRo（1）xR（3）oI\noI（5）*Ad（4）*\n++++++++++++pR++*例4载流直螺线管的磁场如图所示，有一长为l,半径为R的载流密绕直螺线管，螺线管单位长度上的匝数为n，通有电流I。求管内轴线上一点处的磁感强度。解由圆形电流磁场公式o\nop+++++++++++++++\n讨论（1）P点位于管内轴线中点若\n(2)对无限长的螺线管由xBO在螺线管内部:在螺线管两端:\n练习1、试求以下各图中圆心处的磁感应强度(图中半径均为R，流入流出电流均为I，各导线是由同种材料制成且粗细均匀)\nl1l2④①②③解：利用得方向⊙方向⊙设园弧l1、l2的电流分别为I1、I2，则有：方向⊙方向\n因所以方向⊙①②③④O同理方向相反方向相反所以\n练习2、在一无限长的半径为R的半圆柱面金属薄片中，自上而下地流有均匀的电流，总的电流强度为I。求：圆柱轴线上任一点的磁感应强度.\n解：将载流圆柱薄壳分成无数多个宽为dl的无限长细导线，则其通有电流：利用：如图所示，因每个方向不同，而由对称性可知dldBxy\n