大学物理习题课

大学物理习题课

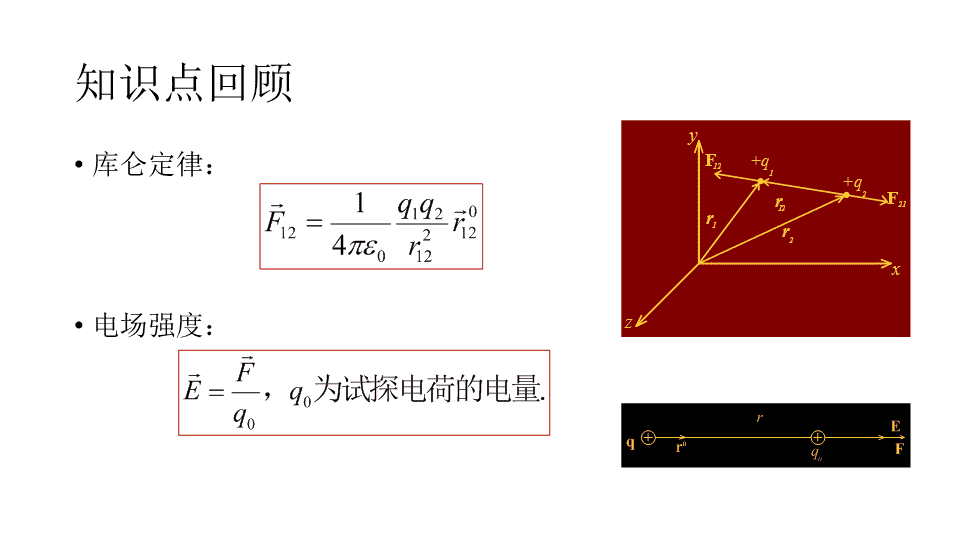
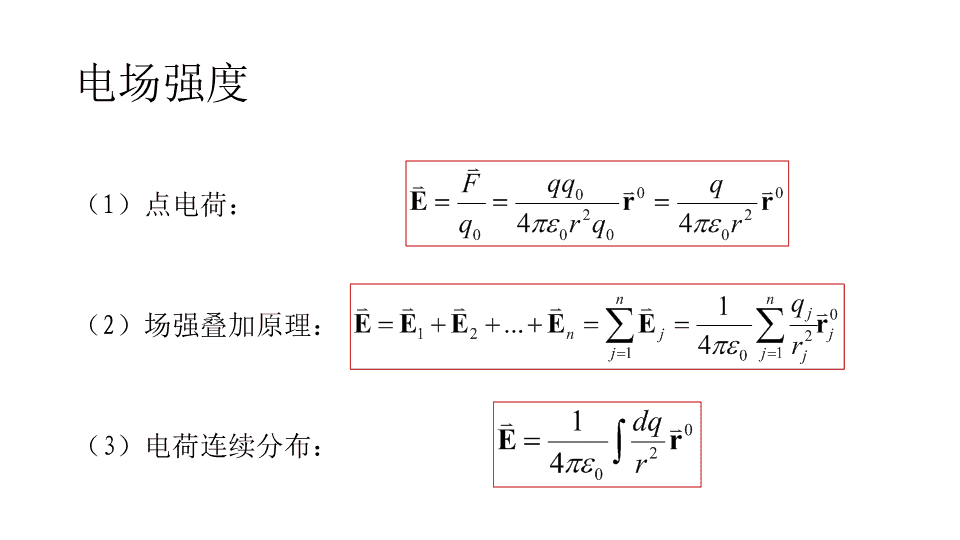
库仑定律：电场强度：知识点回顾\n电场强度（1）点电荷：（2）场强叠加原理：（3）电荷连续分布：\n静电场的高斯定理：通过任意闭合曲面S的电通量Φe，等于该闭合曲面内所有电荷电量的代数和∑q除以ε0，与闭合曲面外的电荷无关。3\n电量都是q的三个点电荷，分别放在正三角形的三个顶点。试问：(1)在这三角形的中心放一个什么样的电荷，就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)?(2)这种平衡与三角形的边长有无关系?FFF’AOBC解：（1）以A处点电荷为研究对象，受力分析：由库仑定理：（2）与边长无关\n解：（1）以中点为原点O，向上为x轴正方向,向右为z轴正方向，在z轴上任取一点P,距离原点为z.(2)细棒上取一电荷单元：(3)电荷单元在P点产生的电场强度为：dE可分解为沿x轴的分量dEx和垂直于z轴分量dEz5例3.设均匀带电细棒长为2l，带电总量为Q。试求细棒中垂面上的场强分布。oPxzdqdEdEzdExθ\noPzdEzdExθdE\nzPrθR一均匀带电薄圆盘，半径为R，电荷面密度为σ.试求：（1）轴线上的场强分布；（2）保持σ不变，若R→0或R→∞,结果如何？（3）保持总电量Q＝πR2σ不变，若R→0或R→∞,结果如何？解：将圆盘分割成许多同心的圆环：该圆环在P点的场强方向沿z轴，大小为：\n因此，P点的总场强积分如下：\n（2）保持σ不变，若R→0，则E＝0；R→∞，即无限大平面的电场强度为：zPrθR\n（3）若保持总电量Q不变，则圆盘的电荷密度为：zPrθR\n解：（1）建立坐标系；（2）选择电荷元；（3）O点的电场强度（4）dE分解为dEx和dEy，由对称性分析可知，y方向上的场强相互抵消dExdEy一个半径为R的均匀带电半圆环，电荷线密度为λ,求环心处O点的场强．\n半径为R的均匀带电球体内的电荷体密度为ρ,若在球内挖去一块半径为r＜R的小球体．试求：两球心O与O’点的场强，并证明小球空腔内的电场是均匀的．解：（1）看作带正电的均匀大球与带负电的均匀小球的组合OO’rRa\n(2)空腔内任取一点P点，O’P为b，OP为rO’OabrP