大学物理课件7

大学物理课件7

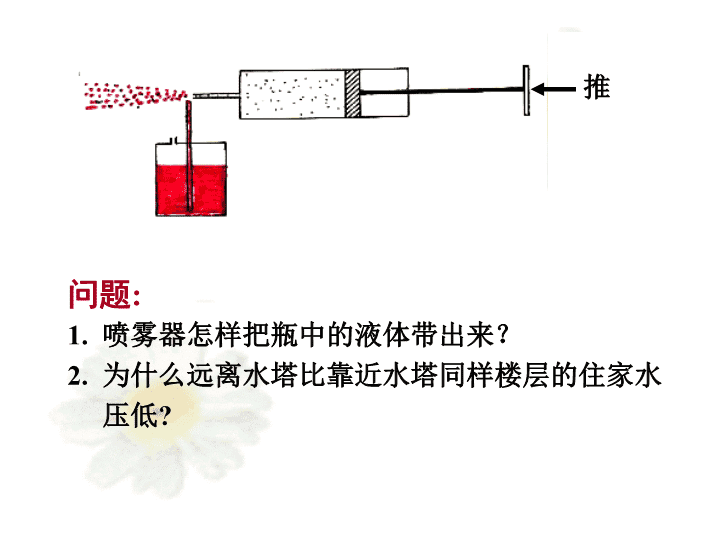
第4章流体运动简介theintroductionofmotionfluid第1节理想流体的运动第2节黏性流体的运动\n航空航天、船舶与海洋——applicationLiftV0G弧旋球船舶运动地效翼艇（WIG）浮标海洋平台潜器\n问题:1.喷雾器怎样把瓶中的液体带出来？2.为什么远离水塔比靠近水塔同样楼层的住家水压低?推\n第1节理想流体的运动themotionofidealfluid一、理想流体的稳定流动实际流体的特性:(1)粘性(viscosity)(2)可压缩性(compressibility)理想流体：绝对不可压缩的、完全没有粘性(或内摩擦力)的流体。1.理想流体(idealfluid)\n2.稳定流动(steadyflow)StudymethodLagrangemethodEulermethod稳定流动时,流速场的空间分布不随时间变化.(1)流速场流体空间中每一点(x,y,z)上有一个速度矢量v(x,y,z),它们构成一个流速场．(2)稳定流动流体在流动时,流体粒子顺序到达空间任一点,而在这一点的速度大小和方向不随时间而改变．两个重要概念：流线和流管\n(3)流线(Streamline)①流线只是一种形象描述;③稳定流动时,流线的分布不随时间改变;②任意两条流线互不相交;④流线与轨迹的关系.?AvABvBCvC\n(4)流管(tubeofflow)①流管同样也是一种形象描述;?②流管的形状在稳定流动时保持不变;③稳定流动时,流管内外的流体彼此互不交换.\n二、连续性方程(continuityequation)1.体积流量:S2S1Sv说明大小流线稀小大流线密2.连续性方程:适用条件:不可压缩的流体作稳定流动.3.质量守恒:S1v1=S2v2单位:m3/sS1v1=S2v2或Sv=CSvtv2v1\n4.分支流管的连续性方程S2S1S3v1v2v3\nBernoulliequation三、伯努利方程及其应用或在流体中同一流管任意两截面处有1738年,英国科学家DanielBernoulli(1700~1782年)利用力学中的功能原理,推导出理想流体在流动中的动力学方程.理想流体作稳定流动时,在流体内同一流管任意点的压强、单位体积势能、单位体积动能满足:\n推导依据:连续性方程和功能原理.\n推导过程：当t→0时(1)假设与近似①aa'处的截面积近似相等(S1)②bb'处的截面积近似相等(S2)③aa'体积内的v1、p1不变,高度h1④bb'体积内的v2、p2不变,高度h2⑤aa'和bb'体积相等V1=V2=V,质量均为m⑥流管周围的流体对流体柱ab的力不做功⑦只有推力F1和阻力F2对流体柱做功\n(2)外力的合力所作的总功A:(3)动能Ek和势能Ep的变化(4)功能原理(work-energytheory)\n(6)方程中各个物理量的单位(5)伯努利方程理想流体作稳定流动时，同一流管的不同截面积处的压强、流体单位体积的势能与单位体积的动能之和都是相等的.静压强动压强\n(7)适用条件①理想流体做稳定流动;②同一流管的不同截面积处或同一流线的不同点;(8)分支管道的伯努利方程:S2S1S3v1v2v3\n(9)特殊情况下方程的简化①不均匀水平管,h1=h2=h②均匀管,S1=S2,v1=v2=v③若某处与大气相通,则该处的压强为大气压p0竖直:水平:\n伯努利方程的应用1.空吸(suction)S2v1p23000,湍流;(3)2000F,加速下降后来:v↑,f↑匀速运动因此:mg=F+f重力浮力黏性阻力(1)定律:固体在黏性流体中运动受到的黏性阻力,实验表明:①v较小,Re<1,f∝l(线度)、v、；②比例系数与固体的形状有关；③球体在沉降过程中所受阻力:f=6rv3.斯托克司定律(StokesLaw)\n(3)收尾速度(terminalvelocity)或沉降速度(sedimentaryvelocity)(4)应用:①沉降法测量流体的黏度；=2gr2()/9v②测量小球的半径（密立根油滴实验）；③离心机的原理；④制造混悬液类的药物时,可以增加悬浮介质的黏度、密度和减小药物颗粒的半径来提高药液的稳定性.v=2gr2()/9\n本章练习第104~106页，4-6、4-11、4-13、4-15、4-16、4-20、4-21、4-24。\n第4章结束\n4-1．流体在同一流管中作稳定流动时，对于不同截面积处的流量是（）A．截面积大处流量大；B．截面积小处流量小；C．截面积大处流量等于截面积小处流量；D．截面积大处流量不等于面积小处流量．4-2．流体在流管中作稳定流动，截面积0.5cm2处的流速为12cm/s。流速4cm/s的地方的截面积是（）A．0.5cm2；B．1.2cm2；C．1.5cm2；D．2.0cm2．本章补充练习\n4-3．理想液体在半径为r的流管中以流速v作稳定流动，将此管与6个并联的半径为r/3的流管接通，则液体在半径为r/3的流管中作稳定流动的流速为（）A．v/6；B．v；C．3v/2；D．v/3．4-4．理想流体在一水平管中做稳定流动时，截面积S、流速v、压强p的关系是（）A．S大处、v小、p大；B．S大处、v大、p大；C．S小处、v大、p小；D．S小处、v小、p小．\n4-5．一个截面积不同的水平管道，在不同的截面积处竖直接两个管状压强计，水不流动时，两压强计中液面高度相同；水流动起来时，压强计中液面怎样变化（将水视为理想流体）（）A．两液面同时升高相等的高度；B．两液面同时下降相等的高度；C．两液面同时下降，但是下降的高度不同；D．两液面都不变化．4-6．一个截面积很大顶端开口的容器，在其底侧面和底部中心各开一个截面积为0.5cm2的小孔，水从容器顶部以200cm3/s的流量注入容器中，则容器中水面的最大高度约为（）A．0.5cm；B．5cm；C．10cm；D．20cm．\n4-7．黏滞流体在半径为r的水平管中流动，其体积流量为Q，如果在半径为r/3的水平管中流动，其它条件不变，则其体积流量为（）A．3Q；B．Q/3；C．81Q；D．Q/81．4-8．粘滞流体通过长度为l、管径为r的流管，流阻为Rf，若再连接长度为l、管径为r/3的流管，则这两段流管的总流阻为（）A．2Rf；B．9Rf；C．10Rf；D．82Rf．