大学物理导体介质2

大学物理导体介质2

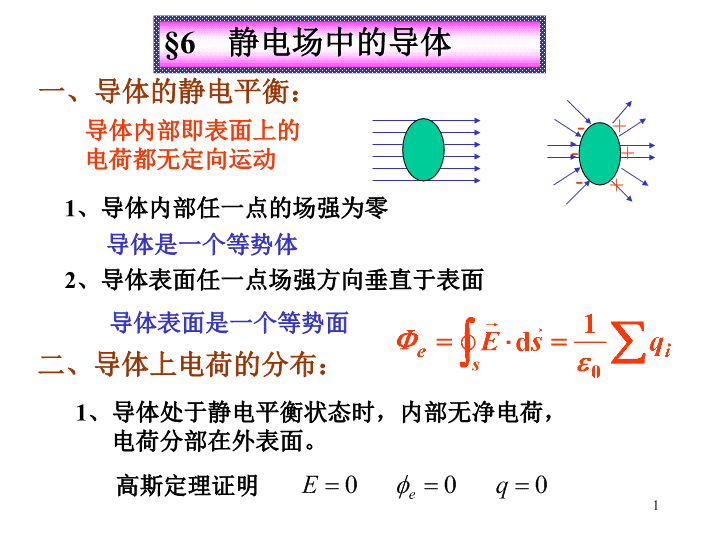
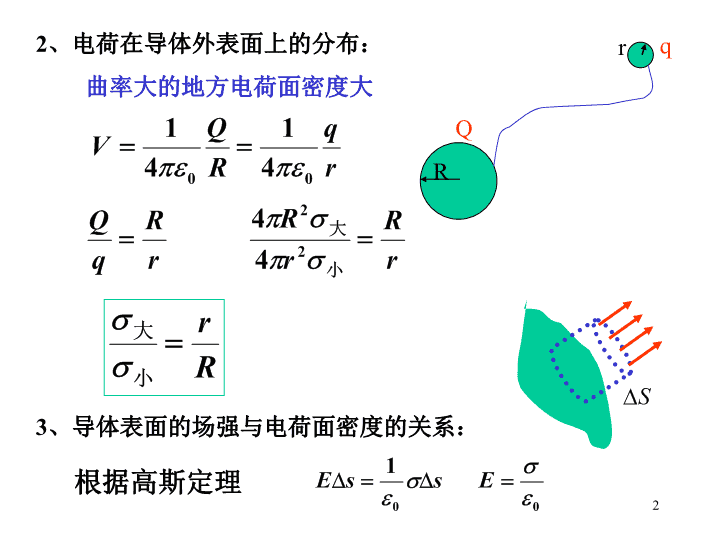
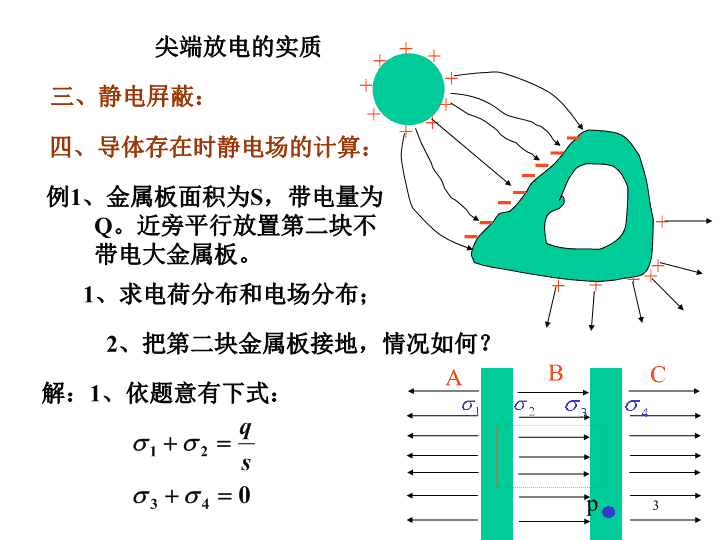
§6静电场中的导体一、导体的静电平衡：导体内部即表面上的电荷都无定向运动1、导体内部任一点的场强为零2、导体表面任一点场强方向垂直于表面导体是一个等势体导体表面是一个等势面二、导体上电荷的分布：1、导体处于静电平衡状态时，内部无净电荷，电荷分部在外表面。高斯定理证明+++---1\n2、电荷在导体外表面上的分布：曲率大的地方电荷面密度大RrQq3、导体表面的场强与电荷面密度的关系：根据高斯定理2\n尖端放电的实质三、静电屛蔽：+++++++++++++++四、导体存在时静电场的计算：例1、金属板面积为S，带电量为Q。近旁平行放置第二块不带电大金属板。1、求电荷分布和电场分布；2、把第二块金属板接地，情况如何？解：1、依题意有下式：pABC3\n选取如图高斯面，根据高斯定理有：图示P点的场强是四个带电面产生的，电场方向朝左方向朝右方向朝右导体表面的场强场强迭加4\n2、右板接地p高斯定理P点的合场强为零ABC5\n例2、点电荷库仑处在导体球壳的中心，壳的内外半径分别为求：1、导体球壳的电势2、离球心处的电势3、把点电荷移开球心，导体球壳的电势是否变化？+q-q+q解：1、2、定义6\n电势迭加3、导体球壳的电势不变，电荷分布不变。7\n五、电容器的电容1、孤立导体球的电容：定义单位2、电容器及其电容：AB平板电容：同轴柱形电容器L8\n同心球形电容器9\n电场电势差电容定义计算电容：10\n3、电容器在电路中的作用：A)、儲存能量，象水库一样。B）、隔直流，通交流。C）、和其他元件组成振荡放大器。4、电容器的串并联：并联：总电容等于各电容器电容之和串联：总电容的倒数是各电容器电容的倒数之和ABAB11\n§7电介质中的静电场一、电介质对电场的影响+++++-----V在平板电容器之间插入一块介质板AB真空无介质，没有物理意义，单位制带来的常数12\n二、介质的极化：+-+-+-+-+-+-+-+-1、无极分子的位移极化：2、有极分子的取向极化E三、极化强度矢量：1、定义单位：2、极化强度矢量与束缚电荷面密度的关系各向同性介质在均匀场里极化n+-p极化电荷面密度为13\n电偶极矩：斜柱体的体积：电极化强度矢量的大小：3、电介质的极化规律，极化率：极化强度矢量与该点的合场强有关，并与介质有关对大多数各向同性电介质比例常数叫做极化率，它与场强无关，与电介质的种类有关，是介质材料的属性。14\n4、极化强度矢量的通量+-+-+-+-+-+-+-+-通量为正，束缚电荷为负+++++介质四、有介质时的高斯定理15\n有介质时的高斯定理电介质中任一闭合曲面的电位移通量等于该面所包围的自由电荷的代数和。电位移线：从正的自由电荷出发，终止于负的自由电荷。电力线：起止于各种正负电荷五、三矢量之间的关系：对大多数各向同性电介质16\n以平板电容为例说明17\n例1、带正电的金属球，半径为R，电量为q，浸在的油中，求电场分布及束缚电荷总量++++++++---解、选取同心高斯封闭球面。r方向自由电荷的场强束缚电荷的场强18\n大小例2、两块金属板间为真空。电荷面密度为，板间电压。保持电量不变，一半空间充以的电介质，板间电压变为多少？束缚电荷面密度多大？+++++++++++--------------+++解、设金属板面积为S间距为d,原电荷密度则、19\n不考滤边缘效应左侧用高斯定理+++++++++++--------------+++等势体1、金属板上电量不变所以20\n板间的电场强度有介质时的电压2、束缚电荷面密度21\n8电荷在外电场中的静电势能电荷在静电场中移动时，它的静电势能的减少就等于电场力所做的功。功与电位差的关系电荷在电场中某点的电势能等于它的电量与电场中该点电势的乘积电势能是电荷和产生电场的电荷系所共有的例：求电矩的电偶极子在均匀外电场中的电势能。22\nAB-q+q解：正负电荷的电势能分别为矢量式P与E方向一致时，W最小P与E方向相反时，W最大P与E垂直时，W为零23\n9电荷系的静电能将各电荷从现有位置彼此分散到无限远时，它们之间的静电力所做的功定义为电荷系在原来状态的静电能。也称相互作用能（互能）。1、两个点电荷：间距为r,带电量分别为和。搬动到无限远电场力做功所在点由所产生的电势也可以写作r24\n写成对称形式2、三个电荷：搬动做功25\n3、n个点电荷电荷系带电体26\n例：一均匀带电球体，半径为R，带电量为q。求带电球体的静电能。解、场强分布Rr0球壳的电势27\n28\n10电场的能量一、以平板电容为例计算能量+++++设平板电容器的带电过程是不断搬动电荷元从负板到正板的过程电荷电压能量初态：000中间态qu终态QUW29\n场能密度：适用于任何电场场能密度的单位:任何电场的总能量30\n例、计算球形电容器的总能量解：两球间的电场强度31\n1、计算电容器电容的改变量。2、铜板位置对结果是否有影响？例、空气平板电容器，极板面积为S，间距为d，今以厚度为的铜板平行地插入电容器内。3、充电到电势差为后断开电源，抽出铜板作功多少？+++++解：1、铜板插入前的电容设极板带电为32\n3、电容器充电到电势差为U时，极板带电量为切断电源抽出铜板电容器所储能量为储能33\n例：一均匀带电球体，半径为R，带电量为q。求带电球体的静电能。解、场强分布Rr034\n电荷在外电场中的电势能偶极子在外电场中的静电能电荷系的静电能静电场的能量35