大学物理10-213148

大学物理10-213148

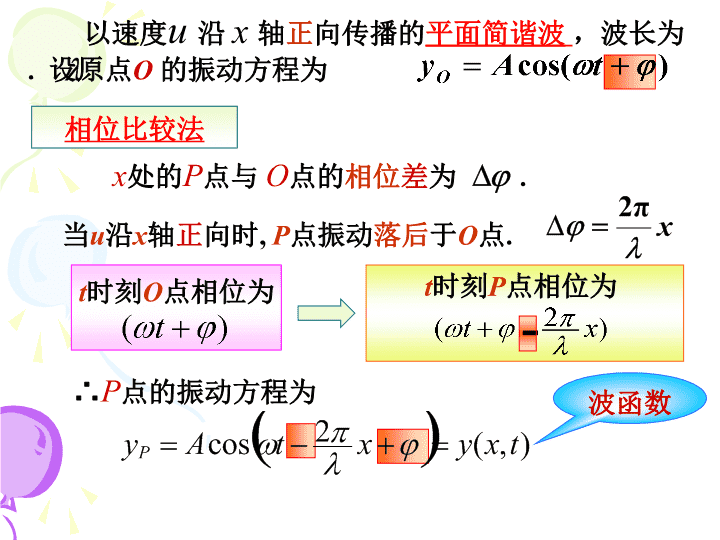
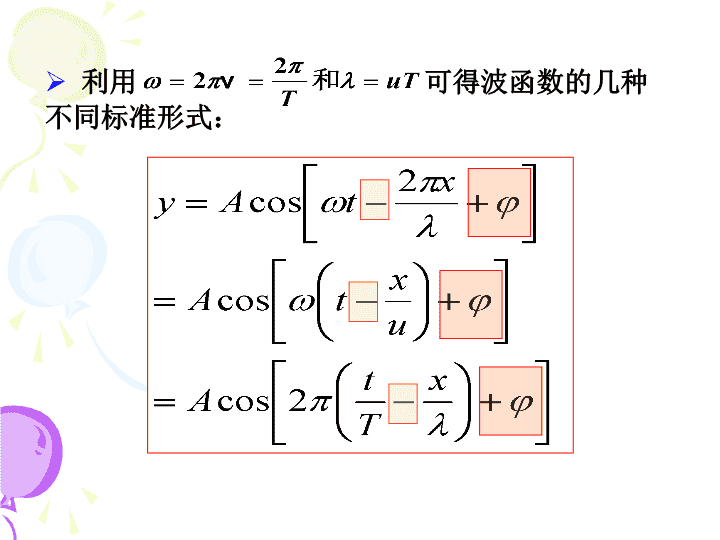
§10-2平面简谐波的波函数一平面简谐波的波函数（波动方程）介质中任一质点（坐标为x）相对其平衡位置的位移（坐标为y）随时间t的变化关系，即y=y(x，t)称为波函数.简谐波：在均匀的、无吸收的介质中，波源作简谐运动时，在介质中所形成的波.简谐波介质中各质元均作简谐振动.平面简谐波：波面为平面的简谐波.各质点相对平衡位置的位移波线上各质点平衡位置\n以速度u沿x轴正向传播的平面简谐波，波长为.设原点O的振动方程为∴P点的振动方程为波函数相位比较法x处的P点与O点的相位差为.当u沿x轴正向时,P点振动落后于O点.t时刻O点相位为t时刻P点相位为相位比较法得波函数\n利用可得波函数的几种不同标准形式：波函数的几种标准形式\n二波函数的物理意义1.若x=x0一定，t变化（常数）表示x0点处质点的振动方程.（y-t的关系）令则yOt\n该方程表示t0时刻波传播方向上各质点的位移,即t0时刻的波形.（y-x的关系）令2.若t＝t0一定，x变化则（定值）yOx2.若t＝t0一定，x变化\n波函数表示在不同时刻各质点的位移或不同时刻的波形，体现了波形的传播（行波）.3.若x、t都变化.O时刻O时刻时刻3.若x、t都变化\n质点的振动速度，振动加速度分别为：沿x轴正方向传播的波函数标准方程质点的振动速度，振动加速度方程\n4.沿x轴负方向传播的波动方程P点振动比O点超前了如图，设O点振动方程为故P点的振动方程为：此即为左行波的波函数4.沿x轴负方向传播的波动方程OxxPuy\nOxy5.若O点为真正的波源P’P到O点距离相等的P和P’点振动都落后于O点设O点振动方程为故任一x处质点的振动方程为：波函数\n1）波动方程例1(P53)一平面简谐波沿Ox轴正方向传播，已知振幅，，.在时坐标原点处的质点位于平衡位置沿Oy轴正方向运动.求解写出波动方程的标准式O\n2）求时各质点的位移，并做波形图.波形方程o2.01.0-1.0时刻波形图\n3）处质点的振动规律并做图.处质点的振动方程01.0-1.02.0O1234******1234处质点的振动曲线1.0\n1）以A为坐标原点，写出波动方程ABCD5m9m8m解设波动方程为：由原点A的运动方程知：例31）以A为坐标原点，写出波动方程例2(P53)一平面简谐波以速度沿直线传播,波线上点A的简谐运动方程(SI).\nABCD5m9m8m2）以B为坐标原点O’，写出波动方程解：由代入B坐标，得即2）以B为坐标原点O’，写出波动方程\n3）写出传播方向上点C、点D的简谐运动方程ABCD5m9m8m解：点C的相位比点A超前点D的相位落后于点A3）写出传播方向上点C、点D的简谐运动方程\n解：由相位差与波程差之间的关系求得4）分别求出BC，CD两点间的相位差ABCD5m9m8m4）分别求出BC，CD两点间的相位差\n1）判断下列波函数所表示的波的传播方向和点的初相位.2）平面简谐波的波函数为式中为正常数，求波长、波速、波传播方向上相距为的两点间的相位差.讨论向x轴正向传播向x轴负向传播对比讨论\nOabct=T/43）如图简谐波以余弦函数表示，求O、a、b、c各点振动初相位.t=0OOOO3）求O、a、b、c各点振动初相位.