大学物理稳恒磁场

大学物理稳恒磁场

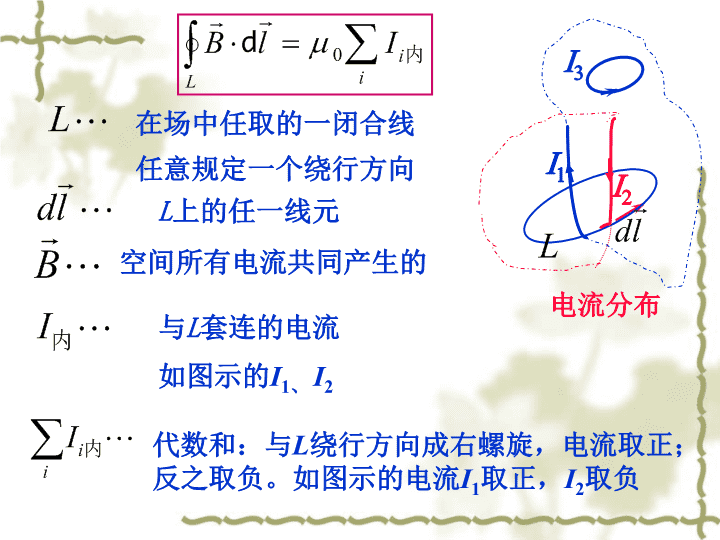
一、安培环路定理电磁规律比较：§4安培环路定理及应用表述：在稳恒电流的磁场中，磁感应强度沿任何闭合路径L的线积分，等于路径L所包围的电流强度的代数和的倍。\n空间所有电流共同产生的在场中任取的一闭合线任意规定一个绕行方向L上的任一线元与L套连的电流如图示的I1、I2代数和：与L绕行方向成右螺旋，电流取正；反之取负。如图示的电流I1取正，I2取负电流分布I2I1I3\n讨论1）安培环路定理只适用于闭合恒定电流,是稳恒电流磁场的性质方程。（对一段恒定电流的磁场，或变化电流的磁场不成立）2）说明磁场为非保守场（涡旋场）3）积分中为空间所有的稳恒电流共同激发的。但其沿环路的积分却只与环路所包围的电流有关。\n[C]\n如图，流出屏幕的电流为2I，流进屏幕的电流为I，则下述各式中那一个是正确的?(B)(A)[D](C)(D)\n二、安培环路定理在解场方面的应用对于一些对称分布的电流可以通过取合适的环路L利用磁场的环路定理比较方便地求解场量(类似于电场强度的高斯定理的解题)以例题说明解题过程\n设总匝数为N、总长为L分析对称性，知内部场沿轴向，方向与电流成右手螺旋关系1.通电密绕长直螺线管内部的磁感强度通过稳恒电流电流强度为I螺线管均匀密绕无漏磁\n取过场点的每个边都相当小的矩形环路abcda由安培环路定理均匀场\n2.无限长通电流I的圆柱导体内外的B磁场特点：方向沿圆周切向同一圆周上各点B大小相等、I取回路：过场点的圆周，绕行方向与I成右螺旋设圆柱体截面半径为Rrrpp则有轴对称性\nrrIppRBr无限长圆柱导体电流外面的磁场与电流都集中在轴上的直线电流的磁场相同\nrprpRBr无限长通电柱面I思考：有人说：“环路不环绕电流时，环路上磁场必处处为零，对吗？\n通电环形螺线管磁场的磁感线\n3.均匀密绕螺绕环设通有的电流强度为I，总匝数为N磁场特点：方向沿圆周切向同一圆周上各点B大小相等、取回路：过场点的圆周，绕行方向与I成右螺旋场点距中心的距离r\n外部：以rR2为半径作圆形安培回路L，得外部磁场分布在细螺绕环的情形下，其内部的磁感强度大小处处相等，但各处的方向并不相同，故不是均匀磁场。对细螺绕环\n例:无限大平板电流的磁场分布。设一无限大导体薄平板垂直于纸面放置，其上有方向垂直于纸面朝外的电流通过，面电流密度（即指通过与电流方向垂直的单位长度的电流）到处均匀。大小为解：视为无限多平行长直电流的场。分析场点p的对称性因为电流平面是无限大，故与电流平面等距离的各点B的大小相等。在该平面两侧的磁场方向相反。\n作一安培回路如图：bc和da两边被电流平面等分。ab和cd与电流平面平行,则有在无限大均匀平面电流的两侧的磁场都为均匀磁场，并且大小相等，但方向相反。方向如图所示。\n电流(线)密度为j的无限大均匀载流平面,在其两侧产生大小相等、方向相反的匀强磁场j·······BB结果\n基本方法：1.利用毕－萨－拉定律2.某些对称分布，利用安培环路定理3.重要的是典型场的叠加注意与静电场对比磁感强度的计算\n一无限长任意导线中通以电流I，有人运用安培环路定律计算空间P点的磁感应强度，由，得到，与无限长载流直导线的磁场一样。这样处理对吗？思考\n磁通量：穿过磁场中某一面的磁力线条数单位：1Wb（韦伯）=1Tm2例1.RB\n例.载流长直导线的电流为I，它与一矩形共面，试求通过该矩形的磁通量？Iaxbhx\nIhcdI\n例．一无限长圆柱形铜导体（磁导率μ0)，半径为R，通有均匀分布的电流I，今取一矩形平面S（长为1m，宽为2R），位置如图所示，求通过该矩形平面的磁通量。\n\n例一长直电流I在平面内被弯成如图所示的形状其中直电流ab和cd的延长线过o电流bc是以o为圆心、以R2为半径的1/4圆弧电流de也是以o为圆心、但，是以R1为半径的1/4圆弧直电流ef与圆弧电流de在e点相切求：场点o处的磁感强度\n解：场点o处的磁感强度是由五段特殊形状电流产生的场的叠加，即由毕萨拉定律得到各电流的磁感强度分别是方向：\n例.一半径为R2带电薄圆盘,其中半径为R1的阴影部分均匀带正电荷,面电荷密度为+,其余部分均匀带负电荷,面电荷密度为–,当圆盘以角速度旋转时,测得圆盘中心点o的磁感应强度为零,问R1与R2满足什么关系？解：当带电圆盘转动时,可看作无数个圆电流的磁场在o点的迭加,\n半径为r,宽为dr的圆电流dI=2rdr/2=rdr磁场dB=0dI/2r=0dr/2阴影部分产生的磁场感应强度为其余部分：十七章作业：2\n例2：在截面均匀铜环上任意两点用两根长直导线沿半径方向引到很远的电源上,求：环中心处o点的磁感应强度。解：如图所示的电流系统在o点激发的B为5段电流所产生的B矢量的迭加。o点在直电流IAE与IFB所在延长线上。又O点离IEF很远，此电流的磁场可不计。\nI1电流在O点的磁场：I2电流在O点的磁场：\n又R1和R2并联,故有R1I1=R2I2由电阻定理知,ACB和ADB的电阻R1和R2与其长度L1和L2间有\n1.电流由直导线1沿平行bc边方向经过点a流入一电阻均匀分布的正三角形线框,再由b点沿cb方向流出，经长直导线2返回电源(如图).已知直导线上的电流为I,三角框的每一边长为l，令长直导线1、2和导线框在线框中心点O产生的磁感应强度分别为B1、B2和B3则点O的磁感应强度大小:\n[D]十七章作业：9\n2.边长为l的正方形线圈中通有电流,此线圈在A点（见图）产生的磁感应强度B为[A]①③②④\n3．一载有电流I的细导线分别均匀密绕在半径为R和r的长直圆筒上形成两个螺线管(R=2r)，两螺线管单位长度上的匝数相等．两螺线管中的磁感应强度大小BR和Br应满足：[B]\n4.两半径为R的相同导体细圆环,互相垂直放置,且两接触点A、B连线为环的直径,现有电流1沿AB连线方向由A端流入,再由B端流出,则环中心处的磁感应强度大小为:[A](A)0(C)(B)(D)(E)\n5.如图所示，电流由长直导线1经a点流入电阻均匀分布的正方形线框，再由b点流出，经长直导线2返回电源（导线1、2的延长线均通过o点）。设载流导线1、2和正方形线框在框中心o点产生的磁感应强度分别用B1、B2、B3表示，则o点的感应强度大小\n（D）B0，因为虽然B3=0，但B1+B20（C）B0，因为虽然B1+B2=0，但B30（B）B=0，因为虽然B10、B20、B30，但B1+B2+B3=0。（A）B=0，因为B1=B2=B3=0。[A]\n6.有一边长为l电阻均匀分布的正三角形导线框abc，与电源相连的长直导线1和2彼此平行并分别与导线框在a点和b点相接，导线1和线框的ac边的延长线重合。导线1和2的电流为I，如图所示。令长直导线1、2和导线框在线框中心点o产生的磁感应强度分别为B1、B2和B3，则点o的磁感应强度大小：\n[D]\n7.取一闭合积分回路L，使三根载流导线穿过它所围成的面．现改变三根导线之间的相互间隔，但不越出积分回路，则[B](A)回路L内的I不变，L上各点的B不变．(B)回路L内的I不变，L上各点的B改变.(C)回路L内的I改变，L上各点的B不变.(D)回路L内的I改变，L上各点的B改变.